nLab AdS-QCD correspondence
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
Contents
- Idea
- Polyakov gauge/string duality
- Models
- Top-down models
- Bottom-up models
- Comparison with experiment
- Embedding into the standard model of particle physics
- Related concepts
- References
- Polyakov gauge/string duality
- General
- Hadrons as KK-modes of 5d Yang-Mills theory
- Hadron physics
- Baryons as instantons
- Baryons as wrapped branes
- Baryons as Skyrmions
- Nucleons
- Pentaquarks
- Parton distribution functions
- Heavy flavor in holographic QCD
- Flux string breaking
- Glueball physics
- Holographic Schwinger effect
- Application to vector meson dominance
- Application to the quark-gluon plasma
- Application to lepton anomalous magnetic moment
- Application to the Higgs field
- Application to -angle axions and strong CP-problem
- Application to the QCD trace anomaly
- Application to parton distribution
- Application to QCD phases
- Application to meson physics
- Application of holographic QCD to B-meson physics and flavour anomalies
- Relation to holographic entanglement entropy
- Application to defects
- Application to thermal QCD
Idea
What is called holographic QCD or AdS/QCD correspondence or similar (review includes Aharony 02, Erlich 09, Kim-Yi 11, Erlich 14, Rebhan 14, Rho-Zahed 16) is a quantitatively predictive model for quantum chromodynamics (“QCD”, the strong nuclear force-sector of the standard model of particle physics) via “holography” (as in the AdS/CFT correspondence), hence regarding it as the boundary field theory of an (at least) 5-dimensional Yang-Mills theory (“bottom-up holographic QCD”), specifically one geometrically engineered on intersecting D-branes (“top-down holographic QCD”) and here specifically on D4-D8 brane intersections (the Witten-Sakai-Sugimoto model due to Witten 98, Karch-Katz 02, Sakai-Sugimoto 04, Sakai-Sugimoto 05).
While QCD, taken at face value, is not a quantum field theory of the kind considered in the plain AdS-CFT correspondence – since it is not a conformal field theory (but see KPV22) and not supersymmetric (hence not an SCFT, but see at hadron supersymmetry) and does not have a large number of colors (but see below), it is thought that approximations/deformations of AdS-CFT may still usefully apply.
Holographic QCD captures the non-perturbative confined regime of QCD, which is otherwise elusive (the Mass Gap Millennium Problem), where the would-be quarks are all bound/confined inside color-less hadrons, with the meson fields instead being the gauge field of a flavour-gauge theory (holographic dictionary, e.g. Kim-Yi 11 (3.1), see also “hidden local symmetry”) and the baryons being solitons of this flavour/meson field, namely skyrmions.
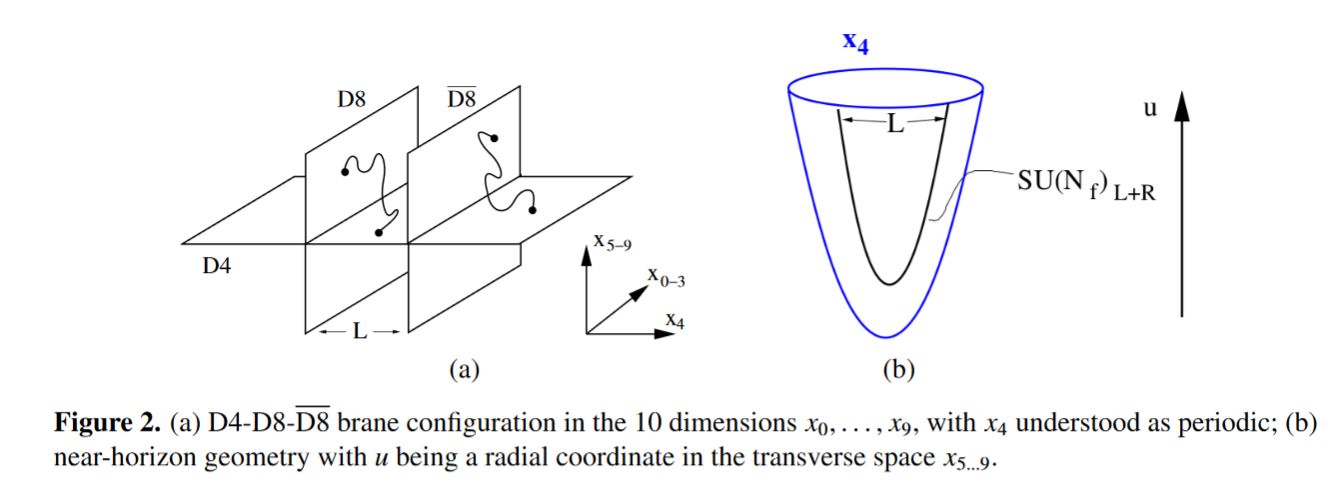
This dual description of the color gauge theory of quarks and gluons instead as flavour gauge theory of baryons and mesons is geometrically brought out by the D4-D8 brane intersections of the Witten-Sakai-Sugimoto intersecting D-brane model: Here the open strings on the D4 color branes give the color/gluon gauge field, while those on the D8 flavor branes give the flavour/meson gauge field, those stretching between D4 and D8 give the quarks and the closed strings give the glueballs. (See at WSS brane configuration below.) This way color/flavor duality is mapped to open/closed string duality (as the D8-branes are treated as probe branes).
Notice that the flavour sector is where most of the open problems regarding the standard model of particle physics are located (flavour problem, flavour anomalies).
Various fundamental characteristics of QCD that remain mysterious in the colored-quark model readily find a conceptual explanation in terms of this geometric engineering of flavour physics, notably the phenomena of confinement and of chiral symmetry breaking, but also for instance vector meson dominance and the Cheshire cat principle.
Indeed, holographic QCD gives accurate quantitative predictions of confined hadron spectra, hence of the physics of ordinary atomic nuclei (see comparison between experiment and predictions of holographic QCD below) which is out of reach for perturbation theory and otherwise computable, at best, via the blind numerics of lattice QCD. This means (Witten 98) that holographic QCD provides a conceptual solution to the mass gap problem (not yet a rigorous proof, but a proof strategy).
Concretely, much of the phenomenological success of holographic QCD is (review in Rho-Zahed 16, Chapter III) due to the holographic emergence of the time-honored but ad hoc Skyrmion-model of baryons, as solitons in the meson flavour-gauge field.

Moreover, in holographic QCD this Skyrmion model of baryons emerges in its modern improved form, where the pion field is accompanied by the whole tower of vector mesons (the rho meson etc.): these meson species are holographically unified as the transversal KK-modes in the holographic theory. Already just adjoining the rho meson to the pion makes the resulting Skyrmions, and hence holographic QCD, give accurate results for light nuclei all the way up to carbon (Naya-Sutcliffe 18a, Naya-Sutcliffe 18b).
The mechanism behind this description of baryons and nuclei via holographic QCD is the theorem of Atiyah-Manton 89 (highlighted as such in Sutcliffe 10) which identifies Skyrmions in 3+1-dimensional Yang-Mills theory with KK modes (transversal holonomies) of instantons in 4+1-dimensional YM theory:
This fact (of experiment/phenomenology on the left and of mathematics on the right) combined with the emergence of strings in the 't Hooft limit of QCD reveals a de facto holographic nature of QCD. The task in holographic QCD is to sort out the fine-print.
A key open problem here is that the AdS/CFT correspondence is currently well understood only in the large N limit, where the number of colors and the 't Hooft coupling are both large. But for QCD the number of colors is small, . While the correspondence is thought to hold also in the small N limit, here the classical super-gravity-computations on the dual (AdS) side will receive small-N corrections (highlighted for holographic QCD e.g. in Sugimoto 16, see references below) from perturbative string theory (for small 't Hooft coupling) which are hard to compute, and then from M-theory (for small ) which are largely unknown, as formulating M-theory remains an open problem. Hence from the perspective of small-N corrected holographic QCD, the mass gap problem/confinement problem translates to the problem of formulating M-theory:
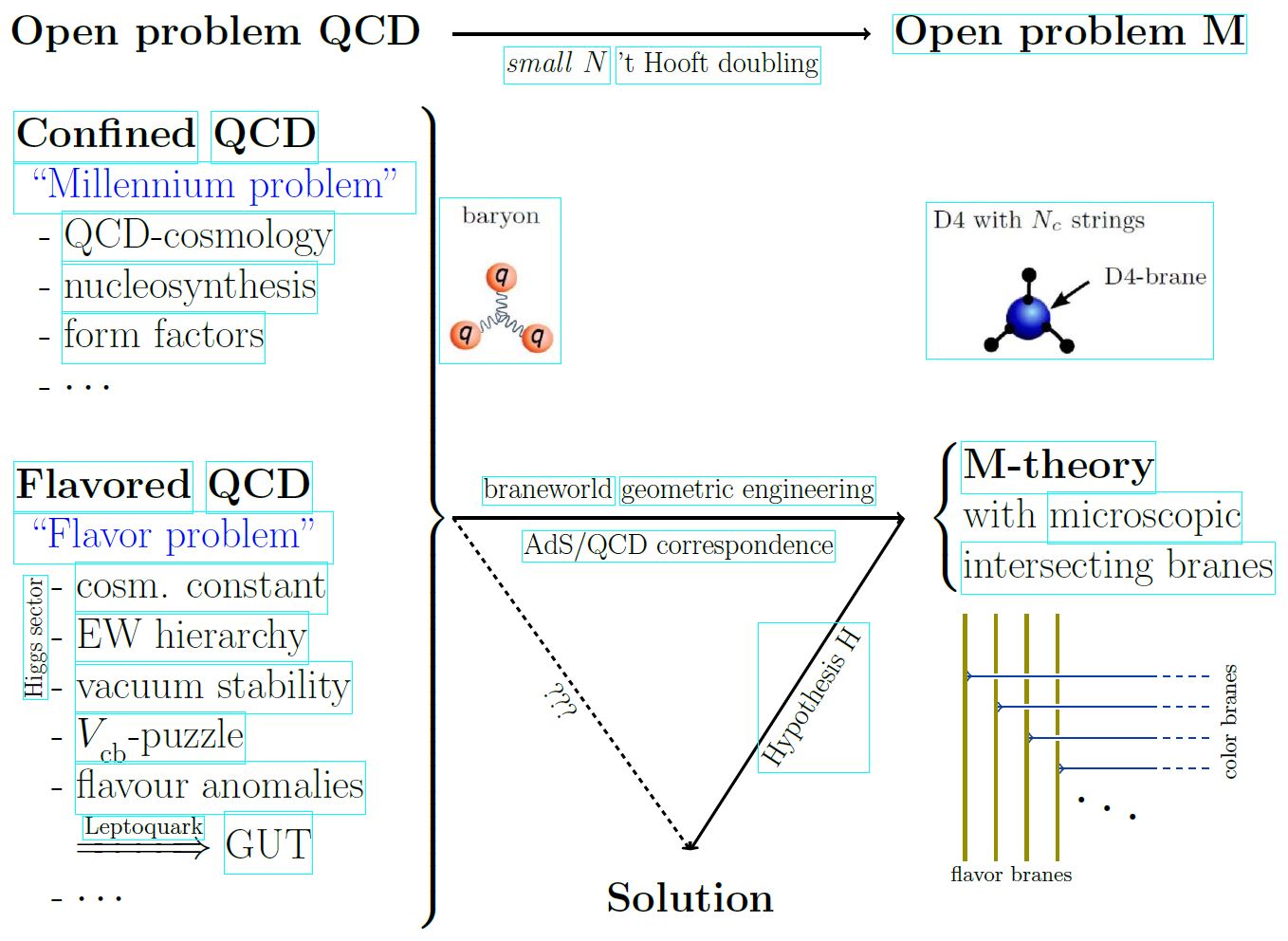
From Yi 09:
QCD is a challenging theory. Its most interesting aspects, namely the confinement of color and the chiral symmetry breaking, have defied all analytical approaches. While there are now many data accumulated from the lattice gauge theory, the methodology falls well short of giving us insights on how one may understand these phenomena analytically, nor does it give us a systematic way of obtaining a low energy theory of QCD below the confinement scale.
it has been proposed early on that baryons are topological solitons, namely Skyrmions but the usual Skyrmion picture of the baryon has to be modified significantly in the context of full QCD.
the holographic picture naturally brings a gauge principle in the bulk description of the flavor dynamics in such a way that all spin one mesons as well as pions would enter the skyrmionic-construction of baryons on the equal footing.
holographic QCD is similar to the chiral perturbation theory in the sense that we deal with exclusively gauge-invariant operators of the theory. The huge difference is, however, that this new approach tends to treat all gauge-invariant objects together. Not only the light meson fields like pions but also heavy vector mesons and baryons appear together, at least in principle. In other words, a holographic QCD deals with all color-singlets simultaneously, giving us a lot more predictive power.
The expectation that there exists a more intelligent theory consisting only of gauge-invariant objects in the large Nc limit is thus realized via string theory in a somewhat surprising manner that the master fields, those truly physical degrees of freedom, actually live not in four dimensional Minkowskian world but in five or higher dimensional curved geometry. This is not however completely unanticipated, and was heralded in the celebrated work by Eguchi and Kawai in early 1980’s which is all the more remarkable in retrospect.
To compare against actual QCD, we must fix the 't Hooft coupling and the KK-scale to fit both the pion decay constant and the mass of the first vector meson. After this fitting, all other infinite number of masses and coupling constants are fixed. This version the holographic WSS model of the holographic QCD is extremely predictive.
this elevates the classic Skyrme picture based on pions to a unified model involving all spin one mesons in addition to pions. This is why the picture is extremely predictive.
As we saw in this note, for low momentum processes, such as soft pion processes, soft rho meson exchanges, and soft elastic scattering of photons, the holographic WSS-model’s predictions compare extremely well with experimental data. It is somewhat mysterious that the baryon sector works out almost as well as the meson sector
From Suganuma-Nakagawa-Matsumoto 16, p. 1:
Since 1973, quantum chromodynamics (QCD) has been established as the fundamental theory of the strong interaction. Nevertheless, it is very difficult to solve QCD directly in an analytical manner, and many effective models of QCD have been used instead of QCD, but most models cannot be derived from QCD and its connection to QCD is unclear.
To analyze nonperturbative QCD, the lattice QCD Monte Carlo simulation has been also used as a first-principle calculation of the strong interaction. However, it has several weak points. For example, the state information (e.g. the wave function) is severely limited, because lattice QCD is based on the path-integral formalism. Also, it is difficult to take the chiral limit, because zero-mass pions require infinite volume lattices. There appears a notorious “sign problem” at finite density.
On the other hand, holographic QCD has a direct connection to QCD, and can be derived from QCD in some limit. In fact, holographic QCD is equivalent to infrared QCD in large Nc and strong 't Hooft coupling , via gauge/gravity correspondence. Remarkably, holographic QCD is successful to reproduce many hadron phenomenology such as vector meson dominance, the KSRF relation, hidden local symmetry, the GSW model and the Skyrme soliton picture. Unlike lattice QCD simulations, holographic QCD is usually formulated in the chiral limit, and does not have the sign problem at finite density.
From Rho et a. 16:
One can make chiral perturbation theory consistent with QCD by suitably matching the correlators of the effective theory to those of QCD at a scale near . Clearly this procedure is not limited to only one set of vector mesons; in fact, one can readily generalize it to an infinite number of hidden gauge fields in an effective Lagrangian. In so doing, it turns out that a fifth dimension is “deconstructed” in a (4+1)-dimensional (or 5D) Yang–Mills type form. We will see in Part III that such a structure arises, top-down, in string theory.
this holographic QCD model comes out to describe — unexpectedly well — low-energy properties of both mesons and baryons, in particular those properties reliably described in quenched lattice QCD simulations.
One of the most noticeable results of this holographic model is the first derivation of vector dominance (VD) that holds both for mesons and for baryons. It has been somewhat of an oddity and a puzzle that Sakurai's vector dominance — with the lowest vector mesons ρ and ω — which held very well for pionic form factors at low momentum transfers famously failed for nucleon form factors. In this holographic model, the VD comes out automatically for both the pion and the nucleon provided that the infinite KK-tower is included. While the VD for the pion with the infinite tower is not surprising given the successful Sakurai VD, that the VD holds also for the nucleons is highly nontrivial. It turns out to be a consequence of a holographic Cheshire Cat phenomenon
Polyakov gauge/string duality
Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical reminiscences in Polyakov (2008)) under the name gauge/string duality, in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings.
The logic here proceeds in the following steps (cf. Polyakov (2007), §1 and see the commentary below):
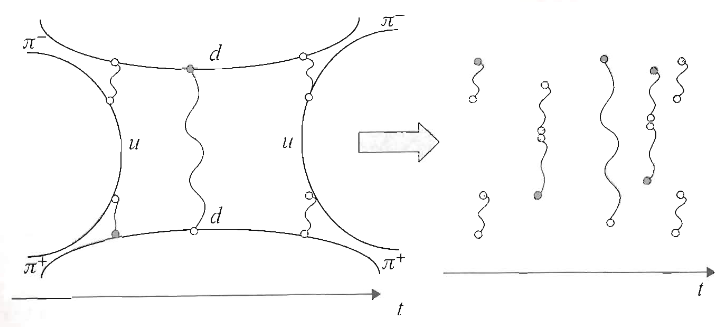
-
flux tubes confine as dynamical strings
The starting point is the hypothesis that the strong coupling of particles (such as quarks) by a (non-abelian) gauge field (such as the strong nuclear force) is embodied by the formation of “flux tubes” (“Wilson lines”) between pairs of such particles, which in themselves behave like strings with a given tension.
Kogut & Susskind (1974), (1975); Wilson (1974); Polyakov (1979), (1980), (1987); Makeenko & Migdal (1981), following Nambu (1970), Gotō (1971)
Under this assumption it would be:
-
the flux tube/string‘s tension which keeps the particles at theirs endpoints confined,
-
the excitation of these flux tubes/strings which follow Regge trajectories (such as of hadrons);
-
the scattering of these flux tubes/strings which explains the observed Veneziano amplitudes,
which are the main qualitative features to be explained.
-
-
quantum flux tubes probe effective higher dimensions
But if so, famous quantum effects make such flux tubes/strings behave like propagating in an effective/emergent higher-dimensional spacetime:
-
either because one regards the string as a priori propagating in non-critical spacetime-dimension , in which case the dilaton field/Liouville field appears to cancel the quantum anomaly and acts like a warped 5th dimension:
this was the point of view published in Polyakov (1981) but later claimed, in Polyakov (2008), to have originated already “by the end of ‘77”;
-
or because one regards the string as propagating in critical dimension (10 for the superstring) right away,
which is the point of view adopted later in AdS-CFT duality, starting with Maldacena (1997)
with only the endpoints of the flux tube/string constrained to lie in the original lower dimensional spacetime
which now appears (in modern language that Polyakov did not originally use) as a “brane” inside a higher dimensional bulk spacetime.
Notice that in this picture the observable physics that we set out to describe takes place on the brane (underlying which is typically flat Minkowski spacetime!) at the asymptotic boundary of a higher-dimensional bulk spacetime, while the (potentially large) extra dimensions of a possibly AdS-bulk remain primarily unobservable. In fact, in Polyakov’s original picture the extra 5th dimension is not so much a spacetime dimension but a parameter for the thickness of the flux tube, which becomes non-vanishing due to quantum effects cf. Polyakov (2008), p. 3.
-
-
large/small confined gauge theory is holographic string theory/M-theory
Thus the description of strongly coupled matter via flux tubes/strings now reveals a holographic situation where strongly-coupled quantum fields on intersecting branes are equivalently described by a theory of quantum gravity mediated by strings propagating in a higher dimensional bulk spacetime.
In relation to gauge string duality this is due to Gubser, Klebanov & Polyakov (1998), which is now understood as part of AdS/CFT duality, but it is actually meant to be more general, cf. Polyakov & Rychkov (2000).
While this dual bulk string theory is itself strongly-coupled unless the “number of coincident branes” is humongous (the “large-N limit”) and thus unrealistic after all, the difference is that recognizing the branes as physical objects reveals a web of concrete hints as to the string’s strongly-coupled (non-perturbative) completion, going under the working title M-theory, cf. at AdS-CFT – Small corrections.
In summary, the plausible approach of understanding strongly-coupled quantum gauge theories by regarding their flux tubes as dynamical strings seems to recast the Millennium Problem of understanding strongly-coupled matter into the problem of formulating M-theory: Given M-theory, it ought to be possible to find intersecting brane models of single (or a small number of coincident) M-branes (such as the Witten-Sakai-Sugimoto model M5-brane system) on whose worldvolume the desired strongly-coupled field theory is realized (such as QCD).
Notice the decisive early insight of Alexander Polyakov here: While the idea that strings somehow describe hadronic bound states was the very origin of string theory in the early 1970s (“dual resonance models”), the mainstream abandoned this perspective in the later 1970s when the critical dimension and the full spectrum of the string became fully understood (cf. Goddard-Thorn no-ghost theorem) and declared that instead string should be understood as a grand unified theory of everything including quantum gravity (see e.g. the historical review of Veneziano (2012), esp. pp. 30-31 which still clings to this perspective). From here it was only through the long detour of first discovering, inside this grander theory: D-branes (and M5-branes) in the 1990s, then their near-horizon AdS-CFT duality just before the 2000s and then another decade of exploring intersecting D-brane models that the community in the 2010s came back full circle to Polyakov’s holographic perspective on QCD, now dubbed holographic QCD, in which strings are flux tubes that propagate not (alone) in the observable 4 spacetime dimensions but in a primarily unobservable (meanwhile known as Randall-Sundrum-like) higher-dimensional bulk spacetime – a holographic description of reality that Polyakov (1999) referred to as the wall of the cave, in allusion to Plato (cf. also Polyakov (2008), p. 6).
Our whereabouts in this remarkable picture are still often misunderstood today: If string theory is a theory of nature, then, it seems, we see the wall but not the cave: we live on a Minkowskian brane intersection at the (asympotic) boundary of a primarily unobserved anti de Sitter bulk – which may better be thought of not as physical space but as a configuration space of quantum flux.
Models
In approaches to one distinguishes top-down model building – where the ambition is to first set up a globally consistent ambient intersecting D-brane model where a Yang-Mills theory at least similar to QCD arises on suitable D-branes (geometric engineering of gauge theories) – from bottom-up model building approaches which are more cavalier about global consistency and first focus on accurately fitting the intended phenomenology of QCD as the asymptotic boundary field theory of gravity+gauge theory on some anti de Sitter spacetime. (Eventually both these approaches should meet “in the middle” to produce a model which is both realistic as well as globally consistent as a string vacuum; see also at string phenomenology.)
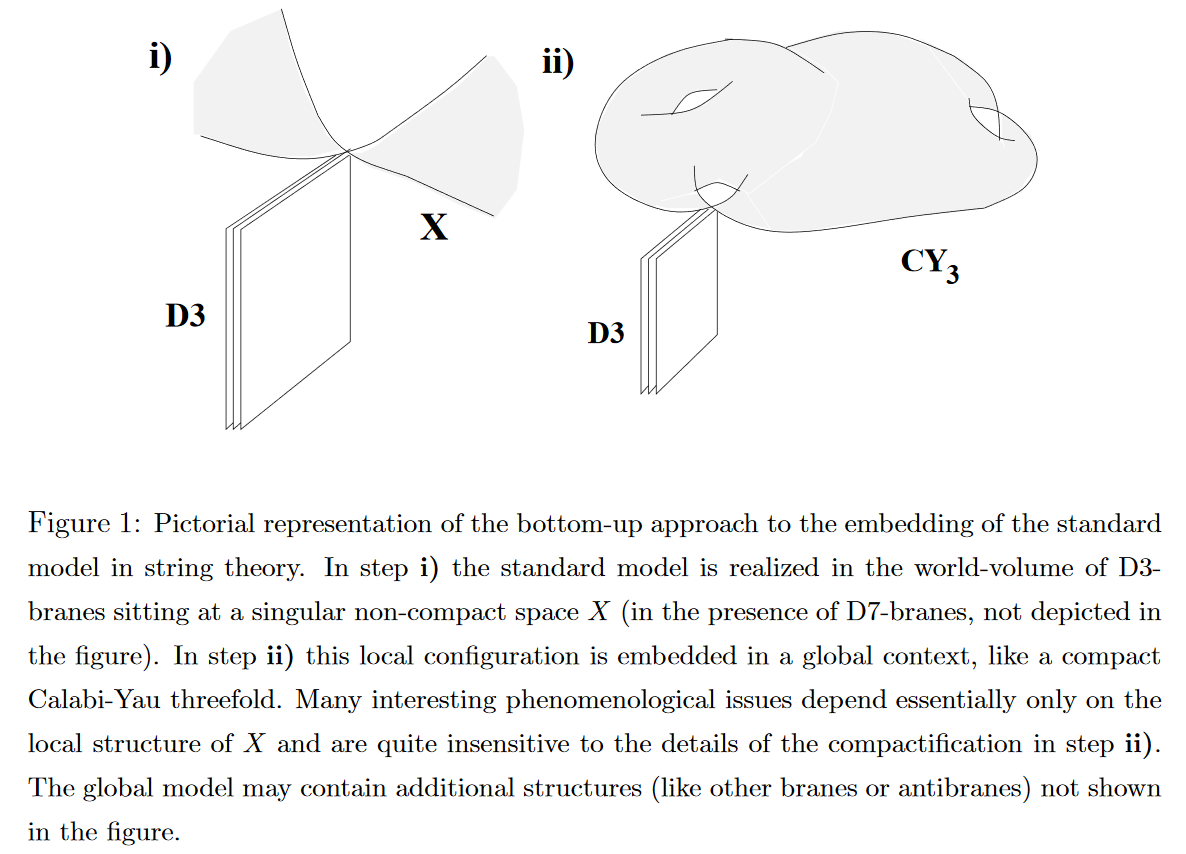
graphics from Aldazabal-Ibáñez-Quevedo-Uranga 00
Top-down models
Witten-Sakai-Sugimoto model
A good top-down model building-approach to AdS/QCD is due to Sakai-Sugimoto 04, Sakai-Sugimoto 05 based on Witten 98, see Rebhan 14, Sugimoto 16 for review.
Brane configuration
The Witten-Sakai-Sugimoto model geometrically engineers something at least close to QCD: on the worldvolume of coincident black M5-branes with near horizon geometry a KK-compactification of in the decoupling limit where the worldvolume theory becomes the 6d (2,0)-superconformal SCFT. Here the KK-compactification is on a torus with anti-periodic boundary conditions for the fermions in one direction, thus breaking all supersymmetry (Scherk-Schwarz mechanism). Here the first circle reduction realizes, under duality between M-theory and type IIA string theory, the M5-branes as D4-branes, hence the model now looks like 5d Yang-Mills theory further compactified on a circle. (Witten 98, section 4).
The further introduction of intersecting D8-branes and anti D8-branes to D4-D8 brane bound states makes a sensible sector of chiral fermions appear in this model (Sakai-Sugimoto 04, Sakai-Sugimoto 05)
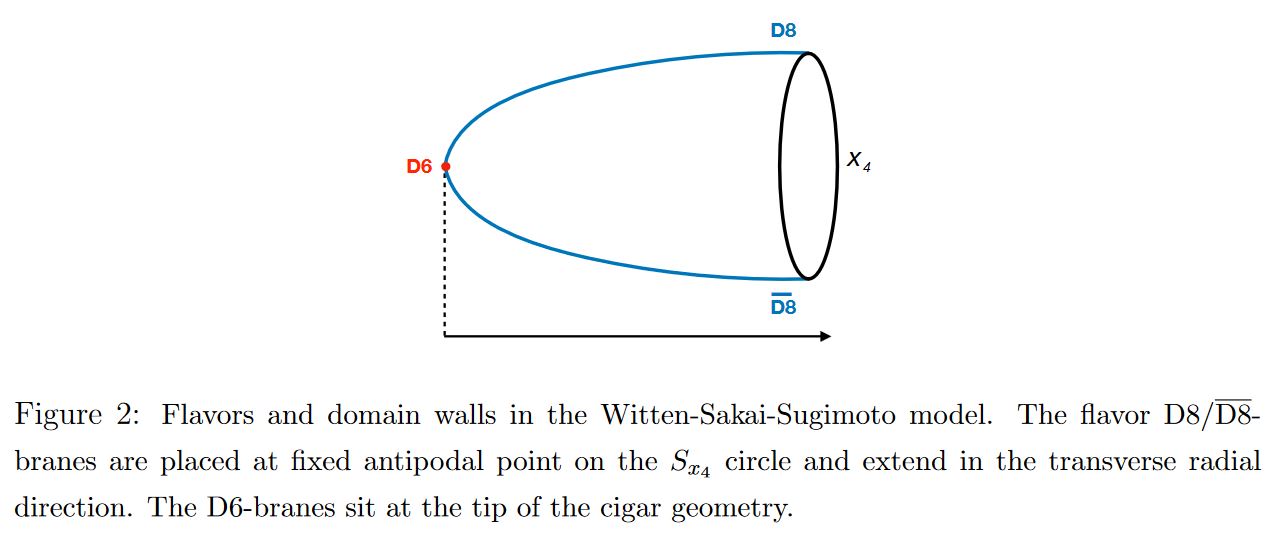
The following diagram indicates the Witten-Sakai-Sugimoto intersecting D-brane model that geometrically engineers QCD:
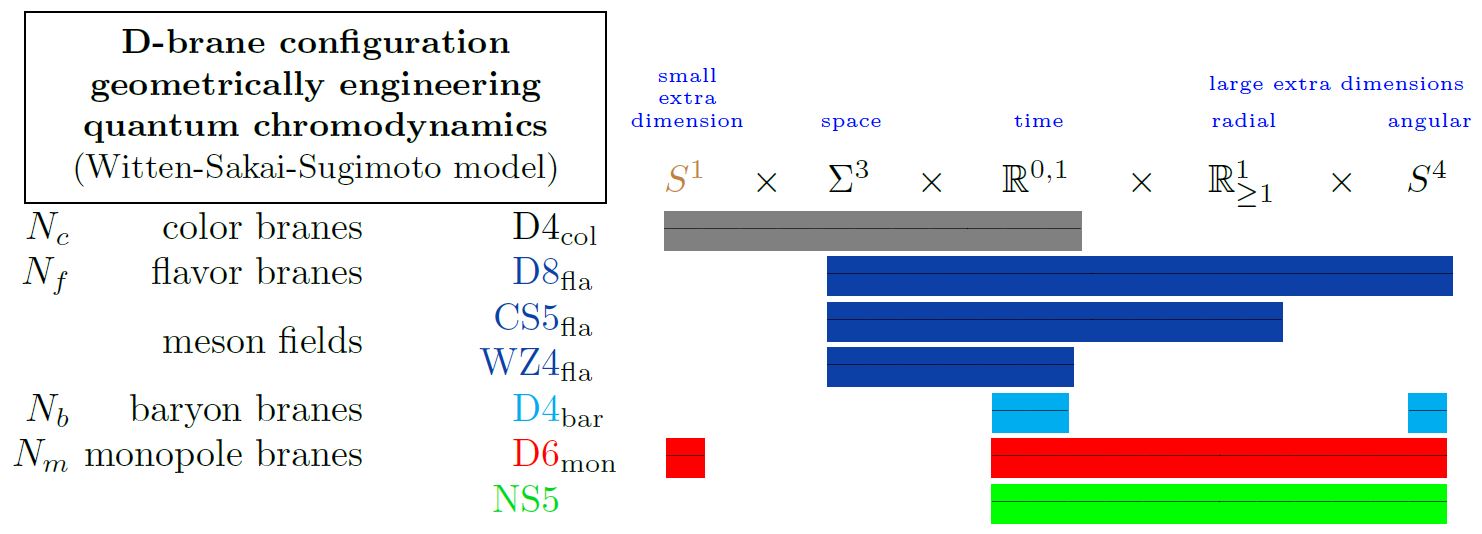
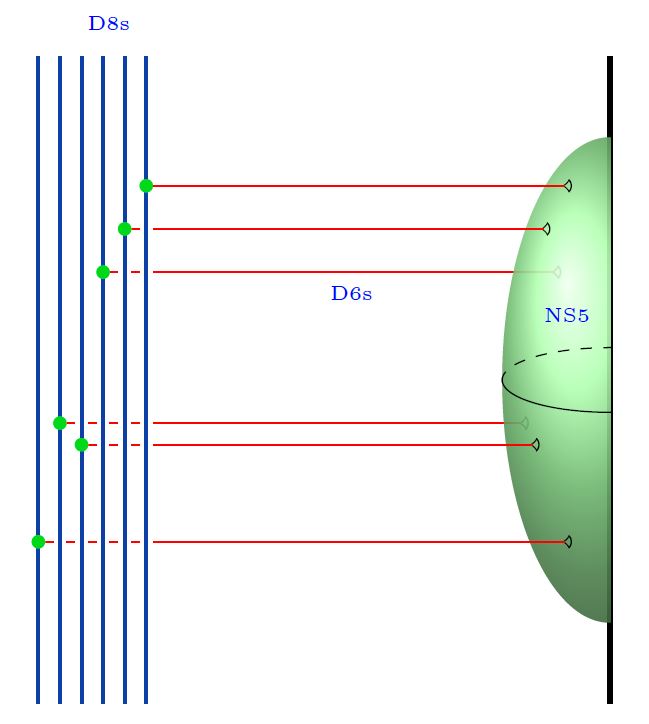
graphics from Sati-Schreiber 19c
Here we are showing:
-
with
-
the 5d Chern-Simons theory on their worldvolume
-
the corresponding 4d WZW model on the boundary
exhibiting the vector meson fields in the Skyrmion model;
-
-
(see below at Baryons);
-
the Yang-Mills monopole D6-branes
(see at D6-D8-brane bound state);
-
the NS5-branes (often not considered here).
graphics from Sati-Schreiber 19c
Glueballs
Already before adding the D8-branes (hence already in the pure Witten model) this produces a pure Yang-Mills theory whose glueball-spectra may usefully be compared to those of QCD:
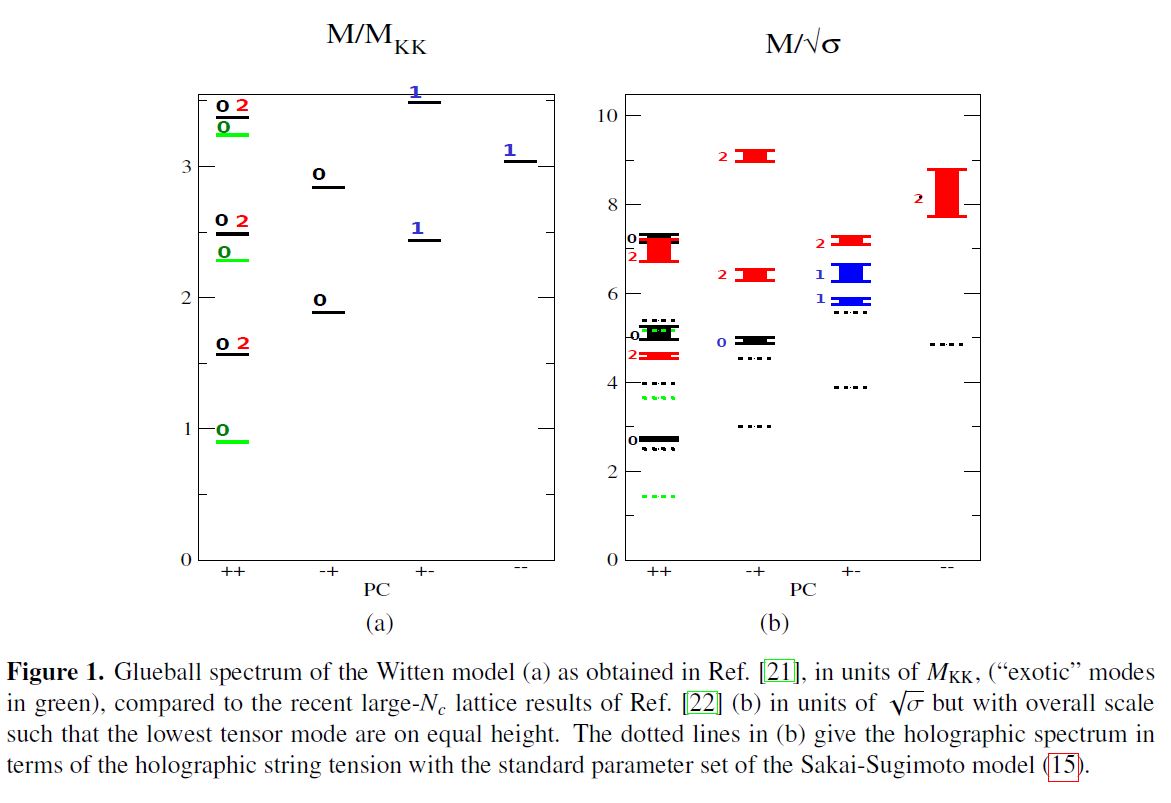
graphics from Rebhan 14
Hadrons
In this Witten-Sakai-Sugimoto model for strongly coupled QCD the hadrons in QCD correspond to string-theoretic-phenomena in the bulk field theory:
Mesons
The mesons (bound states of 2 quarks) correspond to open strings in the bulk, whose two endpoints on the asymptotic boundary correspond to the two quarks
Baryons
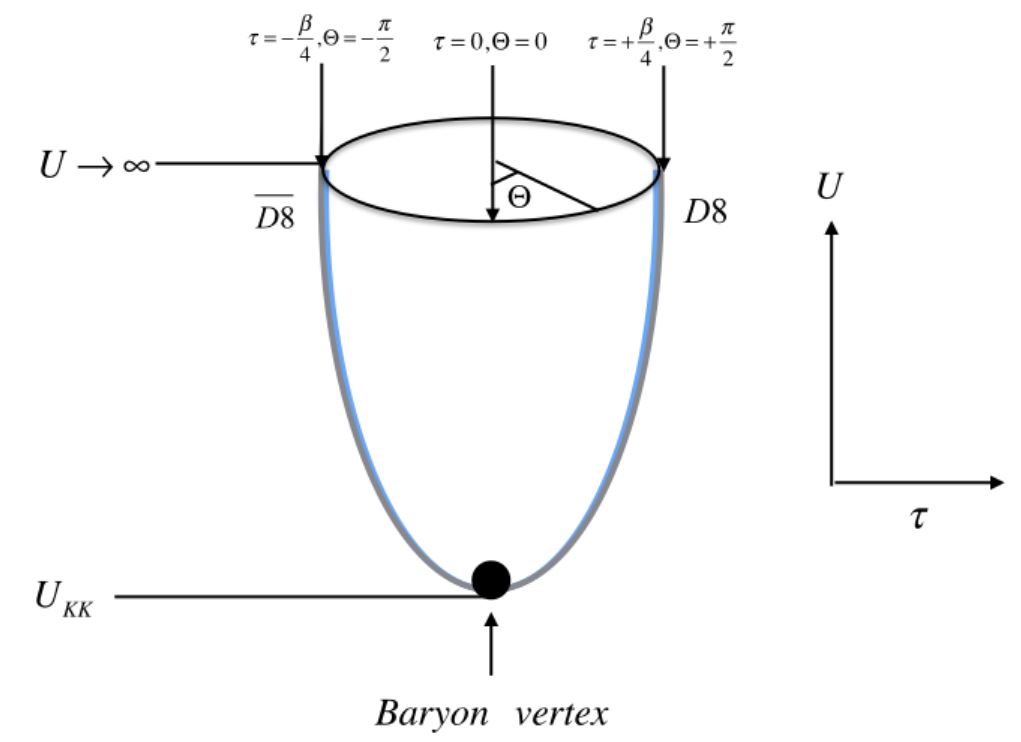
The baryons (bound states of quarks) appear in two different but equivalent (Sugimoto 16, 15.4.1) guises:
-
as wrapped D4-branes with open strings connecting them to the D8-brane
-
as skyrmions
(Sakai-Sugimoto 04, section 5.2, Sakai-Sugimoto 05, section 3.3, see Bartolini 17).
For review see Sugimoto 16, Yi 09, Yi 11, Yi 13, also Rebhan 14, around (18).
graphics from Sugimoto 16
Equivalently, these baryon states are the Yang-Mills instantons on the D8-brane giving the D4-D8 brane bound state (Sakai-Sugimoto 04, 5.7) as a special case of the general situation for Dp-D(p+4)-brane bound states (e.g. Tong 05, 1.4).
graphics from Cai-Li 17
graphics from ABBCN 18
This already produces baryon mass spectra with moderate quantitative agreement with experiment (HSSY 07):
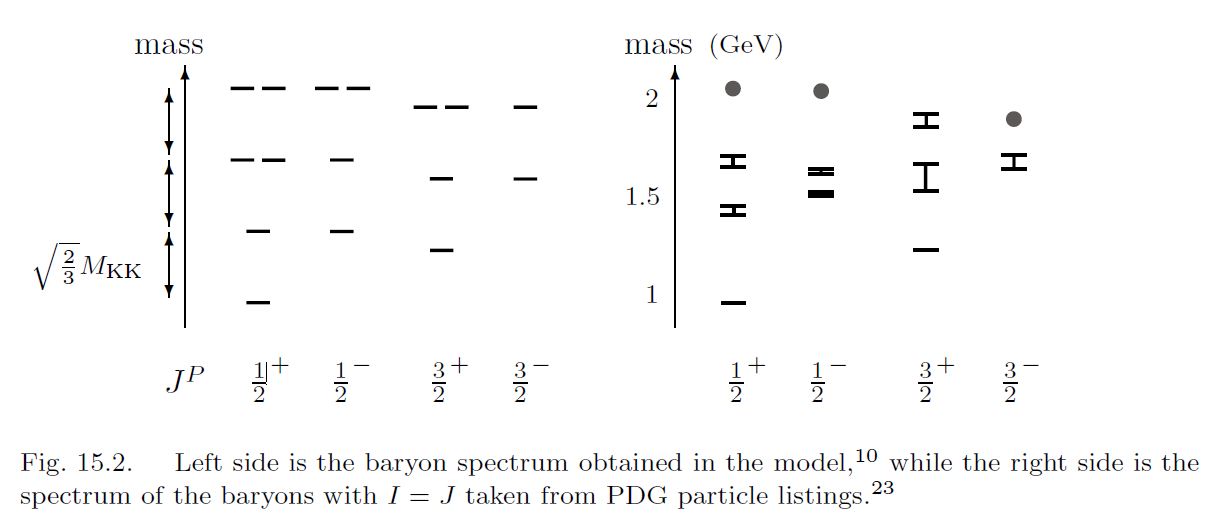
graphics from Sugimoto 16
Moreover, the above 4-brane model for baryons is claimed to be equivalent to the old Skyrmion model (see Sakai-Sugimoto 04, section 5.2, Sakai-Sugimoto 05, section 3.3, Sugimoto 16, 15.4.1, Bartolini 17).
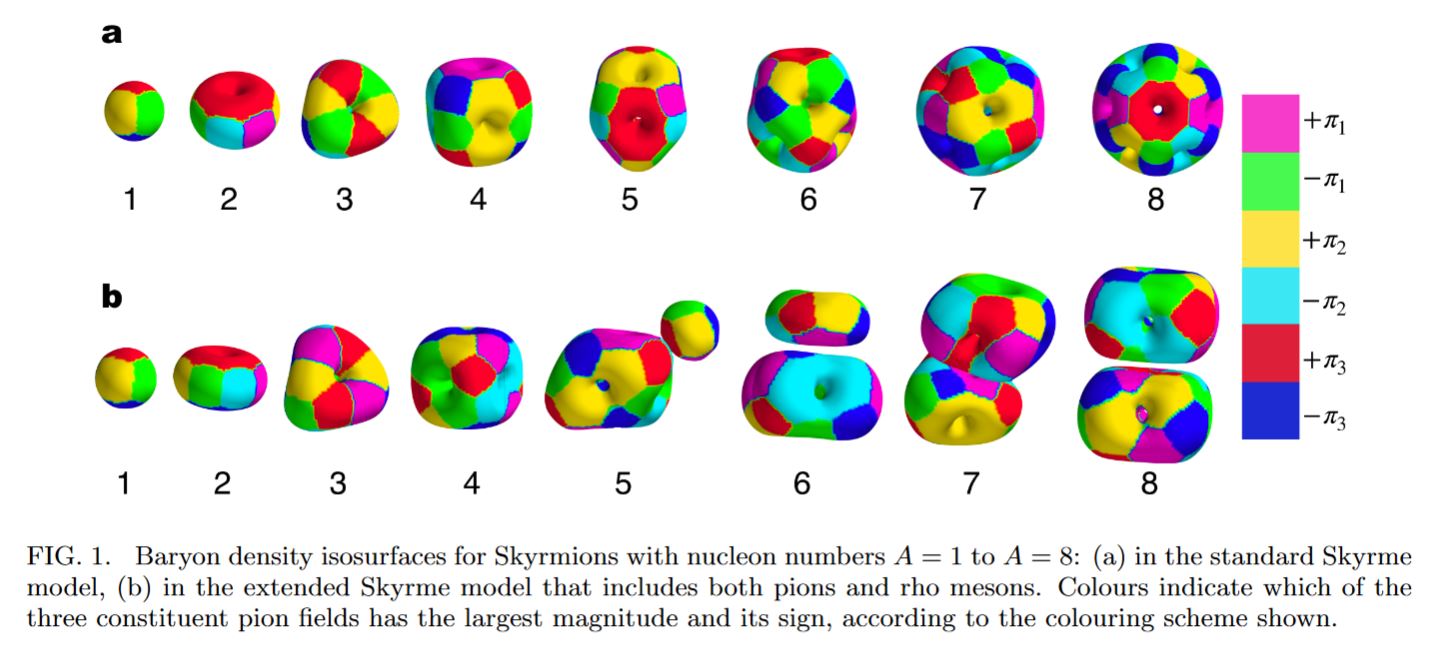
But the Skyrmion model of baryons has been shown to apply also to bound states of baryons, namely the atomic nuclei (Riska 93, Battye-Manton-Sutcliffe 10, Manton 16, Naya-Sutcliffe 18), at least for small atomic number.
For instance, various experimentally observed resonances of the carbon nucleus are modeled well by a Skyrmion with atomic number 6 and hence baryon number 12 (Lau-Manton 14):

graphics form Lau-Manton 14
More generally, the Skyrmion-model of atomic nuclei gives good matches with experiment if not just the pi meson but also the rho meson-background is included (Naya-Sutcliffe 18):
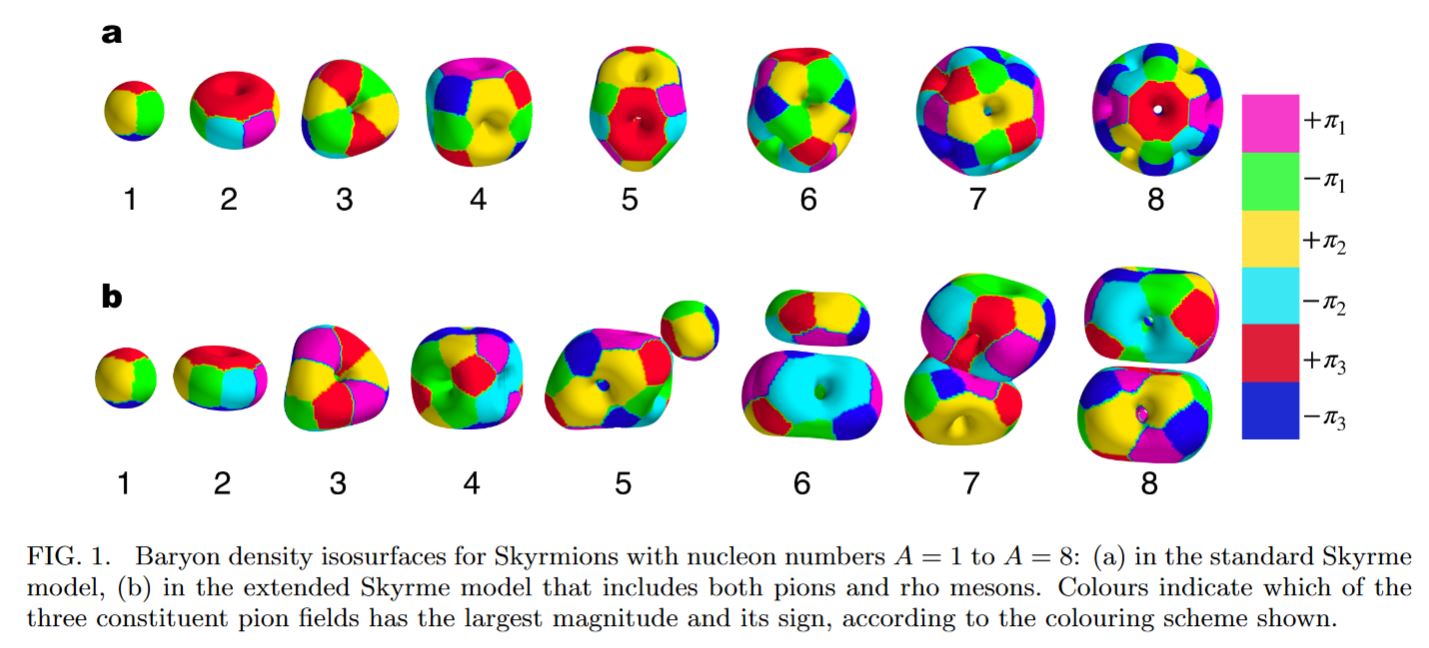
graphics form Naya-Sutcliffe 18
WSS-type model for 2d QCD
There is a direct analogue for 2d QCD of the above WSS model for 4d QCD (Gao-Xu-Zeng 06, Yee-Zahed 11).
The corresponding intersecting D-brane model is much as that for 4d QCD above, just with
-
meson fields given by 3d Chern-Simons theory instead of 5d Chern-Simons theory:

Type0B/-correspondence
Instead of starting with M5-branes in locally supersymmetric M-theory and then spontaneously breaking all supersymmetry by suitable KK-compactification as in the Witten-Sakai-Sugimoto model, one may start with a non-supersymmetric bulk string theory in the first place.
In this vein, it has been argued in GLMR 00 that there is holographic duality between type 0 string theory and non-supersymmetric 4d Yang-Mills theory (hence potentially something close to QCD). See also AAS 19.
Bottom-up models
A popular bottom-up approach of AdS/QCD is known as the hard-wall model (Erlich-Katz-Son-Stephanov 05).
Further refinement to the “soft-wall model” is due to KKSS 06 and further to “improved holographic QCD” is due to Gursoy-Kiritsis-Nitti 07, Gursoy-Kiritsis 08, see GKMMN 10.
Comparison with experiment
Comparison of holographic QCD models with experiment (mostly using bottom-up models).
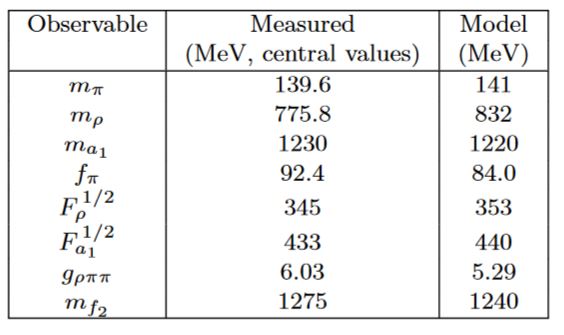
Computations due to Katz-Lewandowski-Schwartz 05 using the hard-wall model (Erlich-Katz-Son-Stephanov 05) find the following comparison of AdS/QCD predictions to QCD-experiment
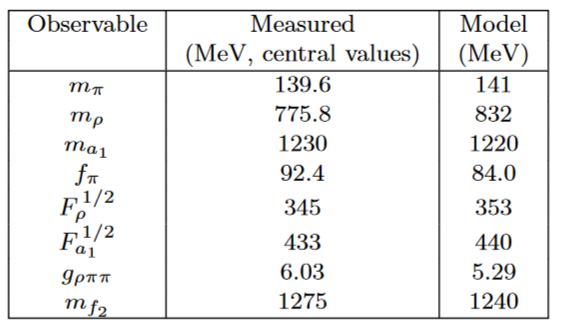
graphics from Erlich 09, section 1.2
Computations due to KKSS 06, Gursoy-Kiritsis-Nitti 07, Gursoy-Kiritsis 08, see GKMMN 10:

graphics from GKMMN 10
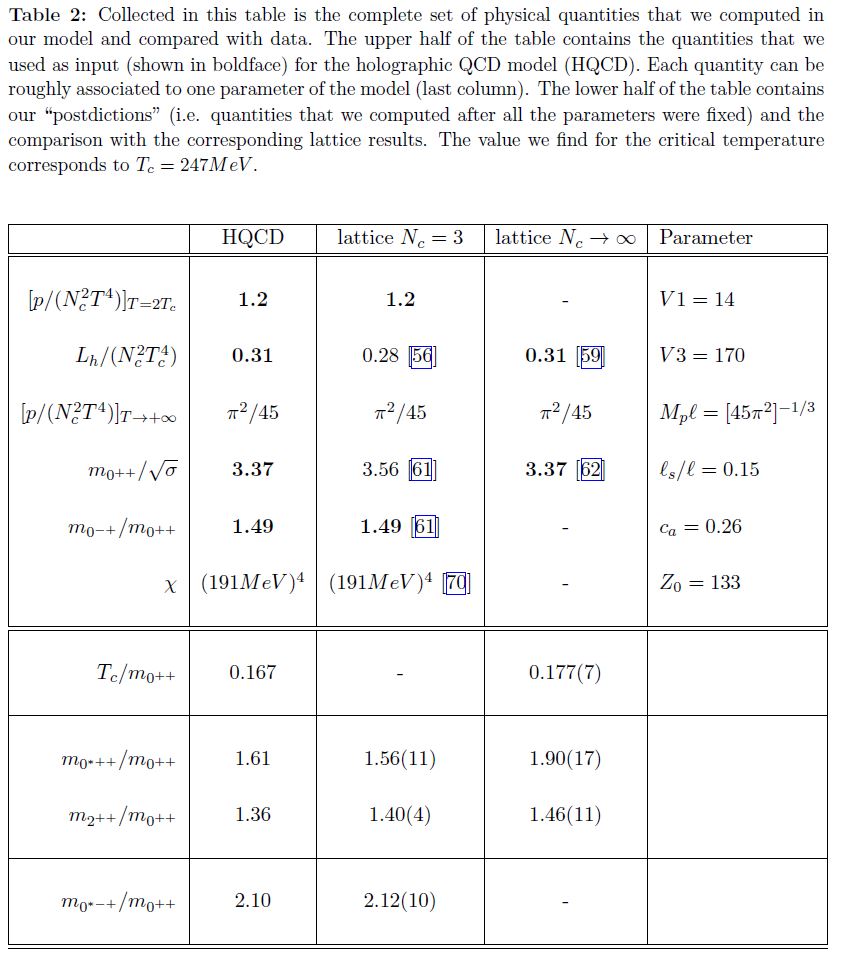
graphics from GKMMN 10
From Pomarol-Wulzer 09:
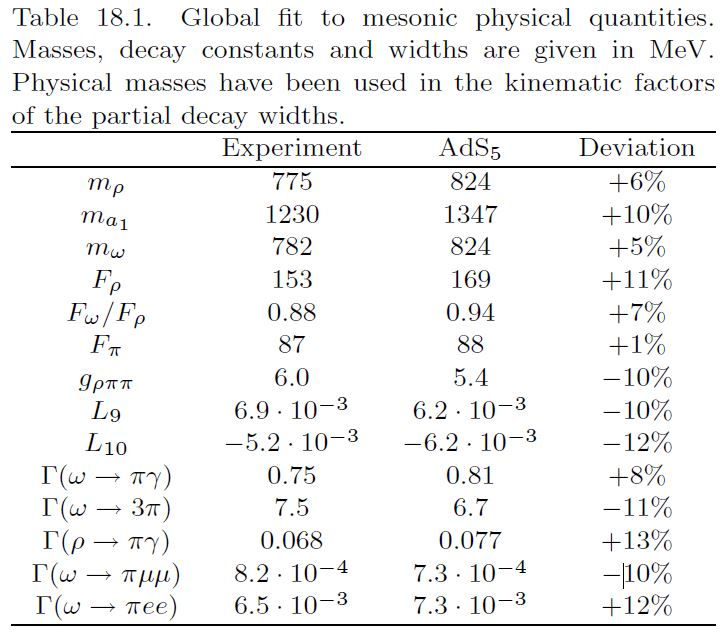
From da Rocha 21, for vector mesons:
for upsilon-mesons:
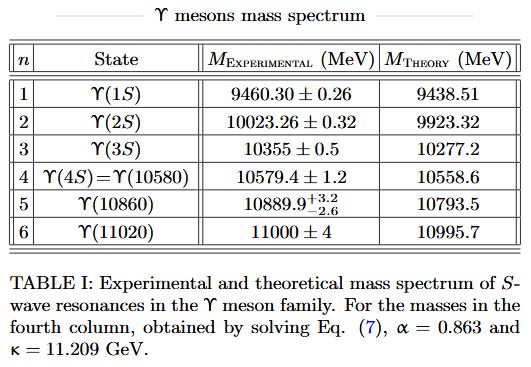
for psi-mesons:
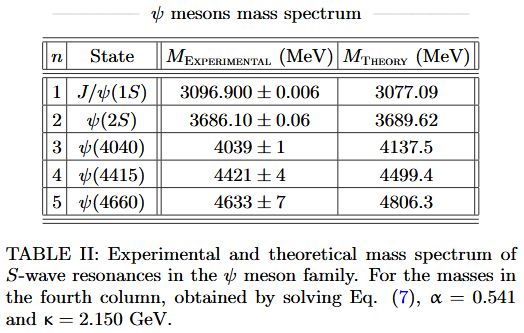
for omega-mesons:
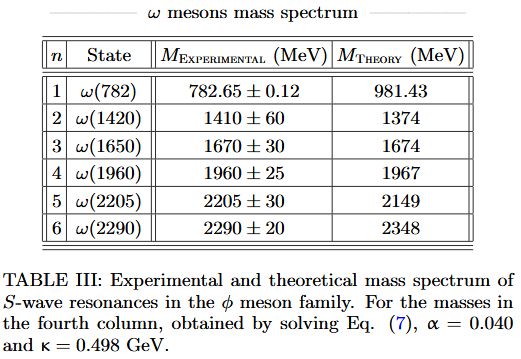
for phi-mesons:

Including the first heavy quarks:
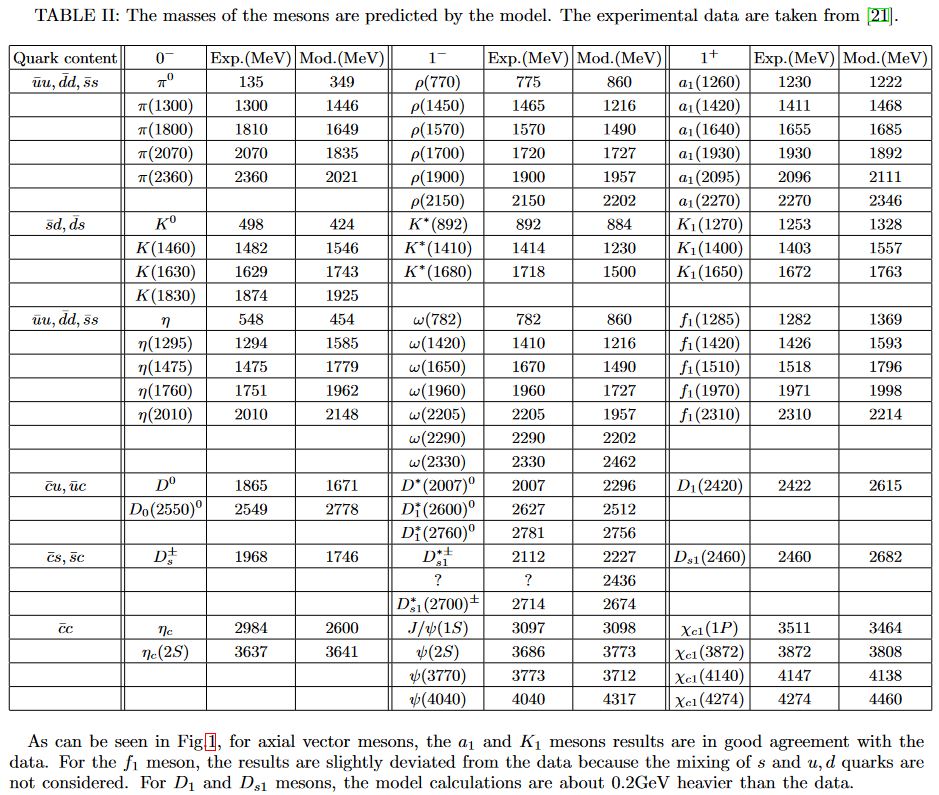
From CLFH22:
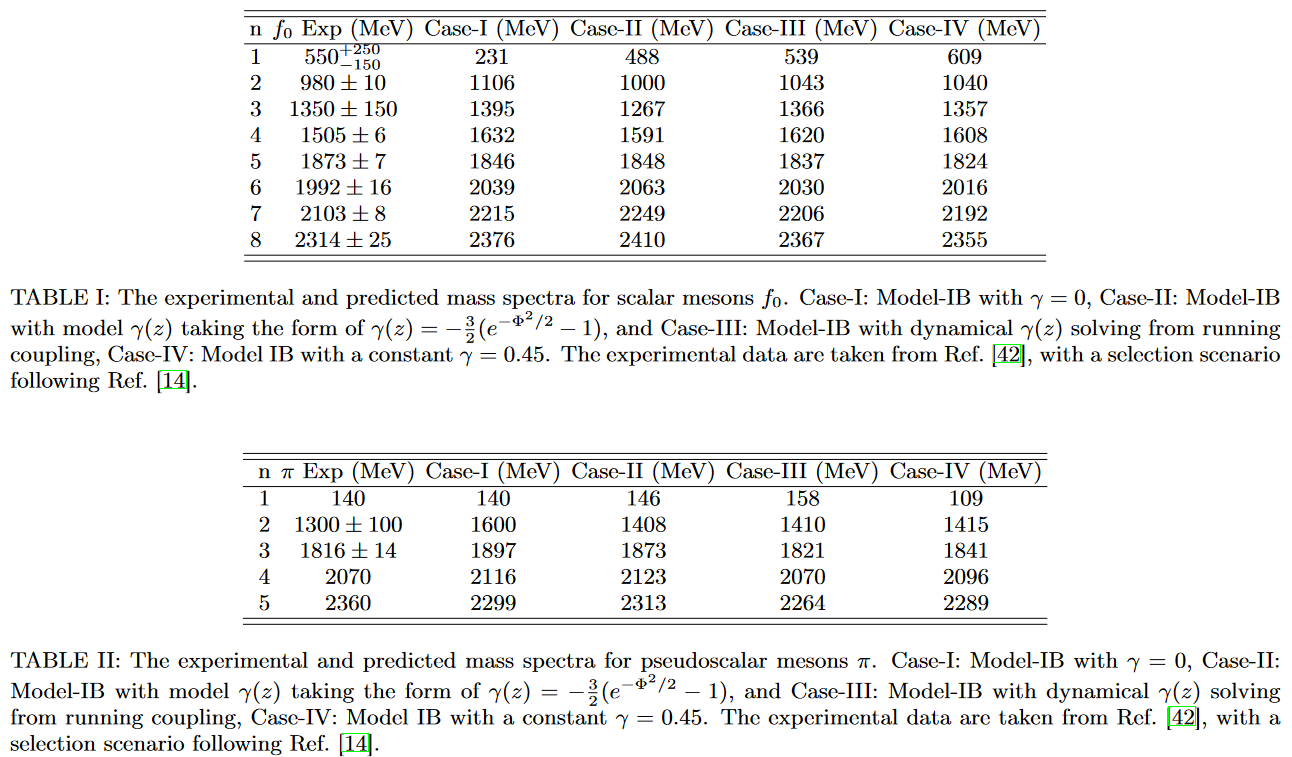
These computations shown so far all use just the field theory in the bulk, not yet the stringy modes (limit of vanishing string length ). Incorporating bulk string corrections further improves these results, see Sonnenschein-Weissman 18.
Embedding into the standard model of particle physics
An obvious question then is can one lift this D brane construction for the holographic dual of QCD to a Standard Model embedding? I study this question in the context of D-brane-world GUT models and find that one needs to have TeV-scale string theory?.
Related concepts
effective field theories of nuclear physics, hence for confined-phase quantum chromodynamics:
References
Polyakov gauge/string duality
Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see notably also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical remarks in Polyakov (2008)) under the name gauge/string duality (cf. historical review in Polyakov (2008)), in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings:
Early suggestion that confined QCD is described by regarding the color-flux tubes as string-like dynamical degrees of freedoms:
-
John Kogut, Leonard Susskind, Vacuum polarization and the absence of free quarks in four dimensions, Phys. Rev. D 9 (1974) 3501-3512 doi:10.1103/PhysRevD.9.3501
-
Kenneth G. Wilson, Confinement of quarks, Phys. Rev. D 10 (1974) 2445 doi:10.1103/PhysRevD.10.2445
(argument in lattice gauge theory)
-
John Kogut, Leonard Susskind, Hamiltonian formulation of Wilson’s lattice gauge theories, Phys. Rev. D 11 (1975) 395 doi:10.1103/PhysRevD.11.395
“The gauge-invariant configuration space consists of a collection of strings with quarks at their ends. The strings are lines of non-Abelian electric flux. In the strong coupling limit the dynamics is best described in terms of these strings. Quark confinement is a result of the inability to break a string without producing a pair. …”
“The confining mechanism is the appearance of one dimensional electric flux tubes which must link separated quarks. The appropriate description of the strongly coupled limit consists of a theory of interacting, propagating strings. …”
“This picture of the strongly coupled Yang-Mills theory in terms of a collection of stringlike flux lines is the central result of our analysis. It should be compared with the phenomenological use of stringlike degrees of freedom which has been widely used in describing hadrons.”
-
Alexander Polyakov, String representations and hidden symmetries for gauge fields, Physics Letters B 82 2 (1979) 247-250 doi:10.1016/0370-2693(79)90747-0
-
Alexander Polyakov, Gauge fields as rings of glue, Nuclear Physics B 164 (1980) 171-188 doi:10.1016/0550-3213(80)90507-6
“The basic idea is that gauge fields can be considered as chiral fields, defined on the space of all possible contours (the loop space). The origin of the idea lies in the expectation that, in the confining phase of a gauge theory, closed strings should play the role of elementary excitations.”
-
Yuri Makeenko, Alexander A. Migdal, Quantum chromodynamics as dynamics of loops, Nuclear Physics B 188 2 (1981) 269-316 doi:10.1016/0550-3213(81)90258-3
“So the world sheet of string should be interpreted as the color magnetic dipole sheet. The string itself should be interpreted as the electric flux tube in the monopole plasma.”
-
Alexander Polyakov, Gauge Fields and Strings, Routledge, Taylor and Francis (1987, 2021) doi:10.1201/9780203755082, oapen:20.500.12657/50871
old personal page: “My main interests this year 1993? were directed towards string theory of quark confinement. The problem is to find the string Lagrangian for the Faraday’s ”lines of force“,which would reproduce perturbative corrections from the Yang-Mills theory to the Coulomb law at small distances and would give permanent confinement of quarks at large distances.”
Cf. also
- Alexei Morozov, p. 6 of: String theory: what is it?, Sov. Phys. Usp. 35 (1992) 671-714 [doi:10.1070/PU1992v035n08ABEH002255]
Early suggestion, due to the Liouville field seen in the quantization of the bosonic string via the Polyakov action,
- Alexander Polyakov, Quantum geometry of bosonic strings, Phys. Lett. B 103 (1981) 207-210 [doi:10.1016/0370-2693(81)90743-7, pdf]
that such flux tubes regarded as confining strings are to be thought of a probing higher dimensional spacetime, exhibiting a holographic principle in which actual spacetime appears as a brane:
-
Alexander Polyakov, String Theory and Quark Confinement, talk at Strings’97, Nucl. Phys. Proc. Suppl. 68 (1998) 1-8 arXiv:hep-th/9711002, doi:10.1016/S0920-5632(98)00135-2
“In other words the open string flies in the -space keeping its feet (its ends) on the ground .”
-
Alexander Polyakov, The wall of the cave, Int. J. Mod. Phys. A 14 (1999) 645-658 arXiv:hep-th/9809057, doi:10.1142/S0217751X99000324
“We add new arguments that the Yang-Mills theories must be described by the non-critical strings in the five dimensional curved space. The physical meaning of the fifth dimension is that of the renormalization scale represented by the Liouville field.”
eventually culminating in the formulation of the dictionary for the AdS-CFT correspondence:
- Steven Gubser, Igor Klebanov, Alexander Polyakov, Gauge theory correlators from non-critical string theory, Physics Letters B 428 105-114 (1998) hep-th/9802109, doi:10.1016/S0370-2693(98)00377-3
“Relations between gauge fields and strings present an old, fascinating and unanswered question. The full answer to this question is of great importance for theoretical physics. It will provide us with a theory of quark confinement by explaining the dynamics of color-electric fluxes.”
- Alexander Polyakov, Vyacheslav Rychkov Gauge fields-strings duality and the loop equation, Nucl. Phys. B 581 (2000) 116-134 arXiv:hep-th/0002106, doi:10.1016/S0550-3213(00)00183-8
and the suggestion of finding the string-QCD correspondence:
- Alexander Polyakov, Gauge Fields and Space-Time, Int. J. Mod. Phys. A 17 S1 (2002) 119-136 arXiv:hep-th/0110196, doi:10.1142/S0217751X02013071
“in the strong coupling limit of a lattice gauge theory the elementary excitations are represented by closed strings formed by the color-electric fluxes. In the presence of quarks these strings open up and end on the quarks, thus guaranteeing quark confinement. Moreover, in the gauge theory the strings interaction is weak at large . This fact makes it reasonable to expect that also in the physically interesting continuous limit (not accessible by the strong coupling approximation) the best description of the theory should involve the flux lines (strings) and not fields, thus returning us from Maxwell to Faraday. In other words it is natural to expect an exact duality between gauge fields and strings. The challenge is to build a precise theory on the string side of this duality.”
Historical reminiscences:
- Alexander Polyakov, Confinement and Liberation, in Gerardus ’t Hooft (ed.) 50 Years of Yang-Mills Theory (2005) 311-329 arXiv:hep-th/0407209, doi:10.1142/9789812567147_0013, doi:10.1142/5601
“Already in 1974, in his famous large paper, ‘t Hooft already tried to find the string-gauge connections. His idea was that the lines of Feynman’s diagrams become dense in a certain sense and could be described as a 2d surface. This is, however, very different from the picture of strings as flux lines. Interestingly, even now people often don’t distinguish between these approaches. In fact, for the usual amplitudes Feynman’s diagrams don’t become dense and the flux lines picture is an appropriate one. However there are cases in which t’Hooft’s mechanism is really working.”
-
Alexander M. Polyakov, §1 in: Beyond Space-Time, in The Quantum Structure of Space and Time, Proceedings of the 23rd Solvay Conference on Physics, World Scientific (2007) arXiv:hep-th/0602011, pdf
-
Alexander M. Polyakov, From Quarks to Strings arXiv:0812.0183
published as Quarks, strings and beyond, section 44 in: Paolo Di Vecchia et al. (ed.), The Birth of String Theory, Cambridge University Press (2012) 544-551 doi:10.1017/CBO9780511977725.048
“By the end of ’77 it was clear to me that I needed a new strategy for understanding confinement and I became convinced that the way to go was the gauge/string duality. …”
“Classically the string is infinitely thin and has only transverse oscillations. But when I quantized it there was a surprise – an extra, longitudinal mode, which appears due to the quantum ”thickening“ of the string. This new field is called the Liouville mode. …”
“I kept thinking about gauge/strings dualities. Soon after the Liouville mode was discovered it became clear to many people including myself that its natural interpretation is that random surfaces in 4d are described by the strings flying in 5d with the Liouville field playing the role of the fifth dimension. The precise meaning of this statement is that the wave function of the general string state depends on the four center of mass coordinates and also on the fifth, the Liouville one. In the case of minimal models this extra dimension is related to the matrix eigenvalues and the resulting space is flat.”
“Since this 5d space must contain the flat 4d subspace in which the gauge theory resides, the natural ansatz for the metric is just the Friedman universe with a certain warp factor. This factor must be determined from the conditions of conformal symmetry on the world sheet. Its dependence on the Liouville mode must be related to the renormalization group flow. As a result we arrive at a fascinating picture – our 4d world is a projection of a more fundamental 5d string theory. …”
“At this point I was certain that I have found the right language for the gauge/string duality. I attended various conferences, telling people that it is possible to describe gauge theories by solving Einstein-like equations (coming from the conformal symmetry on the world sheet) in five dimensions. The impact of my talks was close to zero. That was not unusual and didn’t bother me much. What really caused me to delay the publication (Polyakov 1998) for a couple of years was my inability to derive the asymptotic freedom from my equations. At this point I should have noticed the paper of Klebanov 1997 in which he related D3 branes described by the supersymmetric Yang Mills theory to the same object described by supergravity. Unfortunately I wrongly thought that the paper is related to matrix theory and I was skeptical about this subject. As a result I have missed this paper which would provide me with a nice special case of my program. This special case was presented little later in full generality by Juan Maldacena (Maldacena 1997) and his work opened the flood gates.”
A detailed monograph:
-
N. D. Hari Dass, Strings to Strings – Yang-Mills Flux Tubes, QCD Strings and Effective String Theories, Lecture Notes in Physics 1018, Springer (2024) [doi:10.1007/978-3-031-35358-1]
Ch. 23:
Effective String Theories (EST) of Yang-Mills Flux Tubes [doi:10.1007/978-3-031-35358-1_22, arXiv:2312.10629]
General
Review and introduction
-
Ofer Aharony, The non-AdS/non-CFT correspondence, or three different paths to QCD, Progress in string, field and particle theory. Springer, Dordrecht, 2003. 3-24 (arXiv:hep-th/0212193)
-
Joshua Erlich, How Well Does AdS/QCD Describe QCD?, Int. J. Mod. Phys.A 25 (2010) 411-421 [arXiv:0908.0312, doi:10.1142/S0217751X10048718]
-
Marco Panero, QCD thermodynamics in the large- limit, 2010 (PaneroAdsQCD.pdf)
-
Youngman Kim, Deokhyun Yi, Holography at Work for Nuclear and Hadron Physics, Advances in High Energy Physics, Volume 2011, Article ID 259025, 62 pages (arXiv:1107.0155, doi:10.1155/2011/259025)
-
Antoine Van Proeyen, Daniel Freedman, Chapter VIII of: Supergravity, Cambridge University Press (2012) [doi:10.1017/CBO9781139026833]
-
Koji Hashimoto, §6.4 in: D-Brane – Superstrings and New Perspective of Our World, Springer (2012) [doi:10.1007/978-3-642-23574-0, spire:1188897]
-
M. R. Pahlavani, R. Morad, Application of AdS/CFT in Nuclear Physics, Advances in High Energy Physics (arXiv:1403.2501)
-
Jorge Casalderrey-Solana, Hong Liu, David Mateos, Krishna Rajagopal, Urs Achim Wiedemann, Gauge/string duality, hot QCD and heavy ion collisions, Cambridge University Press, 2014 (arXiv:1101.0618)
-
Sinya Aoki, Koji Hashimoto, Norihiro Iizuka, Matrix Theory for Baryons: An Overview of Holographic QCD for Nuclear Physics, Reports on Progress in Physics, Volume 76, Number 10 (arxiv:1203.5386)
-
Youngman Kim, Ik Jae Shin, Takuya Tsukioka, Holographic QCD: Past, Present, and Future, Progress in Particle and Nuclear Physics 68 (2013) 55-112 [arXiv:1205.4852]
-
Joshua Erlich, An Introduction to Holographic QCD for Nonspecialists, Contemporary Physics, 56 2 (2015) [arXiv:1407.5002, doi:10.1080/00107514.2014.942079]
-
Alberto Guijosa, QCD, with Strings Attached, IJMPE Vol. 25, No. 10 (2016) 1630006 (arXiv:1611.07472)
-
Mannque Rho, Ismail Zahed (eds.) Chapter 4 of: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Sophia K Domokos, Robert Bell, Trinh La, Patrick Mazza, A Pedagogical Introduction to Holographic Hadrons, published as: Holographic hadron masses in the language of quantum mechanics, European Journal of Physics 42 6 (2021) 065801 [arXiv:2106.13136, doi:10.1088/1361-6404/ac1abb]
With emphasis on application to the QCD phase diagram and to the description of neutron stars:
-
Matti Järvinen, Holographic modeling of nuclear matter and neutron stars, Eur.Phys.J.C. 56 2021 (arXiv:2110.08281)
-
Niko Jokela, NICER view on holographic QCD (arXiv:2111.07940)
See also:
- Wikipedia, AdS/QCD correspondence
Emphasis of the AdS-QCD correspondence at annual String-conferences:
-
Igor Klebanov, Remarks on Color Confinement, talk at Strings 2021 (pdf, video)
-
Sergei Dubovsky, Comments on (mostly long) QCD strings, talk at Strings 2021 (pdf, video)
-
Nick Evans, Holography for Multi-Representation and Chiral Matter, talk at Strings 2022 [indico:4940848, slides, video]
(emphasis on DBI action-effects)
-
Umut Gürsoy, Recent developments in gauge-gravity duality applied to quantum many-body systems, talk at Strings 2022 [indico:4940863, pdf, video ]
-
Edward Witten, Some Milestones in the Study of Confinement, talk at Prospects in Theoretical Physics 2023 – Understanding Confinement, IAS (2023) [web, YT]
40:13: “Personally, I think this setup really implies that pure gauge theory is dual to a string theory. The ‘only’ problem is that to get the pure gauge theory we need to make a relevant deformation and then take the limit that the deformation parameter is large…”
Top-down models
Witten-Sakai-Sugimoto model
Precursor developments:
-
Tohru Eguchi, Hikaru Kawai, Reduction of Dynamical Degrees of Freedom in the Large- Gauge Theory, Phys. Rev. Lett. 48, 1063 (1982) (spire:176459, doi:10.1103/PhysRevLett.48.1063)
-
Joseph Polchinski, Matthew Strassler, The String Dual of a Confining Four-Dimensional Gauge Theory (arXiv:hep-th/0003136)
(discussion of confinement via AdS/CFT with a Myers effect in the bulk)
The top-down Sakai-Sugimoto model is due to
-
Tadakatsu Sakai, Shigeki Sugimoto, Low energy hadron physics in holographic QCD, Progr. Theor. Phys. 113: 843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, More on a holographic dual of QCD, Progr. Theor. Phys. 114: 1083-1118, 2005 (arXiv:hep-th/0507073)
along the lines of
- Andreas Karch, Emanuel Katz, Adding flavor to AdS/CFT, JHEP 0206:043, 2002 (arxiv:hep-th/0205236)
and based on
- Edward Witten, Anti-de Sitter Space, Thermal Phase Transition, And Confinement In Gauge Theories, Adv. Theor. Math. Phys.2:505-532, 1998 (arXiv:hep-th/9803131)
further developed in
- Lorenzo Bartolini, Stefano Bolognesi, Andrea Proto, From the Sakai-Sugimoto Model to the Generalized Skyrme Model, Phys. Rev. D 97, 014024 2018 (arXiv:1711.03873)
reviewed in:
-
Piljin Yi, Topics in D4-D8 holographic QCD, 2009 (pdf slides)
-
Shigeki Sugimoto, Holographic QCD – Status and perspectives, 2012 (pdf slides)
-
Anton Rebhan, The Witten-Sakai-Sugimoto model: A brief review and some recent results, 3rd International Conference on New Frontiers in Physics, Kolymbari, Crete, 2014 (arXiv:1410.8858)
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Si-wen Li, Xiao-tong Zhang, The D4/D8 model and holographic QCD [arXiv:2304.10826]
See also:
- Vikas Yadav, String/-theory Dual of Large- Thermal QCD-Like Theories at Intermediate Gauge/‘t Hooft Coupling and Holographic Phenomenology (arXiv:2111.12655)
More on D4-D8 brane bound states:
- Horatiu Nastase, Sections 2, 3 of: On Dp-Dp+4 systems, QCD dual and phenomenology (arXiv:hep-th/0305069)
The Witten-Sakai-Sugimoto model with orthogonal gauge groups realized by D4-D8 brane bound states at O-planes:
-
Toshiya Imoto, Tadakatsu Sakai, Shigeki Sugimoto, and QCD from String Theory, Prog.Theor.Phys.122:1433-1453, 2010 (arXiv:0907.2968)
-
Hee-Cheol Kim, Sung-Soo Kim, Kimyeong Lee, 5-dim Superconformal Index with Enhanced Global Symmetry, JHEP 1210 (2012) 142 (arXiv:1206.6781)
Analogous discussion for flavour D6-branes:
-
Jérôme Gaillard, On -structures in gauge/string duality, 2011 (cronfa:42569 spire:1340775, pdf)
(with emphasis of G-structures)
The analogoue of the WSS model for 2d QCD:
- Yi-hong Gao, Weishui Xu, Ding-fang Zeng, NGN, and chiral phase transition from string theory, Nucl.Phys. B400:181-210, 1993 (arXiv:hep-th/0605138)
Specifically concerning the 3d Chern-Simons theory on the D8-branes:
- Ho-Ung Yee, Ismail Zahed, Holographic two dimensional QCD and Chern-Simons term, JHEP 1107:033, 2011 (arXiv:1103.6286)
and its relation to baryons:
- Hideo Suganuma, Yuya Nakagawa, Kohei Matsumoto, 1+1 Large QCD and its Holographic Dual Soliton Picture of Baryons in Single-Flavor World, JPS Conf. Proc. 13, 020013 (2017) (arXiv:1610.02074)
On jet bundle cohomology in the Sakai-Sugimoto model:
- Ekkehart Winterroth, Variational cohomology and Chern-Simons gauge theories in higher dimensions (arXiv:2103.03037)
Further models
Variant with D4 flavor branes:
-
Mark Van Raamsdonk, Kevin Whyte, Baryon charge from embedding topology and a continuous meson spectrum in a new holographic gauge theory, JHEP 1005:073, 2010 (arXiv:0912.0752)
-
Shigenori Seki, Intersecting D4-branes Model of Holographic QCD and Tachyon Condensation, JHEP 1007:091, 2010 (arXiv:1003.2971)
See also:
-
Nick Evans, Jack Mitchell, Domain Wall AdS/QCD, Phys. Rev. D 104 (2021) 094018 [arXiv:2108.12152, doi:10.1103/PhysRevD.104.094018]
-
Nick Evans, Jack Mitchell, Thermal Transitions in Domain Wall AdS/QCD [arXiv:2207.10374]
Bottom-up models
Hard- and soft-wall model
The bottom-up hard-wall model is due to
- Joshua Erlich, Emanuel Katz, Dam T. Son, Mikhail A. Stephanov, QCD and a Holographic Model of Hadrons, Phys.Rev.Lett.95:261602, 2005 (arXiv:hep-ph/0501128)
while the soft-wall refinement is due to
- Andreas Karch, Emanuel Katz, Dam T. Son, Mikhail A. Stephanov, Linear Confinement and AdS/QCD, Phys.Rev.D74:015005, 2006 (arXiv:hep-ph/0602229)
reviewed in
- Sergey Afonin, Timofey Solomko, Motivations for the Soft Wall holographic approach to strong interactions [arXiv:2209.09042]
see also
-
Alfredo Vega, Paulina Cabrera, Family of dilatons and metrics for AdS/QCD models, Phys. Rev. D 93, 114026 (2016) (arXiv:1601.05999)
-
Alfonso Ballon-Bayona, Luis A. H. Mamani, Nonlinear realisation of chiral symmetry breaking in holographic soft wall models (arXiv:2002.00075)
and the version improved holographic QCD is due to
-
Umut Gursoy, Elias Kiritsis, Exploring improved holographic theories for QCD: Part I, JHEP 0802:032, 2008 (arXiv:0707.1324)
-
Umut Gursoy, Elias Kiritsis, Francesco Nitti, Exploring improved holographic theories for QCD: Part II, JHEP 0802:019, 2008 (arXiv:0707.1349)
reviewed in
- Umut Gürsoy, Elias Kiritsis, Liuba Mazzanti, Georgios Michalogiorgakis, Francesco Nitti, Improved Holographic QCD, Lect.Notes Phys.828:79-146,2011 (arXiv:1006.5461)
More developments on improved holographic QCD:
- Takaaki Ishii, Matti Järvinen, Govert Nijs, Cool baryon and quark matter in holographic QCD (arXiv:1903.06169)
The extreme form of bottom-up holographic model building is explored in
- Koji Hashimoto, Sotaro Sugishita, Akinori Tanaka, Akio Tomiya, Deep Learning and Holographic QCD, Phys. Rev. D 98, 106014 (2018) (arXiv:1809.10536)
where an appropriate bulk geometry is computer-generated from specified boundary behaviour.
- Tetsuya Akutagawa, Koji Hashimoto, Takayuki Sumimoto, Deep Learning and AdS/QCD (arXiv:2005.02636)
On the other hand, an embedding of the hard-wall model into type IIB string theory is discussed in:
-
Akash Singh, K. P. Yogendran, Phases of a 10-D Holographic hard wall model [arXiv:2208.09387]
-
Saulo Diles, On the spectrum of open strings in the Hard-Wall model of AdS/QCD: the role of [arXiv:2404.10183]
Holographic light-front QCD
The holographic formulation of light cone quantized QCD as holographic light front QCD:
Original articles:
-
Stanley Brodsky, Guy de Teramond, Light-Front Hadron Dynamics and AdS/CFT Correspondence, Phys. Lett. B582:211-221, 2004 (arXiv:hep-th/0310227)
-
Guy de Teramond, Stanley Brodsky, Light-Front Holography: A First Approximation to QCD, Phys. Rev. Lett. 102:081601, 2009 (arXiv:0809.4899)
Review in:
-
Stanley Brodsky, Guy de Teramond, Hans Günter Dosch, Joshua Erlich,
Light-Front Holographic QCD and Emerging Confinement, Physics Reports Volume 584, 8 July 2015, Pages 1-105 (arXiv:1407.8131)
-
Liping Zou, Hans Günter Dosch, A very Practical Guide to Light Front Holographic QCD, (arXiv:1801.00607)
-
Stanley Brodsky, Color Confinement and Supersymmetric Properties of Hadron Physics from Light-Front Holography, International Conference on Beauty, Charm and Hyperon Hadrons (BEACH 2018) 17–23 June 2018, Peniche, Portugal (arXiv:1912.12578)
-
Ruben Sandapen, An overview of light-front holography (arXiv:2001.03479)
-
Stanley Brodsky, Supersymmetric and Other Novel Features of Hadron Physics from Light-Front Holography, Proceedings of the 24th Workshop, “What Comes Beyond the Standard Models” (arXiv:2112.02453)
See also
- Harun Omer, Embedding LFHQCD in Worldsheet String Theory (arXiv:1909.12866)
Application to B-meson physics:
- Mohammad Ahmady, Holographic light-front QCD in B meson phenomenology (arXiv:2001.00266)
Relation to hadron supersymmetry
Discussion of hadron supersymmetry via light cone supersymmetric quantum mechanics in holographic light front QCD:
-
Guy de Teramond, Hans Günter Dosch, Stanley Brodsky, Baryon Spectrum from Superconformal Quantum Mechanics and its Light-Front Holographic Embedding, Phys. Rev. D 91, 045040 (2015) (arXiv:1411.5243)
-
Hans Günter Dosch, Guy de Teramond, Stanley Brodsky, Supersymmetry Across the Light and Heavy-Light Hadronic Spectrum, Phys. Rev. D 92, 074010 (2015) (arXiv:1504.05112)
-
Stanley Brodsky, Guy de Téramond, Hans Günter Dosch, Cédric Lorcé, Meson/Baryon/Tetraquark Supersymmetry from Superconformal Algebra and Light-Front Holography, International Journal of Modern Physics AVol. 31, No. 19, 1630029 (2016) (arXiv:1606.04638)
-
Hans Günter Dosch, Guy de Teramond, Stanley Brodsky, Supersymmetry Across the Light and Heavy-Light Hadronic Spectrum II, Phys. Rev. D 95, 034016 (2017) (arXiv:1612.02370)
-
Marina Nielsen, Stanley Brodsky, Hadronic Superpartners from Superconformal and Supersymmetric Algebra, Phys. Rev. D 97, 114001 (2018) (arXiv:1802.09652)
-
Marina Nielsen, Stanley Brodsky, Guy F. de Téramond, Hans Günter Dosch, Fernando S. Navarra, Liping Zou, Supersymmetry in the Double-Heavy Hadronic Spectrum, Phys. Rev. D 98, 034002 (2018) (arXiv:1805.11567)
String- and M-theory corrections
Generally on perturbative string theory-corrections (for small 't Hooft coupling ) and/or M-theory-corrections (small N) to the supergravity-approximation of the AdS/CFT correspondence, i.e. the small N corrections to the correspondence:
On the general need for M-theory at small in gauge/gravity duality:
-
Leonard Susskind, Another Conjecture about M(atrix) Theory (arXiv:hep-th/9704080)
-
Nissan Itzhaki, Juan Maldacena, Jacob Sonnenschein, Shimon Yankielowicz, Section 6 of: Supergravity and The Large Limit of Theories With Sixteen Supercharges, Phys. Rev. D 58, 046004 (1998) (arXiv:hep-th/9802042)
Discussion of small N effects in M-theory AdS4/CFT3 and using the conformal bootstrap:
- Nathan B. Agmon, Shai M. Chester, Silviu S. Pufu, Solving M-theory with the Conformal Bootstrap, JHEP 06 (2018) 159 (arXiv:1711.07343)
Specifically on small N corrections in holographic QCD:
-
B. Basso, Cusp anomalous dimension in planar maximally supersymmetric Yang-Mills theory, Continuous Advances in QCD 2008, pp. 317-328 (2008) (spire:858223, doi:10.1142/9789812838667_0027)
“The result (29) coincides exactly with the recent two-loop stringy correction computed in Alday-Maldacena 07, providing a striking confirmation of the AdS/CFT correspondence.”
-
H. Dorn, H.-J. Otto, On Wilson loops and -potentials from the AdS/CFT relation at , In: Anna Ceresole, C. Kounnas , Dieter Lüst, Stefan Theisen (eds.) Quantum Aspects of Gauge Theories, Supersymmetry and Unification, Lecture Notes in Physics, vol 525. Springer 2007 (arXiv:hep-th/9812109, doi:10.1007/BFb0104268)
-
Masayasu Harada, Shinya Matsuzaki, and Koichi Yamawaki, Implications of holographic QCD in chiral perturbation theory with hidden local symmetry, Phys. Rev. D 74, 076004 (2006) (doi:10.1103/PhysRevD.74.076004)
(with an eye towards hidden local symmetry)
-
Csaba Csaki, Matthew Reece, John Terning, The AdS/QCD Correspondence: Still Undelivered, JHEP 0905:067, 2009 (arXiv:0811.3001)
-
Salvatore Baldino, Stefano Bolognesi, Sven Bjarke Gudnason, Deniz Koksal, A Solitonic Approach to Holographic Nuclear Physics, Phys. Rev. D 96, 034008 (2017) (arXiv:1703.08695)
-
Vikas Yadav, Aalok Misra, On M-Theory Dual of Large- Thermal QCD-Like Theories up to and -Structure Classification of Underlying Non-Supersymmetric Geometries (arXiv:2004.07259)
Hadrons as KK-modes of 5d Yang-Mills theory
The suggestion that the tower of observed vector mesons – when regarded as gauge fields of hidden local symmetries of chiral perturbation theory – is reasonably modeled as a Kaluza-Klein tower of D=5 Yang-Mills theory:
- D. T. Son, M. A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182, doi:10.1103/PhysRevD.69.065020)
That the pure pion-Skyrmion-model of baryons is approximately the KK-reduction of instantons in D=5 Yang-Mills theory is already due to:
- Michael Atiyah, Nicholas Manton, Skyrmions from instantons, Phys. Lett. B, 222(3):438–442, 1989 (doi:10.1016/0370-2693(89)90340-7)
with a hyperbolic space-variant in:
- Michael Atiyah, Paul Sutcliffe, Skyrmions, instantons, mass and curvature, Phys. Lett. B605 (2005) 106-114 (arXiv:hep-th/0411052)
Further discussion of this approximation:
- Josh Cork, Chris Halcrow, ADHM skyrmions (arXiv:2110.15190)
The observation that the result of Atiyah-Manton 89 becomes an exact Kaluza-Klein construction of Skyrmions/baryons from D=5 instantons when the full KK-tower of vector mesons as in Son-Stephanov 03 is included into the Skyrmion model (see also there) is due to:
-
Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
-
Paul Sutcliffe, Holographic Skyrmions, Mod. Phys. Lett. B29 (2015) no. 16, 1540051 (spire:1383608, doi:10.1142/S0217984915400515)
In the Sakai-Sugimoto model of holographic QCD the D=5 Yang-Mills theory of this hadron Kaluza-Klein theory is identified with the worldvolume-theory of D8-flavour branes intersected with D4-branes in an intersecting D-brane model:
-
Tadakatsu Sakai, Shigeki Sugimoto, section 5.2 of Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, section 3.3. of More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)
-
Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, Shinichiro Yamato, Baryons from instantons in holographic QCD, Prog.Theor.Phys.117:1157, 2007 (arXiv:hep-th/0701280)
-
Stefano Bolognesi, Paul Sutcliffe, The Sakai-Sugimoto soliton, JHEP 1401:078, 2014 (arXiv:1309.1396)
-
Lorenzo Bartolini, Stefano Bolognesi, Andrea Proto, From the Sakai-Sugimoto Model to the Generalized Skyrme Model, Phys. Rev. D 97 014024 (2018) [doi:10.1103/PhysRevD.97.014024, arXiv:1711.03873]
-
Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Tommaso Rainaldi, Mass and Isospin Breaking Effects in the Skyrme Model and in Holographic QCD [arXiv:2312.15404]
Extensive review of this holographic/KK-theoretic-realization of quantum hadrodynamics from D=5 Yang-Mills theory is in:
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific, Second edition, 2016 (doi:10.1142/9710)
- Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Via the realization of D4/D8 brane bound states as instantons in the D8-brane worldvolume-theory (see there and there), this relates also to the model of baryons as wrapped D4-branes, originally due to
-
Edward Witten, Baryons And Branes In Anti de Sitter Space, JHEP 9807:006, 1998 (arXiv:hep-th/9805112)
-
David Gross, Hirosi Ooguri, Aspects of Large Gauge Theory Dynamics as Seen by String Theory, Phys. Rev. D58:106002, 1998 (arXiv:hep-th/9805129)
and further developed in the nuclear matrix model:
-
Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
In relation to Yang-Mills monopoles:
- Stefano Bolognesi, Solitons, Large and Holography, 2015 (pdf)
Discussion, in this context, of D-term effects affecting hadron stability:
- Mitsutoshi Fujita, Yoshitaka Hatta, Shigeki Sugimoto, Takahiro Ueda, Nucleon D-term in holographic QCD arXiv:2206.06578
More on baryons in the Sakai-Sugimoto model of holographic QCD:
- Salvatore Baldino, Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Holographic Nuclear Physics with Massive Quarks, Phys. Rev. D 103 126015 (2021) [doi:10.1103/PhysRevD.103.126015, arXiv:2102.00680]
More on mesons in holographic QCD:
-
Johanna Erdmenger, Nick Evans, Ingo Kirsch, Ed Threlfall, Mesons in Gauge/Gravity Duals - A Review, Eur. Phys. J. A 35 (2008) 81-133 [arXiv:0711.4467, doi:10.1140/epja/i2007-10540-1]
-
Daniel Ávila, Leonardo Patiño, Melting holographic mesons by cooling a magnetized quark gluon plasma (arXiv:2002.02470)
-
Xuanmin Cao, Hui Liu, Danning Li, Pion quasiparticles and QCD phase transitions at finite temperature and isospin density from holography, Phys. Rev. D 102, 126014 (2020) (arXiv:2009.00289)
-
Xuanmin Cao, Songyu Qiu, Hui Liu, Danning Li, Thermal properties of light mesons from holography (arXiv:2102.10946)
-
Artur Amorim, Miguel S. Costa, Matti Järvinen, Regge theory in a Holographic dual of QCD in the Veneziano Limit (arXiv:2102.11296)
-
Roldão da Rocha, Information in AdS/QCD: mass spectroscopy of isovector mesons, Phys. Rev. D 103 106027 (2021) [arXiv:2103.03924, doi:10.1103/PhysRevD.103.106027]
-
Shahin Mamedov, Narmin Nasibova, Temperature dependence of meson-nucleon coupling constant from the soft-wall model (arXiv:2103.10494)
An alternative scenario of derivation of 4d Skyrmions by KK-compactification of D=5 Yang-Mills theory, now on a closed interval, motivated by M5-branes instead of by D4/D8-brane intersections as in the Sakai-Sugimoto model, is discussed in:
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Skyrme model from 6d theory, Physics Letters B Volume 783, 10 August 2018, Pages 222-226 (arXiv:1805.07241)
following
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Non-Abelian sigma models from Yang-Mills theory compactified on a circle, Physics Letters B Volume 781, 10 June 2018, Pages 322-326 (arXiv:1803.07322)
See also:
- Y. H. Ahn, Sin Kyu Kang, Hyun Min Lee, Towards a Model of Quarks and Leptons (arXiv:2112.13392)
Hadron physics
Application to confined hadron-physics:
Review:
-
Henrique Boschi-Filho, Hadrons in AdS/QCD models, Journal of Physics: Conference Series, Volume 706, Section 4 2008 (doi:10.1088/1742-6596/706/4/042008)
-
Kanabu Nawa, Hideo Suganuma, Toru Kojo, Baryons in Holographic QCD, Phys.Rev.D75:086003, 2007 (arXiv:hep-th/0612187)
-
Deog Ki Hong, Mannque Rho, Ho-Ung Yee, Piljin Yi, Chiral Dynamics of Baryons from String Theory, Phys. Rev. D76:061901, 2007 (arXiv:hep-th/0701276)
-
Deog Ki Hong, Baryons in holographic QCD, talk at From Strings to Things 2008 (pdf)
-
Johanna Erdmenger, Nick Evans, Ingo Kirsch, Ed Threlfall, Mesons in Gauge/Gravity Duals - A Review, Eur. Phys. J. A 35 (2008) 81-133 [arXiv:0711.4467, doi:10.1140/epja/i2007-10540-1]
-
Stanley Brodsky, Hadron Spectroscopy and Dynamics from Light-Front Holography and Superconformal Algebra (arXiv:1802.08552)
-
Koji Hashimoto, Tadakatsu Sakai, Shigeki Sugimoto, Holographic Baryons : Static Properties and Form Factors from Gauge/String Duality, Prog. Theor. Phys.120:1093-1137, 2008 (arXiv:0806.3122)
-
Alex Pomarol, Andrea Wulzer, Baryon Physics in Holographic QCD, Nucl. Phys. B809:347-361, 2009 (arXiv:0807.0316)
-
Thomas Gutsche, Valery E. Lyubovitskij, Ivan Schmidt, Alfredo Vega, Nuclear physics in soft-wall AdS/QCD: Deuteron electromagnetic form factors, Phys. Rev. D 91, 114001 (2015) (arXiv:1501.02738)
-
Alex Pomarol, Andrea Wulzer, Baryon physics in a five-dimensional model of hadrons (arXiv:0904.2272), Chapter 18 in: Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Marco Claudio Traini, Generalized Parton Distributions: confining potential effects within AdS/QCD, Eur. Phys. J. C (2017) 77:246 (arXiv:1608.08410)
-
Wenhe Cai, Si-wen Li, Holographic three flavor baryon in the Witten-Sakai-Sugimoto model with the D0-D4 background, Eur. Phys. J. C (2018) 78: 446 (arXiv:1712.06304)
-
Valery E. Lyubovitskij, Ivan Schmidt, Gluon parton densities in soft-wall AdS/QCD (arXiv:2012.01334)
-
Lorenzo Bartolini, Sven Bjarke Gudnason, Symmetry energy in holographic QCD [arXiv:2209.14309]
See also:
- Ruixiang Chen, Danning Li, Kazem Bitaghsir Fadafan, Mei Huang, The hadron spectra and pion form factor in dynamical holographic QCD model with anomalous 5D mass of scalar field [arXiv:2212.10363]
Baryons as instantons
baryons as instantons:
-
Emanuel Katz, Adam Lewandowski, Matthew D. Schwartz, Phys. Rev. D74:086004, 2006 (arXiv:hep-ph/0510388)
-
Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, Shinichiro Yamato, Baryons from instantons in holographic QCD, Prog.Theor.Phys.117:1157, 2007 (arXiv:hep-th/0701280)
-
Hiroyuki Hata, Masaki Murata, Baryons and the Chern-Simons term in holographic QCD with three flavors (arXiv:0710.2579)
-
Salvatore Baldino, Stefano Bolognesi, Sven Bjarke Gudnason, Deniz Koksal, A Solitonic Approach to Holographic Nuclear Physics, Phys. Rev. D 96, 034008 (2017) (arXiv:1703.08695)
-
Chandan Mondal, Dipankar Chakrabarti, Xingbo Zhao, Deuteron transverse densities in holographic QCD, Eur. Phys. J. A 53, 106 (2017) (arXiv:1705.05808)
-
Stanley J. Brodsky, Color Confinement, Hadron Dynamics, and Hadron Spectroscopy from Light-Front Holography and Superconformal Algebra (arXiv:1709.01191)
-
Alfredo Vega, M. A. Martin Contreras, Melting of scalar hadrons in an AdS/QCD model modified by a thermal dilaton (arXiv:1808.09096)
-
Meng Lv, Danning Li, Song He, Pion condensation in a soft-wall AdS/QCD model (arXiv:1811.03828)
-
Kazem Bitaghsir Fadafan, Farideh Kazemian, Andreas Schmitt, Towards a holographic quark-hadron continuity (arXiv:1811.08698)
-
Jacob Sonnenschein, Dorin Weissman, Excited mesons, baryons, glueballs and tetraquarks: Predictions of the Holography Inspired Stringy Hadron model, (arXiv:1812.01619)
-
Kazem Bitaghsir Fadafan, Farideh Kazemian, Andreas Schmitt, Towards a holographic quark-hadron continuity (arXiv:1811.08698)
-
M. Abdolmaleki, G.R. Boroun, The Survey of Proton Structure Function with the AdS/QCD Correspondence Phys.Part.Nucl.Lett. 15 (2018) no.6, 581-584 (doi:10.1134/S154747711806002X)
-
Si-wen Li, Hao-qian Li, Sen-kai Luo, Corrections to the instanton configuration as baryon in holographic QCD [arXiv:2209.12521]
On relation to type 0 string theory:
-
Roberto Grena, Simone Lelli, Michele Maggiore, Anna Rissone, Confinement, asymptotic freedom and renormalons in type 0 string duals, JHEP 0007 (2000) 005 (arXiv:hep-th/0005213)
-
Mohammad Akhond, Adi Armoni, Stefano Speziali, Phases of from Type 0 Strings and Seiberg Duality (arxiv:1908.04324)
See also
- S. S. Afonin, AdS/QCD without Kaluza-Klein modes: Radial spectrum from higher dimensional QCD operators (arXiv:1905.13086)
In relation to the open string tachyon:
- M. Järvinen, E. Kiritsis, F. Nitti, E. Préau, Tachyon-dependent Chern-Simons terms and the V-QCD Baryon [arXiv:2209.05868]
See also:
- Keiichiro Hori, Hideo Suganuma, Hiroki Kanda, Numerical analysis of a baryon and its dilatation modes in holographic QCD [arXiv:2307.16590]
Baryons as wrapped branes
original articles:
-
Edward Witten, Baryons And Branes In Anti de Sitter Space, JHEP 9807:006, 1998 (arXiv:hep-th/9805112)
-
David Gross, Hirosi Ooguri, Aspects of Large Gauge Theory Dynamics as Seen by String Theory, Phys. Rev. D58:106002, 1998 (arXiv:hep-th/9805129)
-
A. Brandhuber, N. Itzhaki, Jacob Sonnenschein, Shimon Yankielowicz, Baryons from Supergravity, JHEP 9807:020, 1998 (arxiv:hep-th/9806158)
-
Yosuke Imamura, Supersymmetries and BPS Configurations on Anti-de Sitter Space, Nucl. Phys. B537:184-202, 1999 (arxiv:hep-th/9807179)
-
Curtis Callan, Alberto Guijosa, Konstantin G. Savvidy, Baryons and String Creation from the Fivebrane Worldvolume Action (arxiv:hep-th/9810092)
-
Curtis Callan, Alberto Guijosa, Konstantin G. Savvidy, Oyvind Tafjord, Baryons and Flux Tubes in Confining Gauge Theories from Brane Actions, Nucl. Phys. B555 (1999) 183-200 (arxiv:hep-th/9902197)
Review:
-
Piljin Yi, Holographic Baryons (arXiv:0902.4515, doi:10.1142/9789814280709_0016), Chapter 16 in: Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Piljin Yi, Precision Holographic Baryons, AIP Conference Proceedings 1388, 106 (2011) (arXiv:1103.1684, doi:10.1063/1.3647358)
-
Piljin Yi, Two Approaches to Holographic Baryons/Nuclei, Few-Body Syst (2013) 54: 77. (doi:10.1007/s00601-012-0373-7)
Baryons as Skyrmions
Review:
-
Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Mannque Rho et al., Introduction to The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710, pdf)
Original articles
-
Kanabu Nawa, Hideo Suganuma, Toru Kojo, Brane-induced Skyrmions: Baryons in Holographic QCD, Prog.Theor.Phys.Suppl.168:231-236, 2007 (arXiv:hep-th/0701007)
-
Hovhannes R. Grigoryan, Baryon as skyrmion-like soliton from the holographic dual model of QCD, talk at From Strings to Things 2008 (pdf)
-
Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
-
Stefano Bolognesi, Paul Sutcliffe, The Sakai-Sugimoto soliton, JHEP 1401:078, 2014 (arXiv:1309.1396)
-
Paul Sutcliffe, Holographic Skyrmions, Mod. Phys. Lett. B29 (2015) no. 16, 1540051 (spire:1383608)
Nucleons
nucleon form factors via holographic QCD:
-
Kiminad A. Mamo, Ismail Zahed, Nucleon mass radii and distribution: Holographic QCD, Lattice QCD and GlueX data (arXiv:2103.03186)
-
Roldão da Rocha, Information entropy of nuclear electromagnetic transitions in AdS/QCD [arXiv:2208.07191]
The derived parameters are shown to corroborate experimental data with great accuracy
via a nuclear matrix model:
-
Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
nuclear binding energy
- Salvatore Baldino, Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Holographic Nuclear Physics with Massive Quarks (arXiv:2102.00680)
nuclear binding energy via the nuclear matrix model:
- Koji Hashimoto, Yoshinori Matsuo, Nuclear binding energy in holographic QCD (arXiv:2103.03563)
Pentaquarks
- Kazuo Ghoroku, Akihiro Nakamura, Tomoki Taminato, Fumihiko Toyoda, Holographic Penta and Hepta Quark State in Confining Gauge Theories, JHEP 1008:007,2010 (arxiv:1003.3698)
Parton distribution functions
- Matteo Rinaldi, Double parton correlations in mesons within AdS/QCD soft-wall models: a first comparison with lattice data (arXiv:2003.09400)
Heavy flavor in holographic QCD
Discussion of heavy flavor in holographic QCD:
-
Yizhuang Liu, Ismail Zahed, Heavy and Strange Holographic Baryons, Phys. Rev. D 96, 056027 (2017) (arXiv:1705.01397)
-
Si-wen Li, A holographic description of heavy-flavoured baryonic matter decay involving glueball, Phys. Rev. D 99, 046013 (2019) (arXiv:1812.03482)
(via additional flavor branes)
-
Nicolas Kovensky, Andreas Schmitt, Heavy Holographic QCD (arxiv:1911.08433)
-
Daisuke Fujii, Atsushi Hosaka, Heavy baryons in holographic QCD with higher dimensional degrees of freedom (arXiv:2003.13415)
(via higher KK-modes)
-
Yidian Chen, Mei Huang, Holographic QCD model for (arXiv:2110.08215)
Flux string breaking
- Oleg Andreev, String Breaking, Baryons, Medium, and Gauge/String Duality (arXiv:2003.09880)
Glueball physics
-
Kenji Suzuki, D0-D4 system and , Phys.Rev. D63 (2001) 084011 (arXiv:hep-th/0001057)
-
S.S. Afonin, A.D. Katanaeva, Glueballs and deconfinement temperature in AdS/QCD (arXiv:1809.07730)
-
S. S. Afonin, A. D. Katanaeva, E. V. Prokhvatilov, M. I. Vyazovsky, Deconfinement temperature in AdS/QCD from the spectrum of scalar glueballs (arXiv:2001.07990)
-
Cornélio Rodrigues Filho, Glueballs in the Klebanov-Strassler Theory: Pseudoscalars vs Scalars (arXiv:2011.12689)
Holographic Schwinger effect
Interpretation in holographic QCD of the Schwinger effect of vacuum polarization as exhibited by the DBI-action on flavor branes:
Precursor computation in open string theory:
- Constantin Bachas, Massimo Porrati, Pair Creation of Open Strings in an Electric Field, Phys. Lett. B296 (1992) 77-84 (arXiv:hep-th/9209032)
Relation to the DBI-action of a probe brane in AdS/CFT:
-
Gordon Semenoff, Konstantin Zarembo, Holographic Schwinger Effect, Phys. Rev. Lett. 107, 171601 (2011) (arXiv:1109.2920, doi:10.1103/PhysRevLett.107.171601)
-
S. Bolognesi, F. Kiefer, E. Rabinovici, Comments on Critical Electric and Magnetic Fields from Holography, J. High Energ. Phys. 2013, 174 (2013) (arXiv:1210.4170)
-
Yoshiki Sato, Kentaroh Yoshida, Holographic description of the Schwinger effect in electric and magnetic fields, J. High Energ. Phys. 2013, 111 (2013) (arXiv:1303.0112)
-
Yoshiki Sato, Kentaroh Yoshida, Holographic Schwinger effect in confining phase, JHEP 09 (2013) 134 (arXiv:1306.5512
-
Yoshiki Sato, Kentaroh Yoshida, Universal aspects of holographic Schwinger effect in general backgrounds, JHEP 12 (2013) 051 (arXiv:1309.4629)
-
Daisuke Kawai, Yoshiki Sato, Kentaroh Yoshida, The Schwinger pair production rate in confining theories via holography, Phys. Rev. D 89, 101901 (2014) (arXiv:1312.4341)
-
Yue Ding, Zi-qiang Zhang, Holographic Schwinger effect in a soft wall AdS/QCD model (arXiv:2009.06179)
Relation to DBI-action of flavor branes in holographic QCD:
-
Koji Hashimoto, Takashi Oka, Vacuum Instability in Electric Fields via AdS/CFT: Euler-Heisenberg Lagrangian and Planckian Thermalization, JHEP 10 (2013) 116 (arXiv:1307.7423)
-
Koji Hashimoto, Takashi Oka, Akihiko Sonoda, Magnetic instability in AdS/CFT: Schwinger effect and Euler-Heisenberg Lagrangian of Supersymmetric QCD, J. High Energ. Phys. 2014, 85 (2014) (arXiv:1403.6336)
-
Koji Hashimoto, Shunichiro Kinoshita, Keiju Murata, Takashi Oka, Electric Field Quench in AdS/CFT, J. High Energ. Phys. 2014 (arXiv:1407.0798)
-
Koji Hashimoto, Takashi Oka, Akihiko Sonoda, Electromagnetic instability in holographic QCD, J. High Energ. Phys. 2015, 1 (2015) (arXiv:1412.4254)
See also:
-
Xing Wu, Notes on holographic Schwinger effect, J. High Energ. Phys. 2015, 44 (2015) (arXiv:1507.03208, doi:10.1007/JHEP09(2015)044)
-
Kazuo Ghoroku, Masafumi Ishihara, Holographic Schwinger Effect and Chiral condensate in SYM Theory, J. High Energ. Phys. 2016, 11 (2016) (doi:10.1007/JHEP09(2016)011)
-
Le Zhang, De-Fu Hou, Jian Li, Holographic Schwinger effect with chemical potential at finite temperature, Eur. Phys. J. A54 (2018) no.6, 94 (spire:1677949, doi:10.1140/epja/i2018-12524-4)
-
Wenhe Cai, Kang-le Li, Si-wen Li, Electromagnetic instability and Schwinger effect in the Witten-Sakai-Sugimoto model with D0-D4 background, Eur. Phys. J. C 79, 904 (2019) (doi:10.1140/epjc/s10052-019-7404-1)
-
Zhou-Run Zhu, De-fu Hou, Xun Chen, Potential analysis of holographic Schwinger effect in the magnetized background (arXiv:1912.05806)
-
Zi-qiang Zhang, Xiangrong Zhu, De-fu Hou, Effect of gluon condensate on holographic Schwinger effect, Phys. Rev. D 101, 026017 (2020) (arXiv:2001.02321)
Review:
-
Daisuke Kawai, Yoshiki Sato, Kentaroh Yoshida, A holographic description of the Schwinger effect in a confining gauge theory, International Journal of Modern Physics A Vol. 30, No. 11, 1530026 (2015) (arXiv:1504.00459)
-
Akihiko Sonoda, Electromagnetic instability in AdS/CFT, 2016 (spire:1633963, pdf)
Application to vector meson dominance
Derivation of vector meson dominance via holographic QCD:
-
D.T. Son, M.A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182)
-
Sungho Hong, Sukjin Yoon, Matthew Strassler, On the Couplings of Vector Mesons in AdS/QCD, JHEP 0604 (2006) 003 (arXiv:hep-th/0409118)
-
Sungho Hong, Sukjin Yoon, Matthew Strassler, On the Couplings of the Rho Meson in AdS/QCD (cds:816440, arXiv:hep-ph/0501197)
-
Leandro Da Rold, Alex Pomarol, Chiral symmetry breaking from five dimensional spaces, Nucl. Phys. B721:79-97, 2005 (arXiv:hep-ph/0501218)
and specifically in the Witten-Sakai-Sugimoto model:
- Tadakatsu Sakai, Shigeki Sugimoto, p. 18 and Section 5 of: More on a holographic dual of QCD, Progr. Theor. Phys. 114: 1083-1118, 2005 (arXiv:hep-th/0507073)
Application to the quark-gluon plasma
Application to the quark-gluon plasma:
Expositions and reviews include
-
Pavel Kovtun, Quark-Gluon Plasma and String Theory, RHIC news (2009) (blog entry)
-
Makoto Natsuume, String theory and quark-gluon plasma (arXiv:hep-ph/0701201)
-
Steven Gubser, Using string theory to study the quark-gluon plasma: progress and perils (arXiv:0907.4808)
-
Francesco Biagazzi, A. Cotrone, Holography and the quark-gluon plasma, AIP Conference Proceedings 1492, 307 (2012) (doi:10.1063/1.4763537, slides pdf)
-
Brambilla et al., section 9.2.2 of QCD and strongly coupled gauge theories - challenges and perspectives, Eur Phys J C Part Fields. 2014; 74(10): 2981 (doi:10.1140/epjc/s10052-014-2981-5)
Holographic discussion of the shear viscosity of the quark-gluon plasma goes back to
- Giuseppe Policastro, D.T. Son, A.O. Starinets, Shear viscosity of strongly coupled supersymmetric Yang-Mills plasma, Phys. Rev. Lett.87:081601, 2001 (arXiv:hep-th/0104066)
Other original articles include:
-
Brett McInnes, Holography of the Quark Matter Triple Point (arXiv:0910.4456)
-
Hovhannes R. Grigoryan, Paul M. Hohler, Mikhail A. Stephanov, Towards the Gravity Dual of Quarkonium in the Strongly Coupled QCD Plasma (arXiv:1003.1138)
-
Mansi Dhuria, Aalok Misra, Towards MQGP, JHEP 1311 (2013) 001 (arXiv:1306.4339)
-
Irina Ya. Aref’eva, Kristina Rannu, Pavel Slepov, Energy Loss in Holographic Anisotropic Model for Heavy Quarks in External Magnetic Field (arXiv:2012.05758)
See also:
-
Si-wen Li, Yi-peng Zhang, Correlation function of fundamental fermion in holographic QCD [arXiv:2307.13357]
-
Nelson R. F. Braga, Octavio C. Junqueira, Hawking-Page transition in holographic QCD at finite density [arXiv:2404.04683]
Application to lepton anomalous magnetic moment
Application to anomalous magnetic moment of the muon:
-
Luigi Cappiello, What does Holographic QCD predict for anomalous ?, 2015 (pdf)
-
Josef Leutgeb, Anton Rebhan, Axial vector transition form factors in holographic QCD and their contribution to the anomalous magnetic moment of the muon (arXiv:1912.01596)
-
Josef Leutgeb, Anton Rebhan, Axial vector transition form factors in holographic QCD and their contribution to the muon (arXiv:2012.06514)
-
Josef Leutgeb, Jonas Mager, Anton Rebhan, Holographic QCD and the muon anomalous magnetic moment (arXiv:2110.07458)
Application to the Higgs field
Application to the Higgs field:
-
Domenec Espriu, Alisa Katanaeva, Composite Higgs Models: a new holographic approach (arXiv:1812.01523)
-
Johanna Erdmenger, Nick Evans, Werner Porod, Konstantinos Rigatos, Gauge/gravity dual dynamics for the strongly coupled sector of composite Higgs models, JHEP 58 (2021) [arXiv:2010.10279, doi:10.1007/JHEP02(2021)058]
Application to -angle axions and strong CP-problem
Realization of axions and solution of strong CP-problem:
- Francesco Bigazzi, Alessio Caddeo, Aldo L. Cotrone, Paolo Di Vecchia, Andrea Marzolla, The Holographic QCD Axion (arXiv:1906.12117)
Discussion of the theta angle via the the graviphoton in the higher WZW term of the D4-brane:
- Si-wen Li, around (3.1) of The theta-dependent Yang-Mills theory at finite temperature in a holographic description (arXiv:1907.10277)
Discussion of the Witten-Veneziano mechanism
- Josef Leutgeb, Anton Rebhan, Witten-Veneziano mechanism and pseudoscalar glueball-meson mixing in holographic QCD (arxiv:1909.12352)
See also:
- Si-wen Li, Hao-qian Li, Yi-peng Zhang, The worldvolume fermion as baryon in holographic QCD with a theta angle [arXiv:2402.01197]
Application to the QCD trace anomaly
Discussion of the QCD trace anomaly:
-
Jose L. Goity, Roberto C. Trinchero, Holographic models and the QCD trace anomaly, Phys. Rev. D 86, 034033 – 2012 (arXiv:1204.6327)
-
Aalok Misra, Charles Gale, The QCD Trace Anomaly at Strong Coupling from M-Theory (arXiv:1909.04062)
The QCD trace anomaly affects notably the equation of state of the quark-gluon plasma, see there at References – Holographic description of quark-gluon plasma
Application to parton distribution
- Akira Watanabe, Takahiro Sawada, Mei Huang, Extraction of gluon distributions from structure functions at small x in holographic QCD (arxiv:1910.10008)
Understanding the nucleon structure is one of the most important research topics in fundamental science, and tremendous efforts have been done to deepen our knowledge over several decades. Since are highly nonperturbative physical quantities, in principle they are not calculable by the direct use of QCD. Furthermore, although there is available data, this has large errors. These facts cause the huge uncertainties which can be seen in the preceding studies based on the global QCD analysis.
In this work, we investigate the gluon distribution in nuclei by calculating the structure functions in the framework of holographic QCD, which is constructed based on the AdS/CFT correspondence.
Application to QCD phases
- R. Narayanan, H. Neuberger, A survey of large continuum phase transitions, PoSLAT 2007:020, 2007 (arXiv:0710.0098)
- Kazem Bitaghsir Fadafan, Jesus Cruz Rojas, Nick Evans, A Holographic Description of Colour Superconductivity, Phys. Rev. D 98 (2018) 066010 [arXiv:1803.03107, doi:10.1103/PhysRevD.98.066010]
to confinement/deconfinement phase transiton:
- Meng-Wei Li, Yi Yang, Pei-Hung Yuan Imprints of Early Universe on Gravitational Waves from First-Order Phase Transition in QCD (arXiv:1812.09676)
With magnetic fields:
- Umut Gursoy, Holographic QCD and magnetic fields (arXiv:2104.02839)
Of relevance in neutron stars:
-
Carlos Hoyos, Niko Jokela, Matti Jarvinen, Javier G. Subils, Javier Tarrio, Aleksi Vuorinen, Transport in strongly coupled quark matter, Phys.Rev.Lett. 125 (2020) 241601 (arXiv:2005.14205)
-
Carlos Hoyos, Niko Jokela, Matti Järvinen, Javier G. Subils, Javier Tarrio, Aleksi Vuorinen, Holographic approach to transport in dense QCD matter, Phys.Rev.D 105 (2022) 6, 066014 (arXiv:2109.12122)
-
Matti Järvinen, Holographic modeling of nuclear matter and neutron stars, Eur.Phys.J.C. 56 2021 (arXiv:2110.08281)
-
Carlos Hoyos, Niko Jokela, Aleksi Vuorinen, Holographic approach to compact stars and their binary mergers, Prog.Part.Nucl.Phys. 126 (2022) 103972 (arXiv:2112.08422)
See also
-
Yosuke Imamura, Baryon Mass and Phase Transitions in Large N Gauge Theory, Prog. Theor. Phys. 100 (1998) 1263-1272 (arxiv:hep-th/9806162)
-
Varun Sethi, A study of phases in two flavour holographic QCD (arXiv:1906.10932)
-
Riccardo Argurio, Matteo Bertolini, Francesco Bigazzi, Aldo L. Cotrone, Pierluigi Niro, QCD domain walls, Chern-Simons theories and holography, J. High Energ. Phys. (2018) 2018: 90 (arXiv:1806.08292)
-
Alfonso Ballon-Bayona, Jonathan P. Shock, Dimitrios Zoakos, Magnetic catalysis and the chiral condensate in holographic QCD (arXiv:2005.00500)
-
Yi Yang, Pei-Hung Yuan, QCD Phase Diagram by Holography (arXiv:2011.11941)
-
Nicolas Kovensky, Aaron Poole, Andreas Schmitt, Phases of cold holographic QCD: baryons, pions and rho mesons [arXiv:2302.10675]
Application to meson physics
Application to meson physics:
-
Daniel Ávila, Leonardo Patiño, Melting holographic mesons by cooling a magnetized quark gluon plasma (arXiv:2002.02470)
-
Xuanmin Cao, Hui Liu, Danning Li, Pion quasiparticles and QCD phase transitions at finite temperature and isospin density from holography, Phys. Rev. D 102, 126014 (2020) (arXiv:2009.00289)
-
Xuanmin Cao, Songyu Qiu, Hui Liu, Danning Li, Thermal properties of light mesons from holography (arXiv:2102.10946)
Application to quarkonium:
-
Hovhannes R. Grigoryan, Paul M. Hohler, Mikhail A. Stephanov, Towards the Gravity Dual of Quarkonium in the Strongly Coupled QCD Plasma (arXiv:1003.1138)
-
Rico Zöllner, Burkhard Kampfer, Holographic vector meson melting in a thermal gravity-dilaton background related to QCD (arXiv:2002.07200)
-
Miguel Angel Martin Contreras, Saulo Diles, Alfredo Vega, Heavy quarkonia spectroscopy at zero and finite temperature in bottom-up AdS/QCD (arXiv:2101.06212)
Application of holographic QCD to B-meson physics and flavour anomalies
Application of holographic QCD (holographic light front QCD) to B-meson physics and flavour anomalies:
-
Ruben Sandapen, Mohammad Ahmady, Predicting radiative B decays to vector mesons in holographic QCD (arXiv:1306.5352)
-
Mohammad Ahmady, R. Campbell, S. Lord, Ruben Sandapen, Predicting the form factors using AdS/QCD Distribution Amplitudes for the meson, Phys. Rev. D88 (2013) 074031 (arXiv:1308.3694)
-
Mohammad Ahmady, Dan Hatfield, Sébastien Lord, Ruben Sandapen, Effect of resonances in the branching ratio and forward-backward asymmetry of the decay
-
Mohammad Ahmady, Alexandre Leger, Zoe McIntyre, Alexander Morrison, Ruben Sandapen, Probing transition form factors in the rare decay, Phys. Rev. D 98, 053002 (2018) (arXiv:1805.02940)
-
Mohammad Ahmady, Holographic light-front QCD in B meson phenomenology, PoS DIS2013 (2013) 182 (arXiv:2001.00266)
Relation to holographic entanglement entropy
Relating to holographic entanglement entropy:
- Zhibin Li, Kun Xu, Mei Huang, The entanglement properties of holographic QCD model with a critical end point (arXiv:2002.08650)
Application to defects
Application to QCD with defects:
- Alexander Gorsky, Valentin Zakharov, Ariel Zhitnitsky, On Classification of QCD defects via holography, Phys. Rev. D79:106003, 2009 (arxiv:0902.1842)
Application to thermal QCD
-
Vikas Yadav, Aalok Misra, Towards Thermal QCD from M theory at Intermediate ‘t Hooft Coupling and G-Structure Classification of Non-supersymmetric Underlying Geometries (arXiv:2004.07259)
-
Alfonso Ballon-Bayona, Luis A. H. Mamani, Alex S. Miranda, Vilson T. Zanchin, Effective holographic models for QCD: Thermodynamics and viscosity coefficients (arXiv:2103.14188)
-
Qingxuan Fu, Song He, Li Li, Zhibin Li, Revisiting holographic model for thermal and dense QCD with a critical point [arXiv:2404.12109]
Last revised on April 22, 2024 at 03:46:38. See the history of this page for a list of all contributions to it.