nLab D8-brane

Idea

The D-brane in type II string theory of dimension $8+1$.

Properties

As black branes in massive IIA supergravity

As black brane-solutions, D8-branes appear in massive type IIA supergravity (“Romans supergravity”)/massive type IIA string theory

(Bergshoess-de Roo-Green-Papadopoulos-Townsend 96, Chamblin-Perry 97, Janssen-Meessen-Ortin 99)

Since the normal n-sphere around a D8-brane (with its 9-dimensional worldvolume) in 10-dimensional spacetime is a 0-sphere, D8-brane charge is measured by the RR-field 0-flux form $F_0$. This behaves like a cosmological constant in the corresponding D=10 supergravity (“Romans supergravity”). Its presences changes ordinary type IIA string theory to what is called massive type IIA string theory, whose relation to the web of dualities in string theory remains not well understood. In particular the duality between type IIA string theory and M-theory remains ill-understood for massive type IIA string theory.

Bound states

For the bound states and brane intersections involving D8-branes, see at

• D4-D8-brane bound states

• D6-D8-brane bound states

As geometric engineering of flavour physics

In geometric engineering of flavor physics in intersecting D-brane models, the flavour degrees of freedom come from open strings ending on spacetime-filling D-branes (Karch-Katz 02).

Specifically in the Sakai-Sugimoto model geometrically engineering something close to actual quantum chromodynamics (Sakai-Sugimoto 04, Sakai-Sugimoto 05), flavour is encoded in the presence of D8-branes in the model:

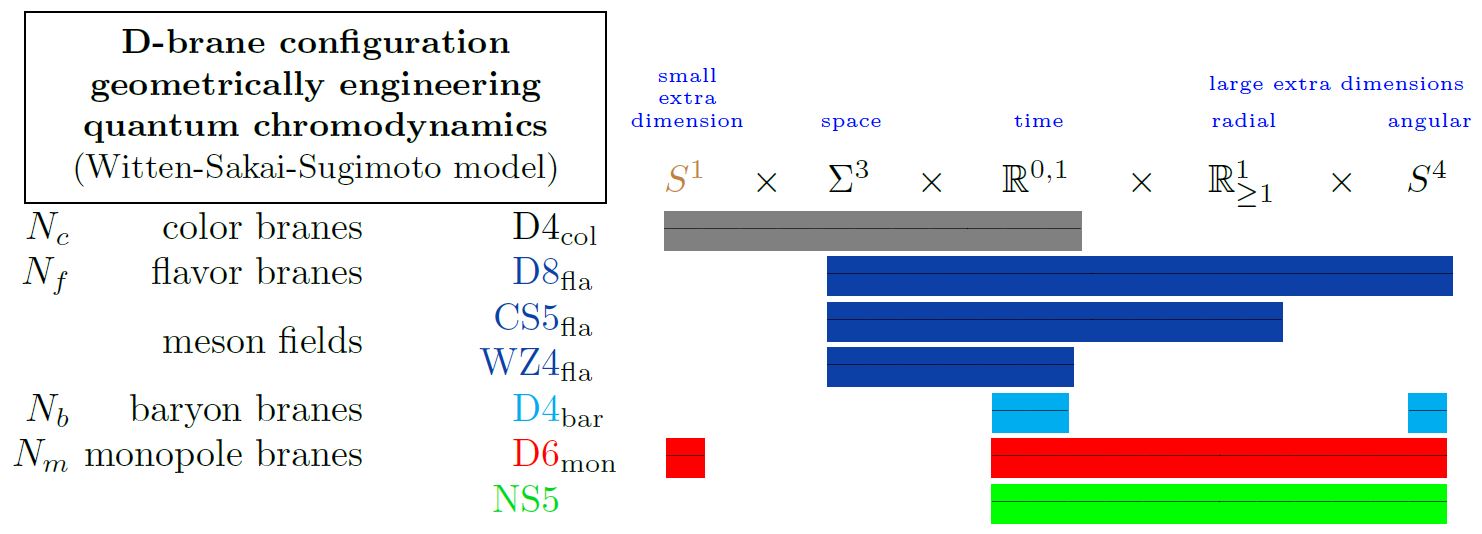
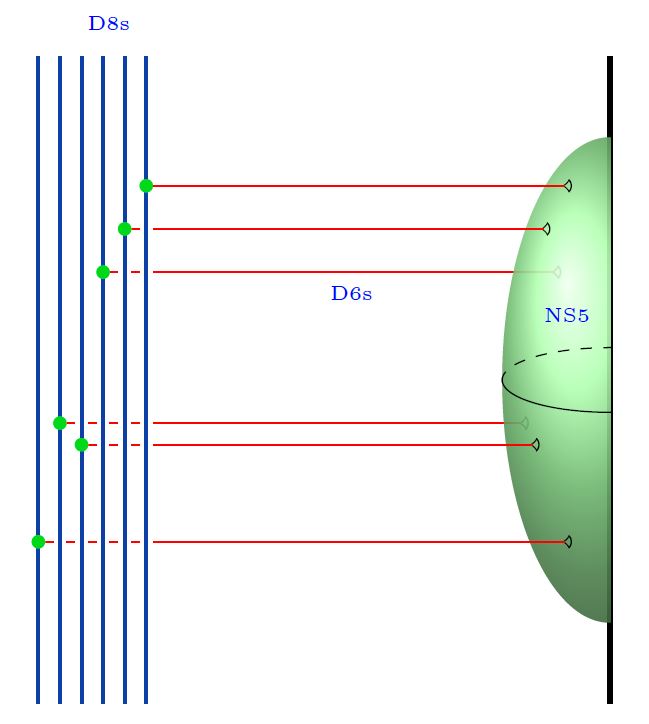
Here we are showing

1. the color D4-branes;

2. the flavor D8-branes;

   with

   1. the 5d Chern-Simons theory on their worldvolume

   2. the corresponding 4d WZW model on the boundary

   both exhibiting the meson fields;

3. the baryon D4-branes

   (see at WSS-model – Baryons);

4. the Yang-Mills monopole D6-branes

   (see at D6-D8-brane bound state);

5. the NS5-branes (often not considered here).

Related concepts

• D4-D8 brane bound state

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

brane	in supergravity	charged under gauge field	has worldvolume theory
black brane	supergravity	higher gauge field	SCFT
D-brane	type II	RR-field	super Yang-Mills theory
$(D = 2n)$	type IIA	$\,$	$\,$
D(-2)-brane	$\,$	$\,$
D0-brane	$\,$	$\,$	BFSS matrix model
D2-brane	$\,$	$\,$	$\,$
D4-brane	$\,$	$\,$	D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane	$\,$	$\,$	D=7 super Yang-Mills theory
D8-brane	$\,$	$\,$
$(D = 2n+1)$	type IIB	$\,$	$\,$
D(-1)-brane	$\,$	$\,$	$\,$
D1-brane	$\,$	$\,$	2d CFT with BH entropy
D3-brane	$\,$	$\,$	N=4 D=4 super Yang-Mills theory
D5-brane	$\,$	$\,$	$\,$
D7-brane	$\,$	$\,$	$\,$
D9-brane	$\,$	$\,$	$\,$
(p,q)-string	$\,$	$\,$	$\,$
(D25-brane)	(bosonic string theory)
NS-brane	type I, II, heterotic	circle n-connection	$\,$
string	$\,$	B2-field	2d SCFT
NS5-brane	$\,$	B6-field	little string theory
D-brane for topological string			$\,$
A-brane			$\,$
B-brane			$\,$
M-brane	11D SuGra/M-theory	circle n-connection	$\,$
M2-brane	$\,$	C3-field	ABJM theory, BLG model
M5-brane	$\,$	C6-field	6d (2,0)-superconformal QFT
M9-brane/O9-plane			heterotic string theory
M-wave
topological M2-brane	topological M-theory	C3-field on G₂-manifold
topological M5-brane	$\,$	C6-field on G₂-manifold
S-brane
SM2-brane, membrane instanton
M5-brane instanton
D3-brane instanton
solitons on M5-brane	6d (2,0)-superconformal QFT
self-dual string		self-dual B-field
3-brane in 6d

References

As black brane solutions

As a black brane the D8 was identified as a solution to Romans supergravity/massive type IIA string theory in

• Eric Bergshoeff, Mees de Roo, Michael Green, George Papadopoulos, Paul Townsend, Duality of Type II 7-branes and 8-branes, Nucl. Phys. B 470 (1996) 113-135 [arXiv:hep-th/9601150]

See also

• A. Chamblin, Malcolm Perry, Dynamic D8-branes in IIA string theory (arXiv:hep-th/9712112)

• Bert Janssen, Patrick Meessen, Tomas Ortin, The D8-brane tied up: String and brane solutions in massive type IIA supergravity, Phys. Lett. B453 (1999) 229-236 (spire:494174, doi:10.1016/S0370-2693(99)00315-9)

On D6-D8-brane bound states in massive type IIA string theory:

• Harvendra Singh, Duality symmetric massive type II theories in $D=8$ and $D=6$, JHEP 0204:017, 2002 (arXiv:hep-th/0109147)

• Harvendra Singh, Note on (D6,D8) Bound State, Massive Duality and Non-commutativity, Nucl. Phys. B661 (2003) 394-408 (arXiv:hep-th/0212103)

• Fabio Apruzzi, Marco Fazzi, Dario Rosa, Alessandro Tomasiello, All $AdS_7$ solutions of type II supergravity, JHEP 04 (2014) 064 (arxiv:1309.2949)

As geometric engineering of flavor physics

geometric engineering of flavour physics on spacetime-filling D-branes in intersecting D-brane models (AdS/QCD) was originally understood in

• Andreas Karch, Emanuel Katz, Adding flavor to AdS/CFT, JHEP 0206:043, 2002 (arxiv:hep-th/0205236)

and then developed in detail for QCD via D8-branes in the Sakai-Sugimoto model:

• Tadakatsu Sakai, Shigeki Sugimoto, Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)

• Tadakatsu Sakai, Shigeki Sugimoto, More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)

Relation to K-theory

The role of the D8 in the K-theory-classification of D-branes is discussed in

• John Schwarz, sections 6.2 and 6.3 of TASI Lectures on Non-BPS D-Brane Systems (arXiv:hep-th/9908144)

• Ion V. Vancea, On the Algebraic K-theory of The Massive D8 and M9 Branes, Int. J. Mod. Phys. A16 (2001) 4429-4452 (arXiv:hep-th/9905034)

Lift to M-theory

A lift of D8-branes to M-theory M-branes by generalized Scherk-Schwarz reduction, relating to D7-branes in F-theory, is proposed in

• Chris Hull, Massive String Theories From M-Theory and F-Theory, JHEP 9811:027, 1998 (arXiv:hep-th/9811021)

Relation of heterotic M-theory to type I' string theory with D8-branes at O8-planes, via a sequence of dualities in string theory:

• Ofer Aharony, Zohar Komargodski, Assaf Patir, The Moduli Space and M(atrix) Theory of 9d $\mathcal{N} =1$ Backgrounds of M/String Theory (arXiv:hep-th/0702195)