nLab hadron Kaluza-Klein theory
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
The idea of Kaluza-Klein theory has traditionally been applied mostly to “color physics”, such as in attempts to realize the color charges of quantum chromodynamics (quarks and gluons) as a Kaluza-Klein compactification of heterotic supergravity (see for instance at string phenomenology – heterotic models). The success of this approach remains somewhat elusive (see also at landscape of string theory vacua).
Alternatively, Kaluza-Klein theory may be considered for “flavor physics” to produce the charges of flavor-“hidden local symmetries”, namely the baryons and mesons, respectively, hence the hadrons of quantum hadrodynamics. In terms of geometric engineering of QFT via intersecting D-brane models this means to consider gauge theory on flavor branes (instead of on color branes), such as in the Witten-Sakai-Sugimoto model of holographic QCD.
| color charge | flavor charge | |
|---|---|---|
| gauge bosons | gluons (gauge group-local symmetry) | mesons (flavor-hidden local symmetry) |
| fermions | quarks | baryons |
Indeed, the experimentally observed mesons appear in towers of increasing mass (“higher resonances”), which may usefully be identified as a Kaluza-Klein tower of the single gauge boson of an SU(2)-D=5 Yang-Mills theory (Son-Stephanov 03).
Moreover, the pion field appears as the gauge 0-mode of this tower, right away in its solitonic incarnation as the Skyrmion-excitation in 4d, hence reflecting baryons. (This phenomenon is secretly the old theorem of Atiyah-Manton 89, as explained from the modern perspective of holographic QCD in Sutcliffe 10, Sutcliffe 15).
Various qualitative phenomena of the phenomenology of quantum hadrodynamics find a natural explanation in hadron Kaluza-Klein theory this way, notably:
-
hidden local symmetry itself (by the very KK-reduction of a gauge theory)
-
vector meson dominance (as discussed there)
-
QCD sum rules (…)
-
(…)
In terms of string phenomenology, the flavor brane-D=5 Yang-Mills theory which gives quantum hadrodynamics this way naturally arises on D4/D8-brane intersections in the Witten-Sakai-Sugimoto model (Sakai-Sugimoto 04, Sakai-Sugimoto 05) or else on M5-branes wrapped on a closed interval (Ivanova-Lechtenfeld-Popov 18)
Already to first approximation, this produces for instance baryon mass spectra with moderate quantitative agreement with experiment (HSSY 07):
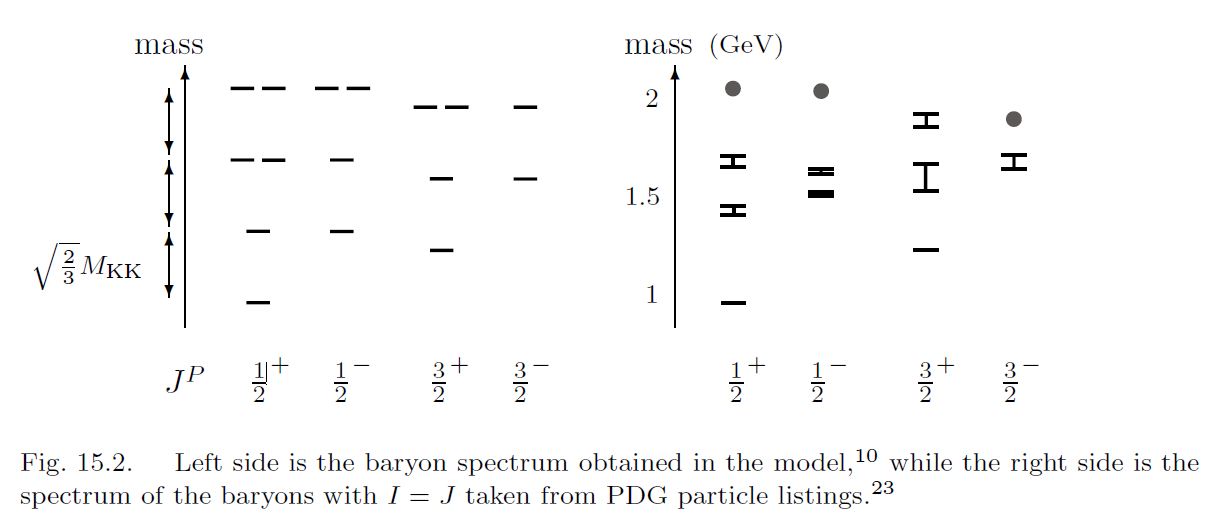
graphics grabbed from Sugimoto 16
An extensive review of hadron Kaluza-Klein theory may be found in Rho et al 16.
Strikingly, the experimentally observed hadron-spectrum also exhibits supersymmetry: see at hadron supersymmetry.
Related concepts
References
Hadrons as KK-modes of 5d Yang-Mills theory
The suggestion that the tower of observed vector mesons – when regarded as gauge fields of hidden local symmetries of chiral perturbation theory – is reasonably modeled as a Kaluza-Klein tower of D=5 Yang-Mills theory:
- D. T. Son, M. A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182, doi:10.1103/PhysRevD.69.065020)
That the pure pion-Skyrmion-model of baryons is approximately the KK-reduction of instantons in D=5 Yang-Mills theory is already due to:
- Michael Atiyah, Nicholas Manton, Skyrmions from instantons, Phys. Lett. B, 222(3):438–442, 1989 (doi:10.1016/0370-2693(89)90340-7)
with a hyperbolic space-variant in:
- Michael Atiyah, Paul Sutcliffe, Skyrmions, instantons, mass and curvature, Phys. Lett. B605 (2005) 106-114 (arXiv:hep-th/0411052)
Further discussion of this approximation:
- Josh Cork, Chris Halcrow, ADHM skyrmions (arXiv:2110.15190)
The observation that the result of Atiyah-Manton 89 becomes an exact Kaluza-Klein construction of Skyrmions/baryons from D=5 instantons when the full KK-tower of vector mesons as in Son-Stephanov 03 is included into the Skyrmion model (see also there) is due to:
-
Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
-
Paul Sutcliffe, Holographic Skyrmions, Mod. Phys. Lett. B29 (2015) no. 16, 1540051 (spire:1383608, doi:10.1142/S0217984915400515)
In the Sakai-Sugimoto model of holographic QCD the D=5 Yang-Mills theory of this hadron Kaluza-Klein theory is identified with the worldvolume-theory of D8-flavour branes intersected with D4-branes in an intersecting D-brane model:
-
Tadakatsu Sakai, Shigeki Sugimoto, section 5.2 of Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, section 3.3. of More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)
-
Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, Shinichiro Yamato, Baryons from instantons in holographic QCD, Prog.Theor.Phys.117:1157, 2007 (arXiv:hep-th/0701280)
-
Stefano Bolognesi, Paul Sutcliffe, The Sakai-Sugimoto soliton, JHEP 1401:078, 2014 (arXiv:1309.1396)
-
Lorenzo Bartolini, Stefano Bolognesi, Andrea Proto, From the Sakai-Sugimoto Model to the Generalized Skyrme Model, Phys. Rev. D 97 014024 (2018) [doi:10.1103/PhysRevD.97.014024, arXiv:1711.03873]
-
Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Tommaso Rainaldi, Mass and Isospin Breaking Effects in the Skyrme Model and in Holographic QCD [arXiv:2312.15404]
Extensive review of this holographic/KK-theoretic-realization of quantum hadrodynamics from D=5 Yang-Mills theory is in:
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific, Second edition, 2016 (doi:10.1142/9710)
- Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Via the realization of D4/D8 brane bound states as instantons in the D8-brane worldvolume-theory (see there and there), this relates also to the model of baryons as wrapped D4-branes, originally due to
-
Edward Witten, Baryons And Branes In Anti de Sitter Space, JHEP 9807:006, 1998 (arXiv:hep-th/9805112)
-
David Gross, Hirosi Ooguri, Aspects of Large Gauge Theory Dynamics as Seen by String Theory, Phys. Rev. D58:106002, 1998 (arXiv:hep-th/9805129)
and further developed in the nuclear matrix model:
-
Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
In relation to Yang-Mills monopoles:
- Stefano Bolognesi, Solitons, Large and Holography, 2015 (pdf)
Discussion, in this context, of D-term effects affecting hadron stability:
- Mitsutoshi Fujita, Yoshitaka Hatta, Shigeki Sugimoto, Takahiro Ueda, Nucleon D-term in holographic QCD arXiv:2206.06578
More on baryons in the Sakai-Sugimoto model of holographic QCD:
- Salvatore Baldino, Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Holographic Nuclear Physics with Massive Quarks, Phys. Rev. D 103 126015 (2021) [doi:10.1103/PhysRevD.103.126015, arXiv:2102.00680]
More on mesons in holographic QCD:
-
Johanna Erdmenger, Nick Evans, Ingo Kirsch, Ed Threlfall, Mesons in Gauge/Gravity Duals - A Review, Eur. Phys. J. A 35 (2008) 81-133 [arXiv:0711.4467, doi:10.1140/epja/i2007-10540-1]
-
Daniel Ávila, Leonardo Patiño, Melting holographic mesons by cooling a magnetized quark gluon plasma (arXiv:2002.02470)
-
Xuanmin Cao, Hui Liu, Danning Li, Pion quasiparticles and QCD phase transitions at finite temperature and isospin density from holography, Phys. Rev. D 102, 126014 (2020) (arXiv:2009.00289)
-
Xuanmin Cao, Songyu Qiu, Hui Liu, Danning Li, Thermal properties of light mesons from holography (arXiv:2102.10946)
-
Artur Amorim, Miguel S. Costa, Matti Järvinen, Regge theory in a Holographic dual of QCD in the Veneziano Limit (arXiv:2102.11296)
-
Roldão da Rocha, Information in AdS/QCD: mass spectroscopy of isovector mesons, Phys. Rev. D 103 106027 (2021) [arXiv:2103.03924, doi:10.1103/PhysRevD.103.106027]
-
Shahin Mamedov, Narmin Nasibova, Temperature dependence of meson-nucleon coupling constant from the soft-wall model (arXiv:2103.10494)
An alternative scenario of derivation of 4d Skyrmions by KK-compactification of D=5 Yang-Mills theory, now on a closed interval, motivated by M5-branes instead of by D4/D8-brane intersections as in the Sakai-Sugimoto model, is discussed in:
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Skyrme model from 6d theory, Physics Letters B Volume 783, 10 August 2018, Pages 222-226 (arXiv:1805.07241)
following
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Non-Abelian sigma models from Yang-Mills theory compactified on a circle, Physics Letters B Volume 781, 10 June 2018, Pages 322-326 (arXiv:1803.07322)
See also:
- Y. H. Ahn, Sin Kyu Kang, Hyun Min Lee, Towards a Model of Quarks and Leptons (arXiv:2112.13392)
History
The late Michael Atiyah, following up on his visionary early work in Atiyah-Manton 89, saw the relevance of further develop hadron Kaluza-Klein theory, and suggested using advanced tools of complex geometry for this purpose; for a reminiscence see
- Bernd Schroers, p. 2-3 of: Michael Atiyah and Physics: the Later Years, (arXiv:1910.10630) in: Notices of the AMS, Memories of Sir Michael Atiyah (pdf)
This led to a sequence of visionary but speculative articles, including the following:
-
Michael Atiyah, Nicholas Manton, Bernd Schroers, Geometric Models of Matter, Proceedings of the Royal Society A (arXiv:1108.5151, doi:10.1098/rspa.2011.0616)
-
Michael Atiyah, Nicholas Manton, Complex Geometry of Nuclei and Atoms, International Journal of Modern Physics AVol. 33, No. 24, 1830022 (2018) (arXiv:1609.02816, doi:10.1142/S0217751X18300223)
-
Michael Atiyah, Geometric Models of Helium, Modern Physics Letters AVol. 32, No. 14, 1750079 (2017) (arXiv:1703.02532, doi:10.1142/S0217732317500791)
The idea here is to try to match patterns in the characteristic classes (Chern classes) of complex surfaces to properties of nuclei.
Created on May 8, 2020 at 12:00:05. See the history of this page for a list of all contributions to it.