nLab non-perturbative quantum field theory

Contents

Context

Physics

Idea
Related concepts
References

Idea

The description of quantum field theory is traditionally mostly considered only in the infinitesimal neighbourhood of the underlying classical and free field theory As such these descriptions are referred to as perturbative quantum field theory (pQFT) since they describe only small (in fact: infinitesimal) “perturbations” of a (hypothetical) free and classical field, instead of the fully interacting quantum fields.

Since this very coarse (but remarkably successful) perturbative concept of quantum field theory has come to often be considered by default, one speaks of non-perturbative quantum field theory in order to amplify that the full theory is meant to be considered, not just the perturbative approximation.

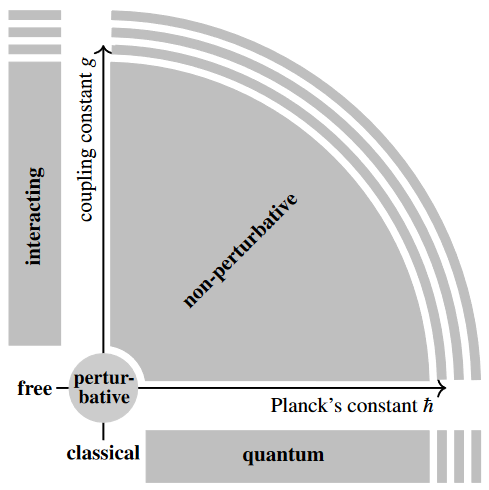
Beyond the infinitesimal neighbourhood of perturbation theory. More concretely, if we think of generic (Lagrangian) quantum field theories as parameterized by

Planck's constant $\;\hbar$ ,

expressing the “strength of quantum effects”,
coupling constants $\;g$ ,

expressing the strength of interactions of fields,

then perturbative QFT is concerned (just) with computing the Feynman perturbation series for scattering amplitudes as (just) a formal power series in these variables, and since this typically has a vanishing radius of convergence (see there) it concerns just the infinitesimal neighbourhood of the origin in this parameter space (the infinitesimal halo of a single point) – all the rest of the parameter space is the region of non-perturbative quantum field theory.

As perturbation with non-perturbative effects. Passage from the perturbative to the non-perturbative description of QFT involves taking account of non-perturbative effects invisible to perturbation theory.

These arise notably from the presence of solitonic field configurations (instantonic, after Wick rotation): Such solitonic fields are invisible to perturbation theory because they are not continuously connected to the vacuum field configuration, since they are constituted by topologically non-trivial structures, e.g. gauge potentials which are connections on a topologically non-trivial principal bundle on spacetime (such as Dirac monopoles or Yang-Mills instantons, see at fiber bundles in physics).

In lack of a general prescription for non-perturbative quantization, authors try to make educated guesses about the would-be non-perturbative effects from inspection of the behaviour of the formal Feynman perturbation series: popular methods here go by the name Borel resummation and resurgence theory.

Theory and reality. Beware the usual habit in theoretical physics jargon of conflating the map with the territory (the field theory with the actual fields “in nature” that the theory means to describe): Real quantum fields in nature are always non-perturbative (the value of $\hbar$ and $g$ is not contained in the infinitesimal neightbourhood of the origin – this is a purely theoretical/computational concept) so that their description by perturbative QFT is, by design, just an approximation of their complete nature.

As non-analyticity. This is just as with smooth functions and their description by their Taylor series of their derivatives at a given origin: The Taylor series is a “perturbative description” of the full smooth function, which in contrast is the full non-perturbative object. Indeed the Feynman perturbation series in pQFT are imagined to be just such Taylor series of actual smooth functions (e.g. scattering amplitudes) in $\hbar$ and $g$ , and the goal of non-perturbative QFT is to provide more information on “non-perturbative effects”, hence on the actual functions (scattering amplitudes) at all or at least some positive values of $\hbar$ and/or $g$ .

Of course, special among all smooth functions are the analytic functions, whose Taylor series does already capture the full function, at least in some open neighbourhood. Accordingly, among QFTs that one can write to paper (but which are unlikely to describe anything in the real world) there are interacting examples (cite…) whose perturbative description already exhausts their full non-perturbative content, in that their Feynman perturbation series actually converges, or at least has a positive radius of convergence.

Axiomatization and construction. Among axiomatizations of non-perturbative field theory is

algebraic quantum field theory (AQFT) in terms of local nets of observables with values in $C^\ast$ -algebras (axiomatizing the Heisenberg picture of quantum physics),
functorial quantum field theory in terms of cobordism category representations (axiomatizing the Schrödinger picture of quantum physics).

Among construction methods of AQFT has been “constructive field theory”, which aims to make rigorous analytic sense of path integrals in simple cases. This has worked for scalar field theory such as $\phi^4$ -theory in spacetime dimension 2 and 3, but (so far) not in dimension 4.

There are also some partial tools available from quantum mechanics such as strict deformation quantization (Rieffel 1989). Here it may be noteworthy that the established construction of perturbative quantum field theory has been understood to be an example of the systematic process of quantization called formal deformation quantization, specifically as an example of Fedosov deformation quantization (Collini 16). Since the non-perturbative version of formal deformation quantization is strict C*-algebraic deformation quantization the latter might be a useful perspective on the problem of non-perturbative QFT (cf. e.g. SS23).

Examples of nonperturbative QFT. Presently, non-perturbative quantum field theories have been constructed only for simple toy examples, notably:

for free field theories (no interaction),
in low spacetime dimension (e.g. 2d CFTs, see e.g. at conformal net),
for topological quantum field theories (see e.g. at quantization of 3d Chern-Simons theory),
for pure scalar field theory (most famously $\phi^4$ -theory, cf. Serone 2018)

(Examples of non-perturbative interacting scalar field theory in any spacetime dimension are claimed in Buchholtz & Fredenhagen 2020, at least in the guise of local nets of quantum observables, pending the construction (or existence) of compatible vacuum states).

Key application: Confinement/Mass-gap in QCD/Yang-Mills. A non-perturbative effect of paramount importance in experimentally observed quantum physics (and invisible to perturbative QCD) is the confinement and the mass gap of quantum chromodynamics (Yang-Mills theory with simple gauge group).

That this experimentally observed confinement mechanism is indeed somehow encoded in the Lagrangian density for the gluons and quarks of QCD is plausibly verfied currently (only) by computer simulation (lattice QCD), but an analytic construction of a corresponding non-perturbative quantization of Yang-Mills theory has remained elusive enough to be pronounced one of the open “Millennium Problems” by the Clay Mathematics Institute (see there).

However, qualitative understanding of confinement is given by an argument that separated quarks become connected by flux tubes of the strong nuclear force field, which behave like strings whose string-tension exerts an attractive force on any pair of quarks, keeping them together and hence “confined” inside a hadron bound state.

The attempt to understand non-perturbative confined QCD and hence quantum hadrodynamics as a theory of such flux tube strings has been both the origin of string theory as well as, after some detour through GUT quantum gravity, its current understanding via the holographic principle: See at Polyakov gauge-string duality, at AdS/QCD correspondence and at confinement via AdS/QCD.

However, ironically also string theory has been mostly understood only in perturbation theory, which currently causes the approach of holographic QCD to require the assumption of a large (in fact: humongous) and hence unrealistic number of quark colors (namely of color branes).

But for this string theory, at least, there are hints as to its non-perturbative completion, enough so that it has a working title (“M-theory”) albeit remaining elusive. See at AdS-CFT correspondence – small- $N$ corrections for more on this.

Related concepts

References

(See also references at non-perturbative effect, soliton and instanton, particularly at Yang-Mills instanton.)

General introduction:

Alexander P. Bakulev, Dmitry Shirkov, Inevitability and Importance of Non-Perturbative Elements in Quantum Field Theory, Proceedings of the 6th Mathematical Physics Meeting, Sept. 14–23 (2010) Belgrade, Serbia 27–54 [arXiv:1102.2380, ISBN:978-86-82441-30-4]

Monographs:

Yitzhak Frishman, Jacob Sonnenschein: Non-Perturbative Field Theory – From Two Dimensional Conformal Field Theory to QCD in Four Dimensions, Cambridge University Press (2010) [doi:10.1017/CBO9780511770838, summary: arXiv:1004.4859].
open access (2023) [doi:10.1017/9781009401654]

“Relativistic Quantum Field Theory has been very successful in describing strong, electro-magnetic and weak interactions, in the region of small couplings by using perturbation theory, within the framework of the Standard Model. However, the region of strong coupling, like the hadronic spectrum and various scattering phenomena of hadrons within QCD, is still largely unsolved. A large variety of methods have been used to address this question, including QCD sum rules, lattice gauge simulations, light cone quantization, low energy effective Lagrangians like the Skyrme model and chiral Lagrangians, large $N$ approximation, techniques of conformal invariance, integrable model approach, supersymmetric models, string theory approach etc. In spite of this major effort the gap between the phenomenology and the basic theory has been only partially bridged, and the problem is still open. The goals of this book are to provide a detailed description of the tool box of nonperturbative techniques, to apply them on simplified systems, mainly of gauge dynamics in two dimensions, and to examine the lessons one can learn from those systems about four dimensional QCD and hadron physics.”

and via Wightman axioms:

Franco Strocchi, An Introduction to Non-Perturbative Foundations of Quantum Field Theory, Oxford University Press (2013) [doi:10.1093/acprof:oso/9780199671571.001.0001]

“The perturbative series is known to diverge, and actually, for the prototypic model of self-interacting scalar field ( $\phi^4$ -theory), on which most of the textbooks are based, the perturbative expansion is misleading, since the theory has been proved to be trivial in $s+1$ dimensions (with $s \geq 3$ ). Clearly, this makes it difficult to define a QFT through its perturbative expansion and raises conceptual problems such as the mathematical consistency of such an expansion. As a matter of fact, after more than fifty years of QFT we are still in the embarrassing situation of not knowing a single non-trivial (even non-realistic) model of QFT in 3+1 dimensions, allowing a non-perturbative control.”

Collections:

Gerard ’t Hooft, Arthur Jaffe, Gerhard Mack, P. K. Mitter, Raymond Stora (eds.) Nonperturbative Quantum Field Theory, NATO Science Series B 185 (1988) [doi:10.1007/978-1-4613-0729-7]
Jürg Fröhlich, Non-perturbative quantum field theory – Mathematical Aspects and Applications, Advanced Series in Mathematical Physics, World Scientific (1992) [doi:10.1142/1245]

Outlook from the point of view of causal perturbation theory/locally covariant perturbative quantum field theory:

Stefan Hollands, Robert Wald, section 4.1 of: Quantum fields in curved spacetime, Physics Reports 574 (2015) 1-35 [arXiv:1401.2026, doi:10.1016/j.physrep.2015.02.001]

The case of scalar field theory (such as $\phi^n$ -theory):

Marco Serone, from 2:46 on in A look at $\phi^4_2$ using perturbation theory (January 2018) [recording&
Detlev Buchholz, Klaus Fredenhagen, A $C^\ast$ -algebraic approach to interacting quantum field theories, Commun. Math. Phys. 377 (2020) 947–969 [arXiv:1902.06062, doi:10.1007/s00220-020-03700-9]