nLab duality in physics
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Duality
-
abstract duality: opposite category,
-
concrete duality: dual object, dualizable object, fully dualizable object, dualizing object
Examples
-
between higher geometry/higher algebra
-
Langlands duality, geometric Langlands duality, quantum geometric Langlands duality
In QFT and String theory
Contents
Idea
In fundamental physics, notably in quantum field theory and string theory one often says that a non-trivial equivalence of quantum field theories between two models (in theoretical physics) is a “duality”.
Examples
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
Formalization and Relation to mathematical duality
One should beware that the use of the word “duality” in physics is in general different from concepts called “duality” in mathematics.
For instance in T-duality only simple cases exhibit such obviously “dual” behaviour and in general cases such as U-duality really only the notion of equivalence remains. This more closely resembles the mathematical concept of Morita equivalence, see Relation to Morita equivalence. However, in some cases such as Montonen-Olive duality/S-duality the equivalence involves some actual duality in the mathematical sense, as in replacing the gauge group by its Langlands dual group.
General formulation
One way to accurately formalize most of what is usually meant by “duality” in physics might instead be the following.
Write for a moduli stack of prequantum field theory data consisting of species of fields and of Lagrangians/action functionals defined on these.
Example
For the well-understood case of mirror symmetry this would be the usual moduli space of Calabi-Yau manifolds regarded as the Lagrangian data for the 2d (2,0)-superconformal QFT.
One imagines that quantization gives a map from such prequantum data to a moduli stack of actual quantum field theories
Example
Continuing example in the case of mirror symmetry this would be the TCFT-construction that takes a Calabi-Yau manifold to its Calabi-Yau A-∞ category (“of branes”) which defines the corresponding 2d TQFT via the noncompact version of the cobordism hypothesis.
The 1-image of this map would be the moduli space of Lagrangian quantum field theories
By assumption this is now a 1-epimorphism and hence an atlas of moduli stacks.
The physical concept of duality, such as in mirror symmetry, says that two points in the space of Lagrangian data are “dual” to each other, if they become equivalent as quantum field theories after quantization.
Mathematically this means that the space of such “dualities” is the homotopy fiber product
By definition, an element of is two Lagrangians and a choice of equivalence of their associated quantum field theories:
This construction is the first step in associating the groupoid object in an (∞,1)-category which is induced by the atlas “quantization” via Giraud's theorem of Higher Topos Theory.
It continues in the way that Cech covers do (whence one speaks of the Cech nerve construction of the quantization map ): above “” there is the space of triples of Lagrangian data that all have the same quantization, equipped with dualities between any two of them, and equipped with an equivalence of dualities (hence a “duality of dualities”) between the composite of two of these and the third:
It continues this way through all -fold dualities of dualities. The resulting -groupoid object has as moduli stack of objects and as moduli stack of 1-morphisms . Its corresponding stack realization is and so the corresponding augmented simplicial object looks as
Such towers are to be thought of as the incarnation of equivalence relations as we pass to (∞,1)-category theory: A plain equivalence relation is just the first stage of such a tower
The conditions on an equivalence relation – reflexivity, transitivity, symmetry – may be read as those on a groupoid object – identity, composition, inverses. So now in homotopy logic this is boosted to an groupoid object in an (∞,1)-category by relaxing all three to hold only up to higher coherent homotopies.
The bottom-most arrow
is the quotient projection of the equivalence relation. In 1-logic this would be its cokernel, here in homotopy logic it is the homotopy colimit over the full simplicial diagram.
So the perspective of the full diagram gives the usual way of speaking in QFT also a reverse:
instead of saying
a) that two Lagrangians are dual if there is an equivalence between the QFTs which they induce under quantization,
we may turn this around and say that therefore
b) quantization is the result of forming the homotopy quotient of the space of Lagrangian data by these duality relations.
It is one of the clauses of the Giraud theorem in (∞,1)-topos theory that these two perspectives are equivalent.
Examples
For a concrete example of the above, consider the class of Chern-Simons theories and Rozansky-Witten theories. As Lagrangian field theories they are very different, but after perturbative quantization, their Lagrangian data maps to the same abstract vector space of quantum observables: the Vassiliev knot invariants.
Concretely, in both cases the map from Lagrangian data to quantum observables is given by the assignment of weight systems on Jacobi diagrams, namely:
1) Lie algebra weight systems for Chern-Simons theory
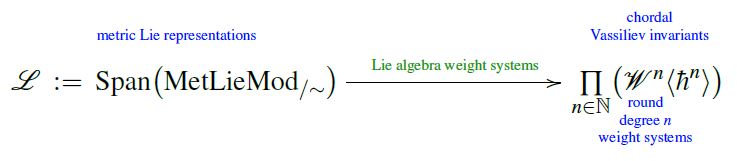
2) Rozansky-Witten weight systems for Rozansky-Witten theory
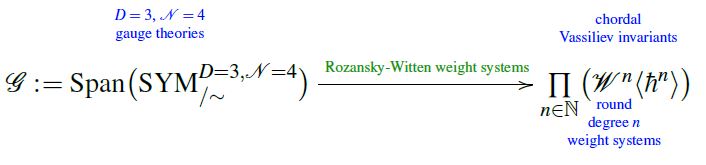
The corresponding Wilson loop quantum observables are the evaluation of these weight systems on the universal Vassiliev invariant
1) Chern-Simons theory Wilson loop observables:

2) Rozansky-Witten theory Wilson loop observables:

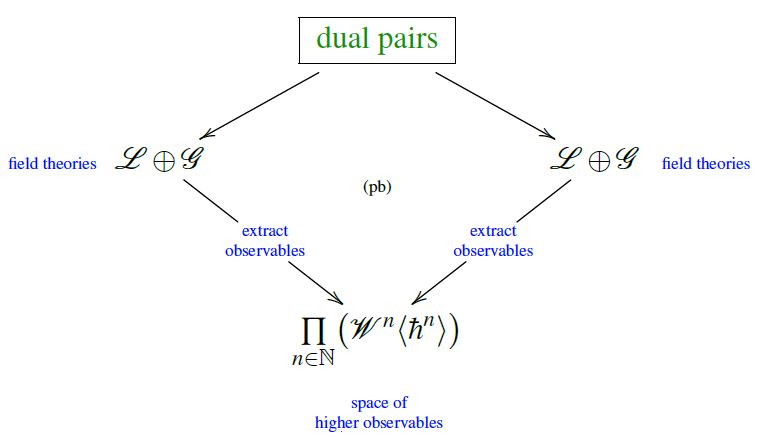
Hence in total we have the following quantization map from Lagrangian data to observables:

To the extent that all observables of these theories, on the 3-sphere, are Wilson loop observables, we must regard as physically equivalent any two elements on the left of this map (Lagrangian field theories) whose image on the right coincides. The space of such pairs is the fiber product of this quantization map with itself:
Relation to Morita equivalence
According to Schwarz 04:
I am convinced that the mathematical notion of Morita equivalence of associative algebras and its generalization for differential associative algebras should be regarded as the mathematical foundation of dualities in string/M-theory.
Schwarz showed that KK-compactifications on Morita equivalent noncommutative tori are physically equivalent (Schwarz98). This work is followed up in relation to T-duality in Pioline99 and CNS11.
BMRS08 discusses an axiomatic definition of topological T-duality generalizing and refining T-duality between noncommutative spaces in terms of Morita equivalence to a special type of KK-equivalence, which defines a T-duality action that is of order two up to Morita equivalence.
In Okada09 a variant of mirror symmetry is shown to be a form of derived Morita equivalence.
Morita theoretic ideas are also involved in factorization homology, the blob complex and premodular TQFTS, see MW10, BZBJ15, and Scheimbauer for the Morita -category of -algebras.
Duality after compactification
Informal comments on a possible general picture of duality in physics arising from duality in string theory, especially after KK-compactification, from Brennan, Carta & Vafa 17, p. 7:
Since we have seen that the full string theories are all interrelated by a sequence of dualities, one would expect that their compactifications are also related by dualities. As it turns out, these relations are so abundant that we can make the following observation:
“Conjecture”: Whenever the dimension, number of preserved supercharges, and chiralities of two different compactifications of string theory match, there are choices of compactification geometries such that they are dual descriptions of the same physical theory.
Surprisingly, we are aware of no known counter examples. In this sense, dualities in lower dimensional theories are not hard to find, but rather are hard to prevent! One rationale for the existence of dualities is as Sergio Cecotti puts it, “the scarcity of rich structures”. In particular the very existence of quantum systems of gravity is hard to arrange and if we succeed to get more than one theory with a given symmetry, there is a good chance we have landed on the same theory.
Related concepts
There is also a duality in the description of physics:
duality between algebra and geometry
in physics:
References
General
-
Luis Alvarez-Gaumé, Frederic Zamora, Duality in Quantum Field Theory (and String Theory), AIP Conference Proceedings 423, 46 (1998) (arXiv:hep-th/9709180)
-
David Corfield, Duality as a category-theoretic concept, Studies in History and Philosophy of Modern Physics Volume 59, August 2017, Pages 55-61 (doi:10.1016/j.shpsb.2015.07.004)
As Morita equivalence
On the idea that duality in physics may be captured by the notion of Morita equivalence:
-
Albert Schwarz, Morita equivalence and duality (arXiv:hep-th/9805034)
-
B. Pioline, Albert Schwarz, Morita equivalence and T-duality (or versus ) (arXiv:hep-th/9908019)
See also
- Albert Schwarz, My Life In Science, 2004 (pdf, pdf)
Specifically concerning T-duality:
-
Ee Chang-Young, Hiroaki Nakajima, Hyeonjoon Shin, Fermionic T-duality and Morita Equivalence (arXiv:1101.0473)
-
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-branes, KK-theory and duality on noncommutative spaces, (pdf)
Specifically concerning mirror symmetry:
- So Okada, Homological mirror symmetry of Fermat polynomials (arXiv:0910.2014)
See also more general discussion of Morita equivalence:
-
David Ben-Zvi, Adrien Brochier, David Jordan, Integrating quantum groups over surfaces: quantum character varieties and topological field theory, (arXiv:1501.04652)
-
Scott Morrison, Kevin Walker, The blob complex, (arXiv:1009.5025)
-
Claudia Scheimbauer, Factorization Homology as a Fully Extended Topological Field Theory, (pdf)
Duality in string theory
On duality in string theory (but see there fore more):
-
Joseph Polchinski, Dualities (arXiv:1412.5704)
-
Cumrun Vafa, around 3:30, 12:00 of On Mathematical Aspects of String Theory (video)
Last revised on July 9, 2023 at 15:56:31. See the history of this page for a list of all contributions to it.