nLab category

This page is about the concept in mathematics. For the concept of the same name in philosophy see at category (philosophy).

Idea

• A category consists of a collection of things and binary relationships (or transitions) between them, such that these relationships can be combined and include the “identity” relationship “is the same as.”

• A category is a quiver (a directed graph with multiple edges) with a rule saying how to compose two edges that fit together to get a new edge. Furthermore, each vertex has an edge starting and ending at that vertex, which acts as an identity for this composition.

• A category is a combinatorial model for a directed space – a “directed homotopy 1-type” in some sense. It has “points”, called objects, and also directed “paths”, or “processes” connecting these points, called morphisms. There is a rule for how to compose paths; and for each object there is an identity path that starts and ends there.

• More precisely, a category consists of a collection of objects and a collection of morphisms. Every morphism has a source object and a target object. If $f$ is a morphism with $x$ as its source and $y$ as its target, we write

  $$f : x \to y$$

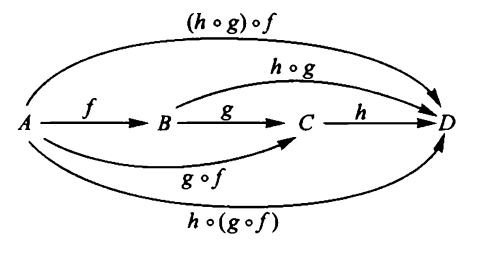
  and we say that $f$ is a morphism from $x$ to $y$. In a category, we can compose a morphism $g : x \to y$ and a morphism $f : y \to z$ to get a morphism $f \circ g : x \to z$. Composition is associative and satisfies the left and right unit laws.

A good example to keep in mind is the category Set, in which the objects are sets and a morphism $f : x \to y$ is a function from the set $x$ to the set $y$. Here composition is the usual composition of functions.

For more background on and context for categories see

• category theory.

Definitions

There are two broad ways to write down the definition of category; in the usual foundations of mathematics, these two definitions are equivalent. It is good to know both, for several reasons:

• Each introduces its own system of notation, both of which are useful in other parts of category theory, so one should know them.

• One definition generalises quite nicely to the notion of internal category, while the other generalises quite nicely to the notion of enriched category; these are both important concepts.

• When examining alternative foundations, sometimes one definition or the other may be more appropriate; in any case, one will want to examine the question of their equivalence.

The two definitions may be distinguished by whether they use a single collection of all morphisms or several collections of morphisms, a family of collections indexed by pairs of objects.

With one collection of morphisms

[Grothendieck 61, Section 4]

A category $C$ consists of

• a collection (see Foundational issues and Size issues) $C_0$ of objects;

• a collection $C_1$ of morphisms (or arrows);

• for every morphism $f$, an object $s(f)$ (called its source or domain), and an object $t(f)$ (called its target or codomain);

• for every pair of morphisms $f$ and $g$, where $t(f) = s(g)$, a morphism $g \circ f$, called their composite (also written $g f$ or sometimes $f;g$— see diagrammatic order);

• for every object $x$, a morphism $id_x$ (or $1_x$), called the identity morphism on $x$;

• such that the following properties are satisfied:

  • source and target are respected by composition: $s(g \circ f) = s(f)$ and $t(g\circ f) = t(g)$;

  • source and target are respected by identities: $s(1_x) = x$ and $t(1_x) = x$;

  • composition is associative: $(h \circ g)\circ f = h\circ (g \circ f)$ whenever $t(f) = s(g)$ and $t(g) = s(h)$;

  • composition satisfies the left and right unit laws: if $s(f) = x$ and $t(f) = y$, then $1_y \circ f = f = f \circ 1_x$.

People also often write $x \in C$ instead of $x \in C_0$ as a short way to indicate that $x$ is an object of $C$. Also, some people write $Ob(C)$ and $Mor(C)$ instead of $C_0$ and $C_1$. One usually writes $f\colon x \to y$ if $f \in C_1$ to state that $s(f) = x$ and $t(f) = y$. Finally, people often write $hom(x,y)$, $hom_C(x,y)$, or $C(x,y)$ for the collection of morphisms $f\colon x \to y$.

If the identity-assigning map and its axiom is omitted, then one speaks of a semicategory.

With a family of collections of morphisms

A category $C$ consists of

• a collection (see Foundational issues and Size issues) $C_0$ of objects;

• for each pair $x,y$ of objects, a collection $C_1(x,y)$ of morphisms from $x$ to $y$;

• for each pair of morphisms $f$ in $C_1(x,y)$ and $g$ in $C_1(y,z)$, a morphism $g \circ f$ in $C_1(x,z)$, called their composite (also written $g f$ or sometimes $f;g$— see diagrammatic order);

• for each object $x$, a morphism $id_x$ (or $1_x$) in $C_1(x,x)$, called the identity morphism on $x$;

• such that the following properties are satisfied:

  • composition is associative: for each quadruple $w,x,y,z$ of objects, if $f \in C_1(y,z)$, $g \in C_1(x,y)$, and $h \in C_1(w,x)$, then $(f \circ g)\circ h = f\circ (g \circ h)$;

  • composition satisfies the left and right unit laws: for each pair $x,y$ of objects, if $f \in C_1(x,y)$, then $1_y \circ f = f = f \circ 1_x$.

People also often write $x \in C$ instead of $x \in C_0$ as a short way to indicate that $x$ is an object of $C$. Also, some people write $Ob(C)$ instead of $C_0$ and $hom(x,y)$, $hom_C(x,y)$, or $C(x,y)$ instead of $C_1(x,y)$. One usually writes $f\colon x \to y$ to state that $f \in C_1(x,y)$. Finally, people often write $C_1$ or $Mor(C)$ for the disjoint union $\biguplus_{x \in C_0} \biguplus_{y \in C_0} C_1(x,y)$.

Equivalence between the two definitions

Given a one-collection-of-morphisms category $C_1\rightrightarrows C_0$, we define a family-of-collections-of-morphisms category by taking $C_1(x,y)$ to be the preimage of $(x,y)$ under the function $(s,t):C_1 \to C_0\times C_0$. Conversely, given a family-of-collections-of-morphisms category we define a one-collection-of-morphisms category by taking $C_1$ to be the disjoint union of the families of morphisms $C_1 = \coprod_{x,y\in C_0} C_1(x,y)$. With the straightforward definitions of functor and natural transformation in both cases, this sets up a strict 2-equivalence? of 2-categories.

Note, though, that this 2-equivalence is not an isomorphism of 2-categories, because the disjoint union operation has to “tag” each morphism with its domain and codomain. It seems that the strongest thing that can be said is that, in a material set theory, if a family-of-collections-of-morphisms category $C$ has the property that sets $C_1(x,y)$ are all disjoint, then there is a one-collection-of-morphisms category with $C_1 = \bigcup_{x,y\in C_0} C_1(x,y)$ (the non-disjoint union) that gives rise to $C$ on the nose. The notion of protocategory is a way to formalize a family-of-collections-of-morphisms category together with the information about how its hom-sets “overlap”.

In ordinary category theory one rarely specifies which of the two definitions is being used, although often language implicitly suggests that it is the latter, e.g. when defining a category one first specifies the objects and then specifies what “the morphisms from $X$ to $Y$ are” rather than specifying what “a morphism” is and then what the domain and codomain of each morphism are. Indeed, when defining a category in this way, one rarely worries about whether the hom-sets are disjoint, meaning that it must be the second definition in use. Even for the prototypical category Set, if constructed in a material-set-theoretic foundation like ZFC, the natural definition “a morphism from $X$ to $Y$ is a function, i.e. a subset of $X\times Y$ that is total and functional”, produces hom-sets that are not disjoint, since a total and functional set of ordered pairs can have any codomain that is a superset of its range. Moreover, categorical constructions do not “naturally” preserve disjointness of homsets, e.g. in the category of elements $el(P)$ of a functor $P:C\to Set$ a given morphism in $C$ can “be” a morphism between many different elements of $P$, and similarly for a slice category and so on.

Foundational issues

We said a category has a ‘collection’ of objects and ‘collection’(s) of morphisms. However, different mathematical foundations have different notions of equality. For foundations whose notion of ‘collection’ have proposition-valued equality, such as in set theory, class-set theory, or extensional type theory, the two definitions above suffice for defining a category. However, in for other foundations, with a weaker notion of equality, such as internally in a (2,1)-topos like Grpd, in Thomas Streicher‘s groupoid model of types, or in homotopy type theory, there are multiple definitions of a category. The naive definition of the category above with a collection of objects and a collection of morphisms results in a wild category. If the morphism collections are sets, then the resulting structure is a precategory, and if the collection of objects is a set as well, then the resulting structure is a strict category. The above definitions in set theory foundations are the same as strict categories in the alternative foundations, but in the alternative foundations categories like Set are not strict categories. Instead, they happen to be a special kind of precategory called univalent categories, where equality of objects is isomorphism of objects.

Size issues

We said a category has a ‘collection’ of objects and ‘collection’(s) of morphisms. A category is said to be small if these collections are all sets — as opposed to proper classes, for example. (The alternatives depend on ones foundations for mathematics.)

Similarly, a category is locally small if $C_1(x,y)$ is a set for every pair of objects $x,y$ in that category. The most common motivating examples of categories (such as Set) are all locally small but not small (unless one restricts their objects in some way).

Alternative definitions

For some purposes it is useful or necessary to vary the way the ordinary definition of category is expressed. See

• single-sorted definition of a category– a variant of the first definition, with only one collection at all ($C_1$, no $C_0$). This is sometimes convenient for technical reasons.

• type-theoretic definition of category– a variant of the second definition, interpreted explicitly in dependent type theory.

• protocategory– a sort of mixture of the two definitions, in which all the hom-sets $C_1(x,y)$ are subsets of a single set $C_1$, but not necessarily disjoint.

Equivalent definitions

A category is equivalently

• a monad in the 2-category of spans of sets;

• a monoid in the monoidal category of endospans on the set of objects;

• a simplicial set which satisfies the Segal conditions;

• a simplicial set which satisfies the weak Kan complex conditions strictly:

• hence a directed homotopy type which is “1-truncated”

Generalizations

Internal categories

The first definition, with a single collection $C_1$ of morphisms, generalises to the notion of internal category. Essentially, we define a category internal to (some other category) $D$ as above, with ‘collection’ interpreted as an object of $D$ and ‘function’ interpreted as a morphism of $D$. In particular, a category internal to Set is the same thing as a small category.

Enriched categories

The second definition of a category, as a family $C_1(x,y)$ of collections of morphisms, generalises to the notion of enriched category: we define a category enriched over (some other category) $D$ as above, with the collection of objects still a ‘collection’ as before, but with objects of $D$ in place of the collections of morphisms and morphisms of $D$ in place of the various functions. In particular, a category enriched over Set is the same thing as a locally small category.

Indexed categories

The notion of indexed category captures the idea of woking “over a base” other than Set.

Multicategories etc.

There is a generalization of the notion of category where one allows a morphism to go from several objects to a single object. This is called a multicategory or operad. If we additionally allow a morphism to go to several objects, we obtain a polycategory or PROP.

Higher categories

See higher category theory.

Examples

There is the beginning of a database of categories listing well-known categories (with links to articles on these categories, if such articles exist) and some of their properties.

The classic example of a category is Set, the category with sets as objects and functions as morphisms, and the usual composition of functions as composition. Here are some other famous examples, which arise as variations on this theme:

• Vect - vector spaces as objects, linear maps as morphisms.

• Grp - groups as objects, homomorphisms as morphisms.

• Top - topological spaces as objects, continuous functions as morphisms.

• Diff - smooth manifolds as objects, smooth maps as morphisms.

• Ring - rings as objects, ring homomorphisms as morphisms.

Note that in all these cases the morphisms are actually special sorts of functions. these are concrete categories. That need not be the case in general!

These classic examples are the original motivation for the term “category”: all of the above categories encapsulate one “kind of mathematical structure”. These are often called “concrete” categories (that term also has a technical definition that these examples all satisfy). But just as widespread in applications as these categorization examples of categories are are other categories (often “small” ones) which, roughly, model something like states and processes of some system.

• Poset A poset can be thought of as a category with its elements as objects and one morphism in each $hom(x,y)$ if $x$ is less than or equal to $y$, but none otherwise.

• Group A group is just a category where there’s one object and all the morphisms have inverses - we call the morphisms “elements” of the group. This may seem weird, but it’s actually a very useful viewpoint. Here’s another way to say it: A group is a groupoid with a single object.

• Monoid More generally, a monoid is a category with a single object. In fact, this is one way to motivate the concept of categories: categories are the many object version of monoids.

• Groupoid A groupoid is a category in which all morphisms are isomorphisms.

• Quiver A quiver may be identified with the free category on its directed graph. Given a directed graph $G$ with collection of vertices $G_0$ and collection of edges $G_1$, there is the free category $F(G)$ on the graph whose collection of objects coincides with the collection of vertices, and whose collection of morphisms consists of finite sequences of edges in $G_1$ that fit together head-to-tail. The composition operation in this free category is the concatenation of sequences of edges.

• Universal structure A category bearing a structure making it initial (or 2-initial) in some doctrine. Examples include the permutation category as the free symmetric monoidal category generated by a single object, or the simplex category which is initial among monoidal categories equipped with a monoid.

Basic notions

A homomorphism between categories is a functor.

This way small categories themselves form a category, the category Cat whose objects are small categories and whose morphisms are functors. This naturally enhances to a 2-category whose 2-morphisms are natural transformations between functors.

An equivalence of categories is an equivalence in Cat, hence a pair of functors going back and forth, that are each others inverse up to natural isomorphism.

Weaker than the notion of a pair of functors exhibiting an equivalence is the notion of a pair of adjoint functors.

Other standard operations on categories include

• opposite category

• localization

• geometric realization of categories

Related concepts

• enriched category

  • continuous category

• EI-category

• 0-category, (0,1)-category

• category

  semicategory

• 2-category

• 3-category

• n-category

• (∞,0)-category

• (n,1)-category

• (∞,1)-category

• (∞,2)-category

• (∞,n)-category

• (n,r)-category

algebraic structure	oidification
magma	magmoid
pointed magma with an endofunction	setoid/Bishop set
unital magma	unital magmoid
quasigroup	quasigroupoid
loop	loopoid
semigroup	semicategory
monoid	category
anti-involutive monoid	dagger category
associative quasigroup	associative quasigroupoid
group	groupoid
flexible magma	flexible magmoid
alternative magma	alternative magmoid
absorption monoid	absorption category
cancellative monoid	cancellative category
rig	CMon-enriched category
nonunital ring	Ab-enriched semicategory
nonassociative ring	Ab-enriched unital magmoid
ring	ringoid
nonassociative algebra	linear magmoid
nonassociative unital algebra	unital linear magmoid
nonunital algebra	linear semicategory
associative unital algebra	linear category
C-star algebra	C-star category
differential algebra	differential algebroid
flexible algebra	flexible linear magmoid
alternative algebra	alternative linear magmoid
Lie algebra	Lie algebroid
monoidal poset	2-poset
strict monoidal groupoid?	strict (2,1)-category
strict 2-group	strict 2-groupoid
strict monoidal category	strict 2-category
monoidal groupoid	(2,1)-category
2-group	2-groupoid/bigroupoid
monoidal category	2-category/bicategory

References

(For more extensive references see at category theory.)

The concept originates in

• Samuel Eilenberg, Saunders MacLane, General Theory of Natural Equivalences, Transactions of the American Mathematical Society 58 2 (1945) 231-294 [doi:10.1090/S0002-9947-1945-0013131-6, jstor:1990284]

The definition “with a single set of morphisms” (i.e. as internal categories in Set) appears in:

• Alexander Grothendieck, Section 4 of: Techniques de construction et théorèmes d’existence en géométrie algébrique III: préschémas quotients, Séminaire Bourbaki: années 1960/61, exposés 205-222, Séminaire Bourbaki, no. 6 (1961), Exposé no. 212, (numdam:SB_1960-1961__6__99_0, pdf)

Textbook accounts:

• Saunders MacLane, Categories for the Working Mathematician, Graduate Texts in Mathematics 5, Springer (1971, second ed. 1997) [doi:10.1007/978-1-4757-4721-8]

• Francis Borceux, Handbook of Categorical Algebra, Encyclopedia of Mathematics and its Applications 50, Cambridge University Press (1994)

• Roy L. Crole, Categories for types, Cambridge University Press (1994) [doi:10.1017/CBO9781139172707]

  (categorical semantics of type theory)

Expositions:

• A. Martini, H. Ehrig, and D. Nunes, Elements of basic category theory, Technical Report 96-5, Technical University Berlin.

• Jaap van Oosten, Basic category theory.

• Paolo Perrone, Notes on Category Theory with examples from basic mathematics. (arXiv)

• Andrea Schalk and H. Simmons, An introduction to category theory in four easy movements, notes for a course offered as part of the MSc. in Mathematical Logic, Manchester University.

• Daniele Turim, Category theory lecture notes, 1996-2001. Based on Mac Lane’s book (1998).

A textbook that introduces categories by examples arising in mathematical physics is

• Robert Geroch, Mathematical Physics, University of Chicago Press (1985) [ISBN:9780226223063]

A textbook with an eye towards the theory of categories of sheaves and their application in homological algebra is

• Kashiwara, Shapira, Categories and Sheaves

The definition of categories in the foundations of homotopy type theory (see at internal category in homotopy type theory) is discussed in

• Benedikt Ahrens, Chris Kapulkin, Michael Shulman, Univalent categories and the Rezk completion, Mathematical Structures in Computer Science 25.5 (2015): 1010-1039 (arXiv:1303.0584)

• Paolo Capriotti, Nicolai Kraus, Univalent Higher Categories via Complete Semi-Segal Types (arXiv:1707.03693)

• Jason Gross, Adam Chlipala, David Spivak, Experience Implementing a Performant Category-Theory Library in Coq (arXiv:1401.7694)

For more references see category theory.