nLab renormalization
Context
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
- Idea
- Details
- In causal perturbation theory
- Epstein-Glaser normalization
- Stückelberg-Petermann renormalization group
- UV-Regularization via Conterterms
- Wilson-Polchinski effective QFT flow
- Renormalization group flow
- Gell-Mann & Low RG flow
- Dimensional regularization
- Connes-Kreimer renormalization
- BPHZ and Hopf-algebraic renormalization
- Lattice renormalization
- Of theories in BV-CS form
- Examples
- Related concepts
- References
Idea
The construction of a perturbative quantum field theory from a given local Lagrangian density (rigorously via causal perturbation theory) involves ambiguities associated with the detailed nature of the quantum processes at point interactions. What is called renormalization is making a choice of fixing these ambiguities to produce a perturbative quantum field theory (Wightman et al. 76).
In causal perturbation theory the renormalization ambiguities are understood as the freedom of extending the time-ordered product of operator-valued distributions to the interaction points, in the sense of extension of distributions. The notorious “infinities that plague quantum field theory” arise only if this extension is not handled correctly and has to be fixed. Hence what historically is called “renormalization” could from a mathematical point of view just be called “normalization” (a point made vividly for instance in Scharf 95, Scharf 01).
The main theorem of perturbative renormalization theory (theorem below) states that any two choices of such (re-)normalizations are uniquely related by a re-definition of the interaction Lagrangian density which introduces further point interactions of higher order (“counter terms”),
The extension of distributions of the time-ordered product may naturally be organized via graphs, the Feynman graphs (Garcia-Bondia & Lazzarini 00, Keller 10, chapter IV), and hence the renormalized perturbative S-matrix defining the perturbative quantum field theory is expressed as a formal power series in renormalized Feynman graphs, the Feynman perturbation series (Keller 10 (IV.12)).
Historically the Feynman perturbation series was motivated from intuition about the would-be path integral, and this is still a popular point of view, despite its lack of rigorous formulation. One may understand the axiomatics on the S-matrix in causal perturbation theory as defining the result of the path integral without actually doing an integration over field configurations.
But while path integral quantization for perturbative quantum field theory remains elusive, it has been shown that the (re-)normalized perturbative quantum field theory thus constructed via causal perturbation theory is, at least under favorable circumstances, equivalently the (Fedosov) formal deformation quantization of the covariant phase space induced by the given interacting Lagrangian density (Collini 16). This identifies the (re-)normalization freedom with the usual freedom in choosing formal deformation quantization.
This also suggest that the construction of the full non-perturbative quantum field theory ought to be given by a strict deformation quantization of the covariant phase space. But presently no example of such for non-trivial interaction in spacetime dimension is known. In particular the phenomenologically interesting case of a complete construction of interacting field theories on 4-dimensional spacetimes is presently unknown. For the case of Yang-Mills theory this open problem is one of the “Millennium Problems” (see at quantization of Yang-Mills theory).
The following is taken from geometry of physics – A first idea of quantum field theory. See there for more backround.
Details
There are different formulations of renormalization:
In causal perturbation theory
We discuss (re-)normalization of relativistic perturbative QFT in the rigorous formulation of causal perturbation theory/perturbative AQFT.
In this rigorous discussion no “infinite divergent quantities” (as in the original informal discussion due to Schwinger-Tomonaga-Feynman-Dyson) that need to be “re-normalized” to finite well-defined quantities are ever considered, instead finite well-defined quantities are considered right away, and the available space of choices is determined. Therefore making such choices is really a normalization of the time-ordered products/Feynman amplitudes (as prominently highlighted in Scharf 95, see title, introduction, and section 4.3). Actual re-normalization is the the change of such normalizations:
-
Normalization
-
Re-Normalization
The construction of perturbative QFTs may be explicitly described by an inductive extension of distributions of time-ordered products/Feynman amplitudes to coinciding interaction points. This type of construction is called
This inductive construction has the advantage that it gives accurate control over the space of available choices of renormalizations (theorem below) but it leaves the nature of the “new interactions” that are to be chosen at coinciding interaction points somwewhat implicit.
Alternatively, one may re-define the interactions explicitly (by adding “counterterms”), depending on a chosen UV cutoff-scale, and construct the limit as the “cutoff is removed”. This is called (“re”-)normalization by
This still leaves open the question how to choose the counterterms. For this it serves to understand the relative effective action induced by the choice of UV cutoff at any given cutoff scale. The infinitesimal change of these relative effective actions follows a universal differential equation, Polchinski's flow equation (prop. below). This makes the problem of (“re”-)normalization be that of solving this differential equation subject to chosen initial data. This is the perspective on (“re”-)normalization called
The main theorem of perturbative renormalization states that different S-matrix schemes are precisely related by vertex redefinitions. This yields the
If a sub-collection of renormalization schemes is parameterized by some group , then the main theorem implies vertex redefinitions depending on pairs of elements of this is known as
Specifically scaling transformations on Minkowski spacetime yields such a collection of renormalization schemes; the corresponding renormalization group flow is known as
Epstein-Glaser normalization
The construction of perturbative quantum field theories around a given gauge fixed relativistic free field vacuum is equivalently, by this prop., the construction of S-matrices in the sense of causal perturbation theory (this def.) for the given local interaction . By prop. the construction of these S-matrices is inductively in a choice of extension of distributions (remark and def. below) of the corresponding -ary time-ordered products of the interaction to the locus of coinciding interaction points (the fat diagonal). An inductive construction of the S-matrix this way is called Epstein-Glaser-("re"-)normalization (this def.).
By paying attention to the scaling degree (def. below) one may precisely characterize the space of choices in the extension of distributions (prop. below): For a given local interaction it is inductively in a finite-dimensional affine space. This conclusion is theorem below.
Proposition
(("re"-)normalization is inductive extension of time-ordered products to diagonal)
Let be a gauge-fixed relativistic free vacuum according to this def..
Assume that for , time-ordered products of arity have been constructed in the sense of this def.. Then the time-ordered product of arity is uniquely fixed on the complement
of the image of the diagonal inclusion (where we regarded as a generalized function on according to this remark).
This statement appears in (Popineau-Stora 82), with (unpublished) details in (Stora 93), following personal communication by Henri Epstein (according to Dütsch 18, footnote 57). Following this, statement and detailed proof appeared in (Brunetti-Fredenhagen 00).
Proof
We will construct an open cover of by subsets which are disjoint unions of non-empty sets that are in causal order, so that by causal factorization the time-ordered products on these subsets are uniquely given by . Then we show that these unique products on these special subsets do coincide on intersections. This yields the claim by a partition of unity.
We now say this in detail:
For write . For , define the subset
Since the causal order-relation involves the closed future cones/closed past cones, respectively, it is clear that these are open subsets. Moreover it is immediate that they form an open cover of the complement of the diagonal:
(Because any two distinct points in the globally hyperbolic spacetime may be causally separated by a Cauchy surface, and any such may be deformed a little such as not to intersect any of a given finite set of points. )
Hence the condition of causal factorization on implies that restricted to any these have to be given (in the condensed generalized function-notation from this remark) on any unordered tuple with corresponding induced tuples and by
This shows that is unique on if it exists at all, hence if these local identifications glue to a global definition of . To see that this is the case, we have to consider any two such subsets
By definition this implies that for
a tuple of spacetime points which decomposes into causal order with respect to both these subsets, the corresponding mixed intersections of tuples are spacelike separated:
By the assumption that the satisfy causal factorization, this implies that the corresponding time-ordered products commute:
Using this we find that the identifications of on and on , accrding to (1), agree on the intersection: in that for we have
Here in the first step we expanded out the two factors using (1) for , then under the brace we used (2) and in the last step we used again (1), but now for .
To conclude, let
be a partition of unity subordinate to the open cover formed by the :
Then the above implies that setting for any
is well defined and satisfies causal factorization.
Remark
(time-ordered products of fixed interaction as distributions)
Let be a gauge-fixed relativistic free vacuum according to this def., and assume that the field bundle is a trivial vector bundle (this example)
and let
be a polynomial local observable, to be regarded as a adiabatically switched interaction action functional. This means that there is a finite set
of Lagrangian densities which are monomials in the field and jet coordinates, and a corresponding finite set
of adiabatic switchings, such that
is the transgression of variational differential forms (this def.) of the sum of the products of these adiabatic switching with these Lagrangian densities.
In order to discuss the S-matrix and hence the time-ordered products of the special form it is sufficient to restrict attention to the restriction of each to the subspace of local observables induced by the finite set of Lagrangian densities .
This restriction is a continuous linear functional on the corresponding space of bump functions , hence a dstributional section of a corresponding trivial vector bundle.
In terms of this, prop. says that the choice of time-ordered products is inductively in a choice of extension of distributions to the diagonal.
If is Minkowski spacetime and we impose the renormalization condition “translation invariance” (this def.) then each is a distribution on and the extension of distributions is from the complement of the origina .
Therefore we now discuss extension of distributions (def. below) on Cartesian spaces from the complement of the origin to the origin. Since the space of choices of such extensions turns out to depend on the scaling degree of distributions, we first discuss that (def. below).
Definition
Let . For a positive real number write
for the diffeomorphism given by multiplication with , using the canonical real vector space-structure of .
Then for a distribution on the Cartesian space the rescaled distribution is the pullback of along
Explicitly, this is given by
Similarly for an open subset which is invariant under , the rescaling of a distribution is is .
Definition
(scaling degree of a distribution)
Let and let be an open subset of Cartesian space which is invariant under rescaling (def. ) for all , and let be a distribution on this subset. Then
-
The scaling degree of is the infimum
of the set of real numbers such that the limit of the rescaled distribution (def. ) vanishes. If there is no such one sets .
-
The degree of divergence of is the difference of the scaling degree by the dimension of the underlying space:
Example
(scaling degree of non-singular distributions)
If is a non-singular distribution given by bump function , then its scaling degree (def. ) is non-positive
Specifically if the first non-vanishing partial derivative of at 0 occurs at order , then the scaling degree of is .
Proof
By definition we have for any bump function that
where in last line we applied change of integration variables.
The limit of this expression is clearly zero for all , which shows the first claim.
If moreover the first non-vanishing partial derivative of occurs at order , then Hadamard's lemma says that is of the form
where the are smooth functions. Hence in this case
This makes manifest that the expression goes to zero with precisely for , which means that
in this case.
Example
(scaling degree of derivatives of delta-distributions)
Let be a multi-index and the corresponding partial derivatives of the delta distribution supported at . Then the degree of divergence (def. ) of is the total order the derivatives
where .
Proof
By definition we have for any bump function that
where in the last step we used the chain rule of differentiation. It is clear that this goes to zero with as long as . Hence .
Example
(scaling degree of Feynman propagator on Minkowski spacetime)
Let
be the Feynman propagator for the massive free real scalar field on -dimensional Minkowski spacetime (this prop.). Its scaling degree is
(Brunetti-Fredenhagen 00, example 3 on p. 22)
Proof
Regarding as a generalized function via the given Fourier-transform expression, we find by change of integration variables in the Fourier integral that in the scaling limit the Feynman propagator becomes that for vannishing mass, which scales homogeneously:
Proposition
(basic properties of scaling degree of distributions)
Let and be a distribution as in def. , such that its scaling degree is finite: (def. ). Then
-
For , the partial derivative of distributions increases scaling degree at most by :
-
For , the product of distributions with the smooth coordinate functions decreases scaling degree at least by :
-
Under tensor product of distributions their scaling degrees add:
for another distribution on ;
-
for and for ;
(Brunetti-Fredenhagen 00, lemma 5.1, Dütsch 18, exercise 3.34)
Proof
The first three statements follow with manipulations as in example and example .
For the fourth…
Proposition
(scaling degree of product distribution)
Let be two distributions such that
-
both have finite degree of divergence (def. )
-
their product of distributions is well-defined
(in that their wave front sets satisfy Hörmander's criterion)
then the product distribution has degree of divergence bounded by the sum of the separate degrees:
With the concept of scaling degree of distributions in hand, we may now discuss extension of distributions:
Definition
Let be an inclusion of open subsets of some Cartesian space. This induces the operation of restriction of distributions
Given a distribution , then an extension of to is a distribution such that
Proposition
(unique extension of distributions with negative degree of divergence)
For , let be a distribution on the complement of the origin, with negative degree of divergence at the origin
Then has a unique extension of distributions to the origin with the same degree of divergence
(Brunetti-Fredenhagen 00, theorem 5.2, Dütsch 18, theorem 3.35 a))
Proof
Regarding uniqueness:
Suppose and are two extensions of with . Both being extensions of a distribution defined on , this difference has support at the origin . By this prop. this implies that it is a linear combination of derivatives of the delta distribution supported at the origin:
for constants . But by this example the degree of divergence of these point-supported distributions is non-negative
This implies that for all , hence that the two extensions coincide.
Regarding existence:
Let
be a bump function which is and constant on 1 over a neighbourhood of the origin. Write
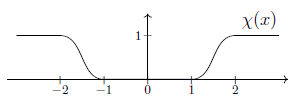
graphics grabbed from Dütsch 18, p. 108
and for a positive real number, write
Since the product has support of a distribution on a complement of a neighbourhood of the origin, we may extend it by zero to a distribution on all of , which we will denote by the same symbols:
By construction coincides with away from a neighbourhood of the origin, which moreover becomes arbitrarily small as increases. This means that if the following limit exists
then it is an extension of .
To see that the limit exists, it is sufficient to observe that we have a Cauchy sequence, hence that for all the difference
becomes arbitrarily small.
It remains to see that the unique extension thus established has the same scaling degree as . This is shown in (Brunetti-Fredenhagen 00, p. 24).
Proposition
(space of point-extensions of distributions)
For , let be a distribution of degree of divergence .
Then does admit at least one extension (def. ) to a distribution , and every choice of extension has the same degree of divergence as
Moreover, any two such extensions and differ by a linear combination of partial derivatives of distributions of order of the delta distribution supported at the origin:
for a finite number of constants .
This is essentially (Hörmander 90, thm. 3.2.4). We follow (Brunetti-Fredenhagen 00, theorem 5.3), which was inspired by (Epstein-Glaser 73, section 5). Review of this approach is in (Dütsch 18, theorem 3.35 (b)), see also remark below.
Proof
For a smooth function, and , we say that vanishes to order at the origin if all partial derivatives with multi-index of total order vanish at the origin:
By Hadamard's lemma, such a function may be written in the form
for smooth functions .
Write
for the subspace of that of all bump functions on those that vanish to order at the origin.
By definition this is equivalently the joint kernel of the partial derivatives of distributions of order of the delta distribution supported at the origin:
Therefore every continuous linear projection
may be obtained from a choice of dual basis to the , hence a choice of smooth functions
such that
by setting
hence
Together with Hadamard's lemma in the form (5) this means that every is decomposed as
Now let
Observe that (by this prop.) the degree of divergence of the product of distributions with is negative
Therefore prop. says that each for has a unique extension to the origin. Accordingly the composition has a unique extension, by (8):
That says that is of the form
for a finite number of constants .
Notice that for any extension the exact value of the here depends on the arbitrary choice of dual basis used for this construction. But the uniqueness of the first summand means that for any two choices of extensions and , their difference is of the form
where the constants are independent of any choices.
It remains to see that all these in fact have the same degree of divergence as .
By this example the degree of divergence of the point-supported distributions on the right is .
Therefore to conclude it is now sufficient to show that
This is shown in (Brunetti-Fredenhagen 00, p. 25).
Remark
(“W-extensions”)
Since in Brunetti-Fredenhagen 00, (38) the projectors (7) are denoted “”, the construction of extensions of distributions via the proof of prop. has come to be called “W-extensions” (e.g Dütsch 18).
In conclusion we obtain the central theorem of causal perturbation theory:
Theorem
(existence and choices of ("re"-)normalization of S-matrices/perturbative QFTs)
Let be a gauge-fixed relativistic free vacuum, according to this def., such that the underlying spacetime is Minkowski spacetime and the Wightman propagator is translation-invariant.
Then:
-
an S-matrix scheme (this def.) around this vacuum exists;
-
for a local observable, regarded as an adiabatically switched interaction action functional, the space of possible choices of S-matrices
hence of the corresponding perturbative QFTs, by this prop., is, inductively in , a finite dimensional affine space, parameterizing the extension of the time-ordered product to the locus of coinciding interaction points (the fat diagonal).
Proof
By prop. the Feynman propagator is finite scaling degree of a distribution, so that by prop. the binary time-ordered product away from the diagonal has finite scaling degree.
By prop. this implies that in the inductive description of the time-ordered products by prop. , each induction step is the extension of distributions of finite scaling degree of a distribution to the point. By prop. this always exists.
This proves the first statement.
Now if a polynomial local interaction is fixed, then via remark each induction step involved extending a finite number of distributions, each of finite scaling degree. By prop. the corresponding space of choices is in each step a finite-dimensional affine space.
Stückelberg-Petermann renormalization group
A genuine re-normalization is the passage from one S-matrix ("re"-)normalization scheme to another such scheme . The inductive Epstein-Glaser ("re"-normalization) construction (prop. ) shows that the difference between any and is inductively in a choice of extra term in the time-ordered product of factors, equivalently in the Feynman amplitudes for Feynman diagrams with vertices, that contributes when all of these vertices coincide in spacetime (prop. ).
A natural question is whether these additional interactions that appear when several interaction vertices coincide may be absorbed into a re-definition of the original interaction . Such an interaction vertex redefinition (def. below)
should perturbatively send local interactions to local interactions with higher order corrections.
The main theorem of perturbative renormalization (theorem below) says that indeed under mild conditions every re-normalization is induced by such an interaction vertex redefinition in that there exists a unique such redefinition so that for every local interaction we have that scattering amplitudes for the interaction computed with the ("re"-)normalization scheme equal those computed with but applied to the re-defined interaction :
This means that the interaction vertex redefinitions form a group under composition which acts transitively and freely, hence regularly, on the set of S-matrix ("re"-)normalization schemes; this is called the Stückelberg-Petermann renormalization group (theorem below).
Definition
(perturbative interaction vertex redefinition)
Let be a gauge fixed free field vacuum (this def.).
A perturbative interaction vertex redefinition (or just vertex redefinition, for short) is an endofunction
on local observables with formal parameters adjoined (this def.) such that there exists a sequence of continuous linear functionals, symmetric in their arguments, of the form
such that for all the following conditions hold:
-
(perturbation)
-
and
-
(field independence) The local observable depends on the field histories only through its argument , hence by the chain rule:
(10)
The following proposition should be compared to the axiom of causal additivity of the S-matrix scheme (this equation):
Proposition
(local additivity of vertex redefinitions)
Let be a gauge fixed free field vacuum (this def.) and let be a vertex redefinition (def. ).
Then for all local observables with spacetime support denoted (this def.) we have
-
(local additivity)
-
(preservation of spacetime support)
hence in particular
Proof
Under the inclusion
of local observables into polynomial observables we may think of each as a generalized function, as for time-ordered products in this remark.
Hence if
is the transgression of a Lagrangian density we get
Now by definition is in the subspace of local observables, i.e. those polynomial observables whose coefficient distributions are supported on the diagonal, which means that
Together with the axiom “field independence” (10) this means that the support of these generalized functions in the integrand here must be on the diagonal, where .
By the assumption that the spacetime supports of and are disjoint, this means that only the summands with and those with contribute to the above sum. Removing the overcounting of those summands where all we get
This directly implies the claim.
As a corollary we obtain:
Proposition
(composition of S-matrix scheme with vertex redefinition is again S-matrix scheme)
Let be a gauge fixed free field vacuum (this def.) and let be a vertex redefinition (def. ).
Then for
and S-matrix scheme (this def.), the composite
is again an S-matrix scheme.
Moreover, if satisfies the renormalization condition “field independence” (this prop.), then so does .
(e.g Dütsch 18, theorem 3.99 (b))
Proof
It is clear that causal order of the spacetime supports implies that they are in particular disjoint
Therefore the local additivity of (prop. ) and the causal factorization of the S-matrix (this remark) imply the causal factorization of the composite:
But by this prop. this implies in turn causal additivity and hence that is itself an S-matrix scheme.
Finally that satisfies “field indepndence” if does is immediate by the chain rule, given that satisfies this condition by definition.
Proposition
(any two S-matrix renormalization schemes differ by unique vertex redefinition)
Let be a gauge fixed free field vacuum (this def.).
Then for any two S-matrix schemes (this def.) which both satisfy the renormalization condition “field independence”, the there exists a unique vertex redefinition (def. ) relating them by composition, i. e. such that
Proof
By applying both sides of the equation to linear combinations of local observables of the form and then taking derivatives with respect to at (as in this example) we get that the equation in question implies
which in components means that
where are the time-ordered products corresponding to (by this example) and those correspondong to .
Here the sum on the right runs over all ways that in the composite a -ary operation arises as the composite of an -ary time-ordered product applied to the -ary components of , for running from 1 to ; except for the case , which is displayed separately in the second line
This shows that if exists, then it is unique, because its coefficients are inductively in given by the expressions
(The symbol under the brace is introduced as a convenient shorthand for the term above the brace.)
Hence it remains to see that the defined this way satisfy the conditions in def. .
The condition “perturbation” is immediate from the corresponding condition on and .
Similarly the condition “field independence” follows immediately from the assumoption that and satisfy this condition.
It only remains to see that indeed takes values in local observables. Given that the time-ordered products a priori take values in the larrger space of microcausal polynomial observables this means to show that the spacetime support of is on the diagonal.
But observe that, as indicated in the above formula, the term over the brace may be understood as the coefficient at order of the exponential series-expansion of the composite , where
is the truncation of the vertex redefinition to degree . This truncation is clearly itself still a vertex redefinition (according to def. ) so that the composite is still an S-matrix scheme (by prop. ) so that the are time-ordered products (by this example).
So as we solve inductively in degree , then for the induction step in degree the expressions and agree and are both time-ordered products. By this prop. this implies that and agree away from the diagonal. This means that their difference is supported on the diagonal, and hence is indeed local.
In conclusion this establishes the following pivotal statement of perturbative quantum field theory:
Theorem
(main theorem of perturbative renormalization – Stückelberg-Petermann renormalization group of vertex redefinitions)
Let be a gauge fixed free field vacuum (this def.).
-
the vertex redefinitions (def. ) form a group under composition;
-
the set of S-matrix ("re"-)normalization schemes (this def., this remark) satisfying the renormalization condition “field independence” (this prop.) is a torsor over this group, hence equipped with a regular action in that
-
the set of S-matrix schemes is non-empty;
-
any two S-matrix ("re"-)normalization schemes , are related by a unique vertex redefinition via composition:
-
This group is called the Stückelberg-Petermann renormalization group.
Typically one imposes a set of renormalization conditions (this def.) and considers the corresponding subgroup of vertex redefinitions preserving these conditions.
Proof
The group-structure and regular action is given by prop. and prop. . The existence of S-matrices follows is the statement of Epstein-Glaser ("re"-)normalization in theorem .
UV-Regularization via Conterterms
While Epstein-Glaser renormalization (prop. ) gives a transparent picture on the space of choices in ("re"-)normalization (theorem ) the physical nature of the higher interactions that it introduces at coincident interaction points (via the extensions of distributions in prop. ) remains more implicit. But the main theorem of perturbative renormalization (theorem ), which re-expresses the difference between any two such choices as an interaction vertex redefinition, suggests that already the choice of ("re"-)normalization itself should have an incarnation in terms of interaction vertex redefinitions.
This may be realized via a construction of ("re"-)normalization in terms of UV-regularization (prop. below): For any choice of “UV-cutoff”, given by an approximation of the Feynman propagator by non-singular distributions (def. below) there is a unique “effective S-matrix” induced at each cutoff scale (def. below). While the “UV-limit” does not in general exist, it may be “regularized” by applying suitable interaction vertex redefinitions ; if the higher-order corrections that these introduce serve to “counter” (remark below) the coresponding UV-divergences.
This perspective of ("re"-)normalization via via counterterms is often regarded as the primary one. Its elegant proof in prop. below, however relies on the Epstein-Glaser renormalization via inductive extensions of distributions and uses the same kind of argument as in the proof of the main theorem of perturbative renormalization (theorem ) that establishes the Stückelberg-Petermann renormalization group.
Definition
Let be a gauge fixed relativistic free vacuum over Minkowski spacetime (according to this def.), where is the corresponding Wightman propagator inducing the Feynman propagator
by .
Then a choice of UV cutoffs for perturbative QFT around this vacuum is a collection of non-singular distributions parameterized by positive real numbers
such that:
-
each satisfies the following basic properties
-
(translation invariance)
-
(symmetry)
i.e.
-
-
the interpolate between zero and the Feynman propagator, in that, in the Hörmander topology:
-
the limit as exists and is zero
-
the limit as exists and is the Feynman propagator:
-
example: relativistic momentum cutoff with -regularization (Keller-Kopper-Schophaus 97, section 6.1, Dütsch 18, example 3.126)
Definition
Let be a gauge fixed relativistic free vacuum (according to this def.) and let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ).
We say that the effective S-matrix scheme at cutoff scale
is the exponential series
with respect to the star product induced by the (this def.).
This is evidently defined on all polynomial observables as shown, and restricts to an endomorphism on microcausal polynomial observables as shown, since the contraction coefficients are non-singular distributions, by definition of UV cutoff.
Proposition
(("re"-)normalization via UV regularization)
Let be a gauge fixed relativistic free vacuum (according to this def.) and let a polynomial local observable, regarded as an adiabatically switched interaction action functional.
Let moreover be a UV cutoff (def. ); with the induced effective S-matrix schemes (12).
Then
-
there exists a -parameterized interaction vertex redefinition (this def.) such that the limit of effective S-matrix schemes (12) applied to the -redefined interactions
exists and is a genuine S-matrix scheme around the given vacuum (this def.);
-
every S-matrix scheme around the given vacuum arises this way.
These are called counterterms (remark below) and the composite is called a UV regularization of the effective S-matrices .
Hence UV-regularization via counterterms is a method of ("re"-)normalization of perturbative QFT (this def.).
This was claimed in (Brunetti-Dütsch-Fredenhagen 09, (75)), a proof was indicated in (Dütsch-Fredenhagen-Keller-Rejzner 14, theorem A.1).
Proof
Let be a sequence of projection maps as in (6) defining an Epstein-Glaser ("re"-)normalization (prop. ) of time-ordered products as extensions of distributions of the , regarded as distributions via remark , by the choice in (9).
We will construct that in terms of these projections .
First consider some convenient shorthand:
For , write . Moreover, for write for the -ary coefficient in the expansion of the composite , as in equation (11) in the proof of the main theorem of perturbative renormalization (theorem ).
In this notation we need to find such that for each we have
We proceed by induction over .
Since by definition , and , the statement is trivially true for and .
So assume now and has been found such that (13) holds.
Observe that with the chosen renormalizing projection the time-ordered product may be expressed as follows:
Here in the first step we inserted the causal decomposition (4) of in terms of the away from the diagonal, as in the proof of prop. , which is admissible because the image of vanishes on the diagonal. In the second step we replaced the star-product of the Feynman propagator with the limit over the star-products of the regularized propagators , which converges by the nature of the Hörmander topology (which is assumed by def. ).
Hence it is sufficient to find and such that
subject to these two conditions:
-
is local;
-
.
Now by expanding out the left hand side of (15) as
(which uses the condition ) we find the unique solution of (15) for , in terms of the and (the latter still to be chosen) to be:
We claim that the following choice works:
To prove this, we need to show that 1) the resulting is local and 2) the limit of vanishes as .
First regarding the locality of : By inserting (17) into (16) we obtain
By definition is the identity on test functions (adiabatic switchings) that vanish at the diagonal. This means that is supported on the diagonal, and is hence local.
Second we need to show that :
By applying the analogous causal decomposition (4) to the regularized products, we find
Using this we compute as follows:
Here in the first step we inserted (18); in the second step we used that in the Hörmander topology the product of distributions preserves limits in each variable and in the third step we used the induction assumption (13) and the definition of UV cutoff (def. ).
Inserting this for the first summand in (17) shows that .
In conclusion this shows that a consistent choice of counterterms exists to produce some S-matrix .
It just remains to see that for every other S-matrix there exist counterterms such that .
But by the main theorem of perturbative renormalization (theorem ) we know that there exists a vertex redefinition such that
and hence with counterterms for given, then counterterms for any are given by the composite .
Remark
Let be a gauge fixed relativistic free vacuum (according to this def.) and let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ).
Consider
a local observable, regarded as an adiabatically switched interaction action functional.
Then prop. says that there exist vertex redefinitions of this interaction
parameterized by , such that the limit
exists and is an S-matrix for perturbative QFT with the given interaction .
In this case the difference
(which by the axiom “perturbation” in this def. is at least of second order in the coupling constant/source field, as shown) is called a choice of counterterms at cutoff scale . These are new interactions which are added to the given interaction at cutoff scale
In this language prop. says that for every free field vacuum and every choice of local interaction, there is a choice of counterterms to the interaction that defines a corresponding ("re"-)normalized perturbative QFT, and every (re"-)normalized perturbative QFT arises from some choice of counterterms.
Wilson-Polchinski effective QFT flow
We have seen above that a choice of UV cutoff induces effective S-matrix schemes at cutoff scale (def. ). To these one may associated non-local relative effective actions (def. below) which are such that their effective scattering amplitudes at scale coincide with the true scattering amplitudes of a genuine local interaction as the cutoff is removed. This is the Wilsonian picture of effective quantum field theory at a given cutoff scale (remark below). Crucially the “flow” of the relative effective actions with the cutoff scale satisfies a differential equation that in itself is independent of the full UV-theory; this is Polchinski's flow equation (prop. below). Solving this equation for given choice of initial value data is hence another way of choosing ("re"-)normalization constants.
Proposition
(effective S-matrix schemes are invertible functions)
Let be a gauge fixed relativistic free vacuum (according to this def.) and let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ).
Write
for the subspace of the space of formal power series in with coefficients polynomial observables on those which are at least of first order in , i.e. those that vanish for (as in this def.).
Write moreover
for the subspace of polynomial observables which are the sum of 1 (the multiplicative unit) with an observable at least linear n .
Then the effective S-matrix schemes (def. ) restrict to linear isomorphisms of the form
Proof
Since each is symmetric (def. ) if follows by general properties of star products (this prop.) just as for the genuine time-ordered product on regular polynomial observables (this prop.) that eeach the “effective time-ordered product” is isomorphic to the pointwise product (this def.)
for
(as in this equation).
In particular this means that the effective S-matrix arises from the exponential series for the pointwise product by conjugation with :
(just as for the genuine S-matrix on regular polynomial observables in this def.).
Now the exponential of the pointwise product on has as inverse function the natural logarithm power series, and since evidently preserves powers of this conjugates to an inverse at each UV cutoff scale :
Definition
Let be a gauge fixed relativistic free vacuum (according to this def.) and let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ).
Consider
a local observable regarded as an adiabatically switched interaction action functional.
Then for
two UV cutoff-scale parameters, we say the relative effective action is the image of this interaction under the composite of the effective S-matrix scheme at scale (12) and the inverse function of the effective S-matrix scheme at scale (via prop. ):
For chosen counterterms (remark ) hence for chosen UV regularization (prop. ) this makes sense also for and we write:
Remark
(effective quantum field theory)
Let be a gauge fixed relativistic free vacuum (according to this def.), let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ), and let be a corresponding UV regularization (prop. ).
Consider a local observable
regarded as an adiabatically switched interaction action functional.
Then def. and def. say that for any the effective S-matrix (12) of the relative effective action (21) equals the genuine S-matrix of the genuine interaction :
In other words the relative effective action encodes what the actual perturbative QFT defined by effectively looks like at UV cutoff .
Therefore one says that defines effective quantum field theory at UV cutoff .
Notice that in general is not a local interaction anymore: By prop. the image of the inverse of the effective S-matrix is microcausal polynomial observables in and there is no guarantee that this lands in the subspace of local observables.
Therefore effective quantum field theories at finite UV cutoff-scale are in general not local field theories, even if their limit as is, via prop. .
Proposition
(effective action is relative effective action at )
Let be a gauge fixed relativistic free vacuum (according to this def.) and let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ).
Then the relative effective action (def. ) at is the actual effective action (this def.) in the sense of the the Feynman perturbation series of Feynman amplitudes (this def.) for connected Feynman diagrams :
More generally this holds true for any
where denotes the evident version of the Feynman amplitude (this def.) with time-ordered products replaced by effective time ordered product at scale as in (def. ).
Proof
Observe that the effective S-matrix scheme at scale (12) is the exponential series with respect to the pointwise product (this def.)
Therefore the statement to be proven says equivalently that the exponential series of the effective action with respect to the pointwise product is the S-matrix:
That this is the case is the statement of this prop..
The definition of the relative effective action in def. invokes a choice of UV regularization (prop. ). While (by that proposition and the main theorem of perturbative renormalization (theorem ) this is guaranteed to exist, in practice one is after methods for constructing this without specifying it a priori.
But the collection relative effective actions for “flows” with the cutoff-parameters and in particular also with (remark below) which suggests that examination of this flow yields information about full theory at .
This is made precise by Polchinski's flow equation (prop. below), which is the infinitesimal version of the “Wilsonian RG flow” (remark ). As a differential equation it is independent of the choice of and hence may be used to solve for the Wilsonian RG flow without knowing in advance.
The freedom in choosing the initial values of this differential equation corresponds to the ("re"-)normalization freedom in choosing the UV regularization . In this sense “Wilsonian RG flow” is a method of ("re"-)normalization of perturbative QFT (this def.).
Remark
(Wilsonian groupoid of effective quantum field theories)
Let be a gauge fixed relativistic free vacuum (according to this def.) and let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ).
Then the relative effective actions (def. ) satisfy
This is similar to a group of UV-cutoff scale-transformations. But since the composition operations are only sensible when the UV-cutoff labels match, as shown, it is really a groupoid action.
This is often called the Wilsonian RG.
We now consider the infinitesimal version of this “flow”:
Proposition
Let be a gauge fixed relativistic free vacuum (according to this def.), let be a choice of UV cutoffs for perturbative QFT around this vacuum (def. ), such that is differentiable.
Then for every choice of UV regularization (prop. ) the corresponding relative effective actions (def. ) satisfy the following differential equation:
where on the right we have the star product induced by (this def.).
This goes back to (Polchinski 84, (27)). The rigorous formulation and proof is due to (Brunetti-Dütsch-Fredenhagen 09, prop. 5.2, Dütsch 10, theorem 2).
Proof
First observe that for any polynomial observable we have
Here denotes the functional derivative of the th tensor factor of , and the binomial coefficient counts the number of ways that an unordered pair of distinct labels of tensor factors may be chosen from a total of tensor factors, where we use that the star product is commutative (by symmetry of ) and associative (by this prop.).
With this and the defining equality (22) we compute as follows:
Acting on this equation with the multiplicative inverse (using that is a commutative product, so that exponentials behave as usual) this yields the claimed equation.
Renormalization group flow
In perturbative quantum field theory the construction of the scattering matrix , hence of the interacting field algebra of observables for a given interaction perturbing around a given free field vacuum, involves choices of normalization of time-ordered products/Feynman diagrams (traditionally called "re"-normalizations) encoding new interactions that appear where several of the original interaction vertices defined by coincide.
Whenever a group acts on the space of observables of the theory such that conjugation by this action takes ("re"-)normalization schemes into each other, then these choices of ("re"-)normalization are parameterized by – or “flow with” – the elements of . This is called renormalization group flow (prop. below); often called RG flow, for short.
The archetypical example here is the group of scaling transformations on Minkowski spacetime (def. below), which induces a renormalization group flow (prop. below) due to the particular nature of the Wightman propagator resp. Feynman propagator on Minkowski spacetime (example below). In this case the choice of ("re"-)normalization hence “flows with scale”.
Now the main theorem of perturbative renormalization states that (if only the basic renormalization condition called “field independence” is satisfied) any two choices of ("re"-)normalization schemes and are related by a unique interaction vertex redefinition , as
Applied to a parameterization/flow of renormalization choices by a group this hence induces an interaction vertex redefinition as a function of . One may think of the shape of the interaction vertices as fixed and only their (adiabatically switched) coupling constants as changing under such an interaction vertex redefinition, and hence then one has coupling constants that are parameterized by elements of :
This dependendence is called running of the coupling constants under the renormalization group flow (def. below).
One example of renormalization group flow is that induced by scaling transformations (prop. below). This is the original and main example of the concept (Gell-Mann & Low 54)
In this case the running of the coupling constants may be understood as expressing how “more” interactions (at higher energy/shorter wavelength) become visible (say to experiment) as the scale resolution is increased. In this case the dependence of the coupling on the parameter happens to be differentiable; its logarithmic derivative (denoted “” in Gell-Mann & Low 54) is known as the beta function (Callan 70, Symanzik 70):
The running of the coupling constants is not quite a representation of the renormalization group flow, but it is a “twisted” representation, namely a group 1-cocycle (prop. below). For the case of scaling transformations this may be called the Gell-Mann-Low renormalization cocycle (Brunetti-Dütsch-Fredenhagen 09).
Proposition
Let
be a relativistic free vacuum (according to this def.) around which we consider interacting perturbative QFT.
Consider a group equipped with an action on the Wick algebra of off-shell microcausal polynomial observables with formal parameters adjoined (as in this def.)
hence for each a continuous linear map which has an inverse and is a homomorphism of the Wick algebra-product (the star product induced by the Wightman propagator of the given vauum )
such that the following conditions hold:
-
the action preserves the subspace of off-shell polynomial local observables, hence it restricts as
-
the action respects the causal order of the spacetime support (this def.) of local observables, in that for we have
for all .
Then:
The operation of conjugation by this action on observables induces an action on the set of S-matrix renormalization schemes (this def., this remark), in that for
a perturbative S-matrix scheme around the given free field vacuum , also the composite
is an S-matrix scheme, for all .
More generally, let
be a collection of gauge fixed free field vacua parameterized by elements , all with the same underlying field bundle; and consider as above, except that it is not an automorphism of any Wick algebra, but an isomorphism between the Wick algebra-structures on various vacua, in that
for all
Then if
is a collection of S-matrix schemes, one around each of the gauge fixed free field vacua , it follows that for all pairs of group elements the composite
is an S-matrix scheme around the vacuum labeled by .
Since therefore each element in the group picks a different choice of normalization of the S-matrix scheme around a given vacuum at , we call the assignment a re-normalization group flow.
(Brunetti-Dütsch-Fredenhagen 09, sections 4.2, 5.1, Dütsch 18, section 3.5.3)
Proof
It is clear from the definition that each satisfies the axiom “perturbation” (in this def.).
In order to verify the axiom “causal additivity”, observe, for convenience, that by this prop. it is sufficient to check causal factorization.
So consider two local observables whose spacetime support is in causal order.
We need to show that the
for all .
Using the defining properties of and the causal factorization of we directly compute as follows:
Definition
Let
be a relativistic free vacuum (according to this def.) around which we consider interacting perturbative QFT, let be an S-matrix scheme around this vacuum and let be a renormalization group flow according to prop. , such that each re-normalized S-matrix scheme satisfies the renormalization condition “field independence”.
Then by the main theorem of perturbative renormalization (this prop.) there is for every pair a unique interaction vertex redefinition
which relates the corresponding two S-matrix schemes via
If one thinks of an interaction vertex, hence a local observable , as specified by the (adiabatically switched) coupling constants multiplying the corresponding interaction Lagrangian densities as
(where denotes transgression of variational differential forms) then exhibits a dependency of the (adiabatically switched) coupling constants of the renormalization group flow parameterized by . The corresponding functions
are then called running coupling constants.
(Brunetti-Dütsch-Fredenhagen 09, sections 4.2, 5.1, Dütsch 18, section 3.5.3)
Proposition
(running coupling constants are group cocycle over renormalization group flow)
Consider running coupling constants
as in def. . Then for all the following equality is satisfied by the “running functions” (25):
(Brunetti-Dütsch-Fredenhagen 09 (69), Dütsch 18, (3.325))
Proof
Directly using the definitions, we compute as follows:
This demonstrates the equation between vertex redefinitions to be shown after composition with an S-matrix scheme. But by the uniqueness-clause in the main theorem of perturbative renormalization (theorem ) the composition operation as a function from vertex redefinitions to S-matrix schemes is injective. This implies the equation itself.
Gell-Mann & Low RG flow
We discuss (prop. below) that, if the field species involved have well-defined mass dimension (example below) then scaling transformations on Minkowski spacetime (example below) induce a renormalization group flow (def. ). This is the original and main example of renormalization group flows (Gell-Mann& Low 54).
Example
(scaling transformations and mass dimension)
Let
be a field bundle which is a trivial vector bundle over Minkowski spacetime .
For a positive real number, write
for the operation of multiplication by using the real vector space-structure of the Cartesian space underlying Minkowski spacetime.
By pullback this acts on field histories (sections of the field bundle) via
Let then
be a 1-parameter collection of relativistic free vacua on that field bundle, according to this def., and consider a decomposition into a set of field species (this def.) such that for each the collection of Feynman propagators for that species scales homogeneously in that there exists
such that for all we have (using generalized functions-notation)
Typically rescales a mass parameter, in which case is also called the mass dimension of the field species .
Let finally
be the function on off-shell polynomial observables given on field observables by pullback along followed by multiplication by taken to the negative power of the mass dimension, and extended from there to all polynomial observables as an algebra homomorphism.
This constitutes an action of the group
of positive real numbers (under multiplication) on polynomial observables, called the group of scaling transformations for the given choice of field species and mass parameters.
Example
(mass dimension of scalar field)
Consider the Feynman propagator of the free real scalar field on Minkowski spacetime for mass parameter ; a Green function for the Klein-Gordon equation.
Let the group of scaling transformations on Minkowski spacetime (def. ) act on the mass parameter by inverse multiplication
Then we have
and hence the corresponding mass dimension (def. ) of the real scalar field on is
Proof
By (this prop.) the Feynman propagator in question is given by the Cauchy principal value-formula (in generalized function-notation)
By applying change of integration variables in the Fourier transform this becomes
Proposition
(scaling transformations are renormalization group flow)
Let
be a relativistic free vacua on that field bundle, according to this def. equipped with a decomposition into a set of field species (this def.) such that for each the collection of Feynman propagators the corresponding field species has a well-defined mass dimension (def. )
Then the action of the group of scaling transformations (def. ) is a renormalization group flow in the sense of this prop..
Proof
It is clear that rescaling preserves causal order and the renormalization condition of “field indepencen”.
The condition we need to check is that for two microcausal polynomial observables we have for any that
By the assumption of decomposition into free field species , it is sufficient to check this for each species . Moreover, by the nature of the star product on polynomial observables, which is given by iterated contractions with the Wightman propagator, it is sufficient to check this for one such contraction.
Observe that the scaling behaviour of the Wightman propagator is the same as the behaviour (26) of the correspponding Feynman propagator. With this we directly compute as follows:
Dimensional regularization
Discussion of renormalization via dimensional regularization in the rigorous context of causal perturbation theory is due to Dütsch-Fredenhagen-Keller-Rejzner 14, section 4.
Connes-Kreimer renormalization
Discussion of the Connes-Kreimer Hopf algebraic renormalization in causal perturbation theory is in Dütsch-Fredenhagen-Keller-Rejzner 14, section 5.
(…)
BPHZ and Hopf-algebraic renormalization
The phenomenon
In the study of perturbative quantum field theory one is concerned with functions – called amplitudes – that take a collection of graphs – called Feynman graphs – to Laurent polynomials in a complex variable – called the (dimensional) regularization parameter –
and wishes to extract a “meaningful” finite component when evaluated at vanishing regularization parameter .
A prescription – called renormalization scheme – for adding to a given amplitude in a certain recursive fashion further terms – called counterterms – such that the resulting modified amplitude – called the renormalized amplitude – is finite at was once given by physicists and is called the BPHZ-procedure .
This procedure justifies itself mainly through the remarkable fact that the numbers obtained from it match certain numbers measured in particle accelerators to fantastic accuracy.
Its combinatorial Hopf-algebraic interpretation
The combinatorial Hopf algebraic approach to perturbative quantum field theory, see for instance
- Hector Figueroa, Jose Gracia-Bondia, Combinatorial Hopf algebras in quantum field theory I (arXiv),
starts with the observation that the BPHZ-procedure can be understood
-
by noticing that there is secretly a natural group structure on the collection of amplitudes;
-
which is induced from the fact that there is secretly a natural Hopf algebra structure on the vector space whose basis consists of graphs;
-
and with respect to which the BPHZ-procedure is simply the Birkhoff decomposition of group valued functions on the circle into a divergent and a finite part.
The Hopf algebra structure on the vector space whose basis consists of graphs can be understood most conceptually in terms of pre-Lie algebras.
The Connes-Kreimer theorem
A Birkhoff decomposition of a loop in a complex group is a continuation of the loop to
-
a holomorphic function on the standard disk inside the circle;
-
a holomorphic function on the complement of this disk in the projective complex plane
-
such that on the unit circle the original loop is reproduced as
with the product and the inverse on the right taken in the group .
Notice that by the assumption of holomorphicity is a well defined element of .
Theorem
(Connes-Kreimer)
-
If is the group of characters on any graded connected commutative Hopf algebra
then the Birkhoff decomposition always exists and is given by the formula
-
There is naturally the structure of a Hopf algebra, , on the graphs considered in quantum field theory. As an algebra this is the free commutative algebra on the “1-particle irreducible graphs”. Hence QFT amplitudes can be regarded as characters on this Hopf algebra.
-
The BPHZ renormalization-procedure for amplitudes is nothing but the first item applied to the special case of the second item.
Proof
The proof is given in
- Alain Connes, Dirk Kreimer, Renormalization in quantum field theory I (arXiv)
The Hopf-algebra perspective on QFT
This result first of all makes Hopf algebra an organizational principle for (re-)expressing familiar operations in quantum field theory.
Computing the renormalization of an amplitude amounts to using the above formula to compute the counterterm and then evaluating the right hand side of
where the product is the group product on characters, hence the convolution product of characters.
Every elegant reformulation has in it the potential of going beyond mere reformulation by allowing to see structures invisible in a less natural formulation. For instance Dirk Kreimer claims that the Hopf algebra language allows him to see patterns in perturbative quantum gravity previously missed.
Gauge theory and BV-BRST with Hopf algebra
Walter von Suijlekom is thinking about the Hopf-algebraic formulation of BRST-BV methods in nonabelian gauge theory
In his nicely readable
he reviews the central idea: the BRST formulation of Yang-Mills theory manifests itself at the level of the resulting bare i.e. unnormalized amplitudes in certain relations satisfied by these, the Slavnov-Taylor identities .
Renormalization of gauge theories is consistent only if these relations are still respected by renormalized amplitudes, too. We can reformulate this in terms of Hopf algebra now:
the relations between amplitudes to be preserved under renormalization must define a Hopf ideal in the Hopf algebra of graphs.
Walter von Suijlekom proves this to be the case for Slavnov-Taylor in his theorem 9 on p. 12
As a payoff, he obtains a very transparent way to prove the generalization of Dyson’s formula to nonabelian gauge theory, which expresses renormalized Green’s functions in terms of unrenormalized Green’s functions “at bare coupling”. This is his corollary 12 on p. 13.
In the context of BRST-BV quantization these statements are subsumed, he says, by the structure encoded in the Hopf ideal which corresponds to imposing the BV-master equation. See also (Suijlekom).
Lattice renormalization
Of theories in BV-CS form
In (Costello 07) a renormalization procedure is discussed that applies to theories that are given by action functionals which can be given in the form
where
-
the fields are sections of a graded field bundle on which is a differential, a compatible antibracket pairing such that is a free field theory (as discussed there) in BV-BRST formalism;
-
is an interaction that is at least cubic.
These are action functionals that are well adapted to BV-BRST formalism and for which there is a quantization to a factorization algebra of observables.
Most of the fundamental theories in physics are of this form, notably Yang-Mills theory. In particular also all theories of infinity-Chern-Simons theory-type coming from binary invariant polynomials are perturbatively of this form, notably ordinary 3d Chern-Simons theory.
For a discussion of just the simple special case of 3d CS see (Costello 11, chapter 5.4 and 5.14).
For comparison of the following with other renormalization schemes, see at (Costello 07, section 1.7).
The setup
Definition
-
A smooth manifold (“spacetime”/“worldvolume”);
-
a -graded complex vector bundle (the “field bundle” containing also in general antifields and ghosts);
-
equipped with a bundle homomorphism (the “antibracket density”)
from the fiberwise tensor product of with itself to the compex density bundle which is fiberwise
-
non-degenerate
-
anti-symmetric
-
of degree -1
-
Write for the space of sections of the field bundle of compact support. Write
for the induced pairing on sections
The paring being non-degenerate means that we have an isomorphism and we write
-
A differential operator on sections of the field bundle
of degree 1 such that
-
is an elliptic complex;
-
is self-adjoint with respect to in that for all fields of homogeneous degree we have .
-
From this data we obtain:
-
The action functional of this corresponding free field theory is
-
The classical BV-complex is the symmetric algebra of sections of equipped with the induced action of the differential and the pairing
Operator (heat) kernels and propagators
Definition
For the corresponding convolution operator is
Definition
For a linear operator, a heat kernel for it is a function such that for each the convolution with , def. , reproduces the exponential of :
Proposition
For a generalized Laplace operator such as the of def. there is a unique heat kernel which is moreover a smooth function of .
Definition
For write
This is (Costello 07, p. 32).
Proposition
The renormalization group operator
Definition
For the gauge fixing operator of def. , and the heat kernel of the corresponding generalized Laplace operator by prop. , write for
The path integral
Proposition
If is the point, then the path integral over the action functional exists as an ordinary integral and is equal to
This is (Costello 07, lemma 6.6.2).
Remark
For of positive dimension, the limit
does not in general exist. Renormalization is the process of adding -corrections to the action – the counterterms – such as to make it exist after all. In this case we may regard the limit, by prop. , as the definition of the path integral.
Renormalized action
The are called the counterterms.
Renormalization
Definition
A renormalization scheme is a decomposition of functions on , as a vector space, into a direct sum
such that the functions are non-singular in that exists.
Hence this is a choice of picking the singularities in functions that are not necessarily defined at .
Theorem
Given any choice of renormalization scheme, def. , there exists a unique choice of counterterms , def. such that
This is (Costello 07, theorem B, p. 38).
Definition
Given a renormalization , write for all
Remark
We think of as the renormalized effective action of the original action at scale .
Examples
Vacuum energy and Cosmological constant
The renormalization freedom in perturbative quantization of gravity (perturbative quantum gravity) induces freedom in the choice of vacuum expectation value of the stress-energy tensor and hence in the cosmological constant.
For details see there.
Chern-Simons level
See at Chern-Simons level renormalization.
Related concepts
References
After the original informal suggestions by Schwinger-Tomonaga-Feynman-Dyson
- Freeman Dyson, The raditation theories of Tomonaga, Schwinger and Feynman, Phys. Rev. 75, 486, 1949 (pdf)
the mathematics of renormalization was finally understood and summarized in the 1975 Erice Majorana School:
- G. Velo and Arthur Wightman (eds.) Renormalization Theory Proceedings of the 1975 Erice summer school, NATO ASI Series C 23, D. Reidel, Dordrecht, 1976
which included causal perturbation theory, BPHZ renormalization, proof of the forest formula? and the BRST complex method for gauge theory.
Little advancement happened until the identification of Hopf algebra structure in the forest formula? due to
- Dirk Kreimer, On the Hopf algebra structure of perturbative quantum field theories, Adv. Theor. Math. Phys. 2 , 303 (1998) (q-alg/9707029)
This finally triggered the formulation of causal perturbation theory in terms of Feynman diagrams in
-
Jose Gracia-Bondia, S. Lazzarini, Connes-Kreimer-Epstein-Glaser Renormalization (arXiv:hep-th/0006106)
-
Kai Keller, chapter IV of Dimensional Regularization in Position Space and a Forest Formula for Regularized Epstein-Glaser Renormalization, PhD thesis (arXxiv:1006.2148)
-
Michael Dütsch, Klaus Fredenhagen, Kai Keller, Katarzyna Rejzner, Dimensional Regularization in Position Space, and a Forest Formula for Epstein-Glaser Renormalization, J. Math. Phy.
55(12), 122303 (2014) (arXiv:1311.5424)
Thus the original “dark art” of the construction of perturbative quantum field theory via renormalization finds a complete rigorous formulation.
In
- Giovanni Collini, Fedosov Quantization and Perturbative Quantum Field Theory (arXiv:1603.09626)
it is shown that (at least under favorable circumstances) the construction of perturbative quantum field theory via causal perturbation theory is equivalently Fedosov deformation quantization of the given interacting Lagrangian density, thus identifying the renormalization freedom with the Freedom in choosing a deformation quantization.
Review
A textbook account of ("re"-)normalization in causal perturbation theory is in
- Michael Dütsch, chapters 3 and 4 of From classical field theory to perturbative quantum field theory, 2018
Informal introductions:
-
G. Peter Lepage, What is Renormalization?, talk 1989 (arXiv:hep-ph/0506330)
-
Steven Weinberg, Effective Field Theory, Past and Future (arXiv:0908.1964)
-
R. E. Borcherds, Renormalization and quantum field theory, (arxiv/1008.0129)
-
Arnold Neumaier, Renormalizatin without infinities – an elementary tutorial (pdf)
Further review:
- V. Mastropietro, Renormalization: general theory, in Encyclopedia of Mathematical Physics 2nd ed, Elsevier (2024) [arXiv:2312.11400]
In causal perturbation theory
The idea of Epstein-Glaser renormalization is due to
- Henri Epstein, Vladimir Glaser, The Role of locality in perturbation theory, Annales Poincaré Phys. Theor. A 19 (1973) 211.
following precursors in
-
Ernst Stückelberg, André Petermann, , La normalisation des constants dans la theorie des quanta, Helv. Phys. Acta 26, 499 (1953); and earlier references therein
(see also Stückelberg-Petermann renormalization group)
-
Nikolay Bogoliubov, Dmitry Shirkov,, Introduction to the Theory of Quantized Fiels, New York: John Wiley and Sons, 1976, 3rd edition
This was formulated in terms of splittings of distributions. The equivalent formulation in terms of extensions of distributions is due to
-
G. Popineau and Raymond Stora, A pedagogical remark on the main theorem of perturbative renormalization theory, Nucl. Phys. B 912 (2016), 70–78, preprint: LAPP–TH, Lyon (1982).
-
Raymond Stora, Differential algebras in Lagrangean field theory, Lectures at ETH, Zürich, 1993, unpublished
-
Romeo Brunetti, Klaus Fredenhagen, Microlocal Analysis and Interacting Quantum Field Theories: Renormalization on Physical Backgrounds, Commun. Math. Phys. 208:623-661 (2000) (arXiv:math-ph/9903028)
Exposition includes
- Christian Brouder, Multiplication of distributions, 2010 (pdf)
The resulting Stückelberg-Petermann renormalization group is due to
- Ernst Stückelberg, André Petermann, La normalisation des constantes dans la theorie des quanta, Helv. Phys. Acta 26 (1953), 499–520
The relation of Epstein-Glaser/Stückelberg-Petermann to the renormalization group flow of
- Murray Gell-Mann and F. E. Low, Quantum Electrodynamics at Small Distances, Phys. Rev. 95 (5) (1954), 1300–1312 (pdf)
and the effective quantum field theory of
-
Kenneth Wilson, Renormalization group and critical phenomena , I., Physical review B 4(9) (1971).
-
Joseph Polchinski, Renormalization and effective Lagrangians , Nuclear Phys. B B231, 1984 (pdf)
is due to
-
Romeo Brunetti, Michael Dütsch, Klaus Fredenhagen, section 5.2 of Perturbative Algebraic Quantum Field Theory and the Renormalization Groups, Adv. Theor. Math. Physics 13 (2009), 1541-1599 (arXiv:0901.2038)
-
Michael Dütsch, Connection between the renormalization groups of Stückelberg-Petermann and Wilson, Confluentes Mathematici, Vol. 4, No. 1 (2012) 12400014 (arXiv:1012.5604)
-
Michael Dütsch, Klaus Fredenhagen, Kai Keller, Katarzyna Rejzner, appendix A of Dimensional Regularization in Position Space, and a Forest Formula for Epstein-Glaser Renormalization, J. Math. Phy. 55(12), 122303 (2014) (arXiv:1311.5424)
Review is in
- Michael Dütsch, section 3.8 of From classical field theory to perturbative quantum field theory, 2018
For more see at perturbation theory – In AQFT.
Applications to the renormalization of Yang-Mills theory on curved background spacetimes is accomplished in
- Stefan Hollands, Renormalized Quantum Yang-Mills Fields in Curved Spacetime, Rev.Math.Phys.20:1033-1172,2008 (arXiv:0705.3340)
BPHZ Renormalization
BPHZ renormalization was introduced in particular in
- Klaus Hepp, Théorie de la Renormalisation Lect. Notes in Phys. Springer (1969)
Review:
-
Klaus Sibold, Bogoliubov-Parasiuk-Hepp-Zimmermann renormalization scheme, Scholarpedia, 5(5):7306. doi:10.4249/scholarpedia.7306
-
Alain Connes, Matilde Marcolli Noncommutative Geometry, Quantum Fields and Motives
-
Michel Talagrand, §16 in: What is a Quantum Field Theory? – A first Introduction for Mathematicians, Cambridge University Press (2022) [doi:10.1017/9781108225144]
The original articles on the Hopf-algebraic formulation:
- Alain Connes, Dirk Kreimer, Renormalization in quantum field theory and the Riemann-Hilbert problem. I. The Hopf algebra structure of graphs and the main theorem, Comm. Math. Phys. 210 (2000), no. 1, 249–273, hep-th/9912092, MR2002f:81070, doi, II. The -function, diffeomorphisms and the renormalization group, Comm. Math. Phys. 216 (2001), no. 1, 215–241; hep-th/0003188, MR2002f:81071, doi
An introduction and review to the Hopf-algebraic description of renormalization is in
- Christian Brouder, Quantum field theory meets Hopf algebra (arxiv:hep-th/0611153)
A textbook treatment is
- Dirk Kreimer, Knots and Fenyman diagrams , Cambridge Lecture Notes in Physics. 13. Cambridge: Cambridge University Press.
- Joseph C. Varilly, The interface of noncommutative geometry and physics, hep-th/0206007
Some heavywheight automated computations using this formalism are discussed in
- D. J. Broadhurst, Dirk Kreimer, Renormalization automated by Hopf algebra (arXiv:hep-th/9810087)
See also
- W. van Suijlekom, Representing Feynman graphs on BV-algebras , (arXiv)
- Dirk Kreimer, Karen Yeats, Diffeomorphisms of quantum fields, arxiv/1610.01837
In BV formalism
Discussion of renormalization in the context of BV-BRST formalism is for relativistic field theory in the rigorous framework of causal perturbation theory/perturbative AQFT due to
-
Klaus Fredenhagen, Kasia Rejzner, Batalin-Vilkovisky formalism in the functional approach to classical field theory, Commun. Math. Phys. 314(1), 93–127 (2012) (arXiv:1101.5112)
-
Klaus Fredenhagen, Kasia Rejzner, Batalin-Vilkovisky formalism in perturbative algebraic quantum field theory, Commun. Math. Phys. 317(3), 697–725 (2012) (arXiv:1110.5232)
-
Katarzyna Rejzner, Batalin-Vilkovisky formalism in locally covariant field theory (arXiv:1111.5130)
-
Katarzyna Rejzner, Remarks on local symmetry invariance in perturbative algebraic quantum field theory (arXiv:1301.7037)
and surveyed in
- Kasia Rejzner, section 7 of Perturbative algebraic quantum field theory Springer 2016 (web)
Discussion for Euclidean field theory is in
building on
- Kevin Costello, Renormalisation and the Batalin-Vilkovisky formalism (arXiv:0706.1533)
See also at factorization algebra of observables.
A vaguely related approach earlier appeared in
- Dmitry Tamarkin, A formalism for the renormalization procedure (arXiv:math/0312219)
On compactified configuration spaces
For Euclidean field theory, an alternative to regarding propagators/time-ordered products/Feynman amplitudes as distributions of several variables with singularities at (in particular) coincident points, one may pullback these distributions to smooth functions on Fulton-MacPherson compactifications of configuration spaces of points and study renormalization in that perspective.
This approach was originally considered specifically for Chern-Simons theory in
- Scott Axelrod, Isadore Singer, Chern–Simons Perturbation Theory II, J. Diff. Geom. 39 (1994) 173-213 (arXiv:hep-th/9304087)
which was re-amplified in
-
Raoul Bott, Alberto Cattaneo, Remark 3.6 in Integral invariants of 3-manifolds, J. Diff. Geom., 48 (1998) 91-133 (arXiv:dg-ga/9710001)
-
Alberto Cattaneo, Pavel Mnev, Remark 11 in Remarks on Chern-Simons invariants, Commun.Math.Phys.293:803-836,2010 (arXiv:0811.2045)
A systematic development of perturbative quantum field theory from this perspective is discussed in
-
Christoph Bergbauer, Romeo Brunetti, Dirk Kreimer, Renormalization and resolution of singularities (arXiv:0908.0633)
-
Christoph Bergbauer, Renormalization and resolution of singularities, talks as IHES and Boston, 2009 (pdf)
-
Marko Berghoff, Wonderful renormalization, 2014 (pdf, doi:10.18452/17160)
-
Marko Berghoff, Wonderful compactifications in quantum field theory, Communications in Number Theory and Physics Volume 9 (2015) Number 3 (arXiv:1411.5583)
For more see at Feynman amplitudes on compactified configuration spaces of points.
Operadic description
- Jean-Louis Loday, Nikolay M. Nikolov, Operadic construction of the renormalization group (arXiv:1202.1206)
Relations to motives, polylogarithms, positivity
-
Alexander Goncharov, Marcus Spradlin, C. Vergu, Anastasia Volovich, Classical polylogarithms for amplitudes and Wilson loops, Phys.Rev.Lett.105:151605,2010 arxiv/1006.5703
-
Nima Arkani-Hamed, Jacob L. Bourjaily, Freddy Cachazo, Alexander Goncharov, Alexander Postnikov, Jaroslav Trnka, Scattering amplitudes and the positive Grassmannian, arxiv/1212.5605
-
Spencer Bloch, Hélène Esnault, Dirk Kreimer, On motives associated to graph polynomials, Commun.Math.Phys. 267 (2006) 181-225 math.AG/0510011 doi
Last revised on April 11, 2024 at 16:49:06. See the history of this page for a list of all contributions to it.