nLab time-ordered product
Context
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
In relativistic perturbative quantum field theory, the time-ordered product is a product on suitably well-behave observables which re-orders its arguments according to the causal ordering of their spacetime supports befor multiplying with the Wick algebra product.
(Analogously reverse causal ordering this is called the reverse-time ordered or anti-time ordered prouct.)
For example for point-evaluation field observables and distinct events the time-ordered product is defined by
This may be understood as arising from the causal additivity-axiom of the perturbative S-matrix. It generalizes the 1-dimensional time-ordering (path ordering) of the Dyson series in quantum mechanics.
More precisely, the time-ordere product is a commutative algebra-structure on the microcausal polynomial observables of a free Lagrangian field theory equipped with a vacuum state (Hadamard state) which on regular polynomial observables given on the regular polynomial observables by the star product which is induced (via this def.) by the Feynman propagator and which is extended from there, in the sense of extensions of distributions, to all microcausal polynomial observables. (This extension is the “renormalization” of the time-ordered product).
Definition
On regular polynomial observables
Definition
(time-ordered product on regular polynomial observables)
Let be a free Lagrangian field theory over a Lorentzian spacetime and with Green-hyperbolic Euler-Lagrange differential equations; write for the induced causal propagator. Let moreover be a compatible Wightman propagator and write for the induced Feynman propagator.
Then the time-ordered product on the space of off-shell regular polynomial observable is the star product induced by the Feynman propagator (via this prop.):
hence
(Notice that this does not descend to the on-shell observables, since the Feynman propagator is not a solution to the homogeneous equations of motion.)
Proposition
(time-ordered product is indeed causally ordered Wick algebra product)
Let be a free Lagrangian field theory over a Lorentzian spacetime and with Green-hyperbolic Euler-Lagrange differential equations; write for the induced causal propagator. Let moreover be a compatible Wightman propagator and write for the induced Feynman propagator.
Then the time-ordered product on regular polynomial observables (def. ) is indeed a time-ordering of the Wick algebra product in that for all pairs of regular polynomial observables
with disjoint spacetime support we have
Here is the causal order relation (“ does not intersect the past cone of ”). Beware that for general pairs of subsets neither nor .
Proof
Recall the following facts:
-
the advanced and retarded propagators by definition are supported in the future cone/past cone, respectively
-
they turn into each other under exchange of their arguments (this cor.):
-
the real part of the Feynman propagator, which by definition is the real part of the Wightman propagator is symmetric (by definition or else by this prop.):
Using this we compute as follows:
Proposition
(time-ordered product on regular polynomial observables isomorphic to pointwise product)
The time-ordered product on regular polynomial observables (def. ) is isomorphism to the pointwise product of observables (this def.) via the linear isomorphism
given by
in that
hence
(Brunetti-Dütsch-Fredenhagen 09, (12)-(13), Fredenhagen-Rejzner 11b, (14))
Proof
Since the Feynman propagator is symmetric (this prop.), the statement is a special case of this prop.).
Example
(time-ordered exponential of regular polynomial observables)
Let
be a regular polynomial observables of degree zero, and write
for the exponential of with respect to the pointwise product.
Then the exponential of with respect to the time-ordered product (def. ) is equal to the conjugation of the exponential with respect to the pointwise product by the time-ordering isomorphism from prop. :
On local observables
The time-ordered product on regular polynomial observables from prop. extends to a product on polynomial local observables, then taking values in microcausal observables:
This extension is not unique. A choice of such an extension, satisfying some evident compatibility conditions, is a choice of renormalization scheme for the given perturbative quantum field theory. Every such choice corresponds to a choice of perturbative S-matrix for the theory. This construction is called causal perturbation theory.
Properties
Relation to path integral
Remark
(operator product order and time-order)
Under the path integral, the order of the product of linear operators (such as as opposed to ) corresponds to temporal ordering of their observable values (Feynman 1948, p. 381, reviewed in Nagaosa 1999, pp. 33; Ong).
Conversely the product of observable values in the path integral corresponds to the time-ordered product of the corresponding linear operators (eg. Polchinski 1998 (A.1.17); Rischke 2021 (5.63)).
Related concepts
| free field algebra of quantum observables | physics terminology | maths terminology | |
|---|---|---|---|
| 1) | supercommutative product | normal ordered product | pointwise product of functionals |
| 2) | non-commutative product (deformation induced by Poisson bracket) | operator product | star product for Wightman propagator |
| 3) | time-ordered product | star product for Feynman propagator | |
| perturbative expansion of 2) via 1) | Wick's lemma  | Moyal product for Wightman propagator | |
| perturbative expansion of 3) via 1) | Feynman diagrams 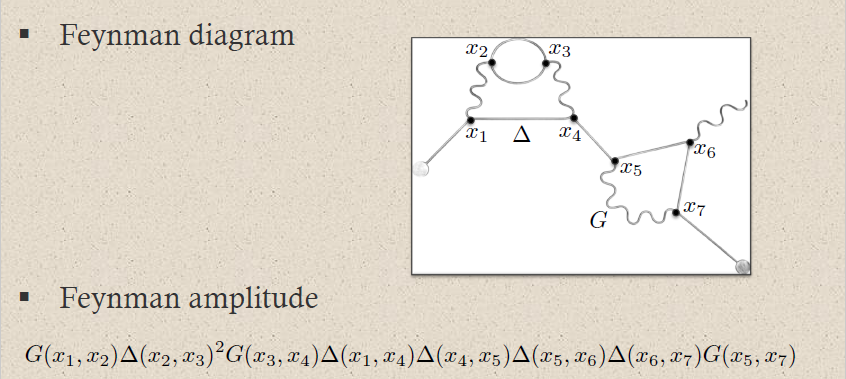 | Moyal product for Feynman propagator |
References
See also the references at S-matrix
The equivalence of the time-ordered product on regular observables to the point-wise product was maybe first highlighted in
- Romeo Brunetti, Michael Dütsch, Klaus Fredenhagen, p. 6 of Perturbative Algebraic Quantum Field Theory and the Renormalization Groups, Adv. Theor. Math. Physics 13 (2009), 1541-1599 (arXiv:0901.2038)
and then further amplified in
- Klaus Fredenhagen, Kasia Rejzner, p. 6 of Batalin-Vilkovisky formalism in perturbative algebraic quantum field theory, Commun. Math. Phys. 317(3), 697–725 (2012) (arXiv:1110.5232)
Last revised on November 24, 2023 at 17:35:18. See the history of this page for a list of all contributions to it.