nLab M5-brane

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Redirected from "M5-branes".
Contents

Context

String theory

Ingredients

Critical string models

Extended objects

Topological strings

Backgrounds

Phenomenology

Contents

Idea

In 11-dimensional supergravity the brane electrically charged under the supergravity C-field is the M2-brane/membrane. The dual under electric-magnetic duality is the M5-brane.

Definition

As a Green-Schwarz type sigma-model

As a Green-Schwarz sigma-model: BLNPST 97

As a black pp-brane

As a black brane solution of 11-dimensional supergravity the M5-brane is given (Gueven 92) by the spacetime ℝ 5,1×(ℝ 5−{0})\mathbb{R}^{5,1} \times (\mathbb{R}^5-\{0\}) with pseudo-Riemannian metric given by

g=H −1/3g ℝ 5,1⊕H 2/3g ℝ 5−{0} g = H^{-1/3} g_{\mathbb{R}^{5,1}} \oplus H^{2/3} g_{\mathbb{R}^5-\{0\}}

for H=1+1rH = 1 + \frac{1}{r} and rr the distance in ℝ 5\mathbb{R}^5 from the origin, and with field strength of the supergravity C-field being

F=⋆ ℝ 5dH. F = \star_{\mathbb{R}^5} \mathbf{d}H \,.

This is a 1/21/2-BPS state of 11-dimensional supergravity.

The near horizon geometry of this spacetime is AdS7×\timesS4. For more on this see at AdS-CFT.

1/2 BPS black branes in supergravity: D-branes, F1-brane, NS5-brane, M2-brane, M5-brane

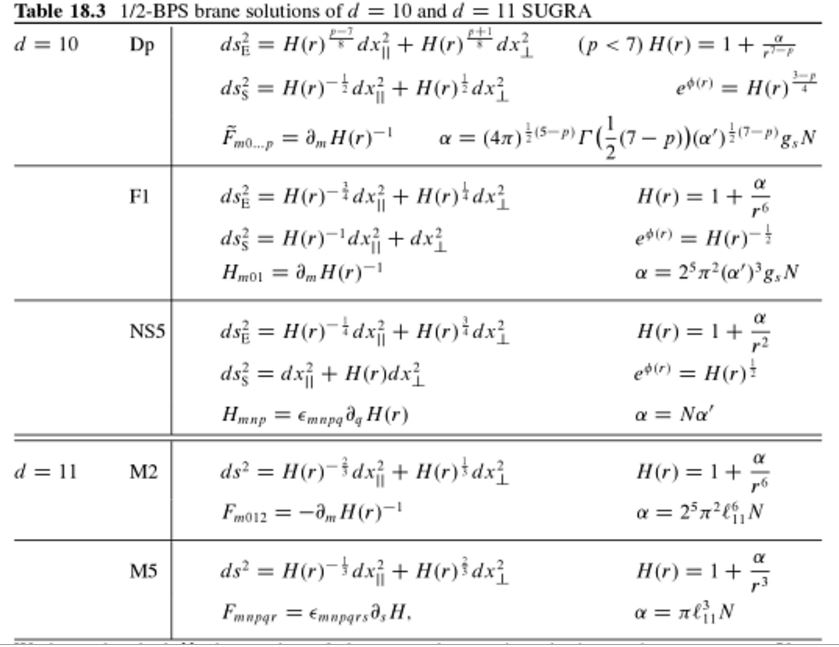
(table from Blumenhagen, Lüst & Theisen 2013, Chapter 18.5)

At an orbifold singularity

More generally for 1/2 BPS black M5-branes, the near horizon geometry is AdS 7×S 4/GAdS_7 \times S^4/G, where GG is a finite subgroup of SU(2) (ADE subgroup) acting by left multiplication on the quaternions ℍ\mathbb{H} in the canonical way, under the identitfication S 4≃S(ℝ 5)≃S(ℝ⊕ℍ)S^4 \simeq S(\mathbb{R}^5) \simeq S(\mathbb{R}\oplus \mathbb{H}) (MFF 12, section 8.3).

While this geometric discussion in MFF 12, section 8.3 works for all the finite subgroups of SU(2), folklore has it that in M-theory the M5-branes appear only at A-type singularities, while the more general 6d (2,0)-superconformal field theories for all possible ADE-singularities appear only after passage to F-theory (ZHTV 14, p. 3).

On the other hand, when placing the M5 at an MO5-orientifold (Witten 95) its worldvolume theory breaks from (2,0)(2,0) to (1,0)(1,0)-supersymmetry and all ADE-singularities should be allowed.

(…)

Properties

Worldvolume theory

the worldvolume theory of the M5-brane is the 6d (2,0)-superconformal QFT.

This worldvolume theory involves self-dual higher gauge theory of the nonabelian kind (Witten07, Witten09): the fields are supposed to be connections on a 2-bundle(∼\sim gerbe), presumably with structure 2-group the automorphism 2-group AUT(G)AUT(G) of some Lie group GG.

For instance in the proposal of (SSW11) one sees in equation (2.1) almost the data of an 𝔞𝔲𝔱(𝔤)\mathfrak{aut}(\mathfrak{g})-Lie 2-algebra valued forms.

Branes inside the M5

The M5-brane admits two solitonic excitations (pp-branes within branes)

See also

Dimensional reduction

On dimensional reduction of 11-dimensional supergravity on a circle the M5-brane turns into the NS5-brane and the D4-brane of type II string theory.

The compactification of the 5-brane on a Riemann surface yields as worldvolume theory N=2 D=4 super Yang-Mills theory. See at N=2 D=4 SYM – Construction by compactification of 5-branes.

Holographic dual

The AdS/CFT correspondence for the 5-brane is AdS 7/CFT 6AdS_7/CFT_6 and relates the 6d (2,0)-superconformal QFT to 7-dimensional supergravity obtained by reduction of 11-dimensional supergravity on a 4-sphere to an asymptotically 7d anti de Sitter spacetime.

Conformal blocks and 7d Chern-Simons dual

The self-dual 2-connection-field (see there for more details) on the 6-dimensional worldvolume M5-brane is supposed to have a holographic description in terms of a 7-dimensional Chern-Simons theory (Witten 1996). We discuss the relevant “fractional” quadratic form on ordinary differential cohomology that defines the correct action functional.

Let G^\hat G be the circle 3-bundle with connection on a 7-dimensional manifold XX with boundary the M5-brane, thought of as the compactification of the supergravity C-field from 11-dimensional supergravity down to 7-dimensional supergravity.

As discussed there, the 7-dimensional Chern-Simons theory action functional on these 3-connections is

G^ 4↦exp(i∫ XG^ 4∪G^ 4), \hat G_4 \mapsto \exp(i \int_X \hat G_4 \cup \hat G_4) \,,

where

The space of states of this 7d theory on the M5 worldvolume ∂X\partial X would be the space of conformal blocks of the 6d (2,0)-supersymmetric QFT on the worldvolume.

Except, that it turns out that the first Chern class of the corresponding prequantum line bundle is twice that required from geometric quantization.

Therefore the above action functional is not yet the correct one, but only a fractional version of it is. However, the class G 4∪G 4G_4 \cup G_4 in integral cohomology has in general no reason to be divisible by 2.

This is related to the fact that as a quadratic form on the ordinary differential cohomology group H^ 4(X)\hat H^4(X), the above is not a quadratic refinement of

(G^,G^′)↦exp(i∫ XG^∪G^′), (\hat G, \hat G') \mapsto \exp(i \int_X \hat G \cup \hat G') \,,

but of twice that. In (Witten 1996) it was argued, and later clarified in (Hopkins-Singer), that instead the action functional should be replaced by a proper quadratic refinement.

This is accomplished by shifting the center of the quadratic form by a lift λ∈H 4(X,ℤ)\lambda \in H^4(X, \mathbb{Z}) of the degree-4 Wu class ν 4∈H 4(X,ℤ/2)\nu_4 \in H^4(X, \mathbb{Z}/2) from 0 to 12λ\frac{1}{2}\lambda.

(For that to make sense in integral cohomology, either the Wu class λ\lambda happens to be divisible by 2 on XX, or else one has to regard it itself as a twisted differential character of sorts, as explained in (Hopkins-Singer). For the moment we will assume that XX is such that λ\lambda is divisbible by 2.)

Since XX, being a spacetime for supergravity, admits (and is thought to be equipped with) a spin structure, by the discussion at Wu class it follows that λ\lambda is the first fractional Pontryagin class 12p 1\frac{1}{2}p_1

(12p 1mod2)=ν 4∈H 4(X,ℤ/2). (\frac{1}{2}p_1 \; mod \; 2) \; = \; \nu_4 \in H^4(X, \mathbb{Z}/2) \,.

By the very definition of Wu class, it follows that for any α^∈H^ 4(X)\hat \alpha \in \hat H^4(X) the combination

α^∪α^+α^∪λ^=Sq 4(α^)−α^∪λ^=0mod2 \hat \alpha \cup \hat \alpha + \hat \alpha \cup \hat \lambda = Sq^4(\hat \alpha) - \hat \alpha \cup \hat \lambda \; =\; 0 \; mod \; 2

is divisible by 2.

Therefore define then the modified quadratic form

exp(iS λ):a^↦expi∫ X12(a^∪a^+a^∪λ^) \exp(i S^\lambda) \; : \; \hat a \mapsto \exp i \int_X \frac{1}{2} \left( \hat a \cup \hat a + \hat a \cup \hat \mathbf{\lambda} \right)

(see differential string structure for the definition of the differential refinement λ^=12p^ 1\hat \mathbf{\lambda} = \frac{1}{2}\hat \mathbf{p}_1), where, note, we have included a global factor of 2, which is now possible due to the inclusion of the integral lift of the Wu class.

Notice that where the equations of motion of the original action functional are a^=0\hat a = 0, those of this shifted one are a^=−12λ^\hat a = - \frac{1}{2}\hat \mathbf{\lambda}. One may therefor calls −12λ-\frac{1}{2}\lambda here a background charge for the 7-d Chern-Simons theory.

This is now indeed a quadratic refinement of the intersection pairing:

expi(S λ(a^+b^)−S λ(a^)−S λ(b^)+S λ(0))=expi∫ X(a^∪b^). \exp i \left( S^\lambda\left(\hat a + \hat b \right) - S^\lambda\left( \hat a \right) - S^\lambda\left( \hat b \right) + S^\lambda\left( 0 \right) \right) = \exp i \int_X ( \hat a \cup \hat b ) \,.

To express the correct action functional for the 7d Chern-Simons theory it is useful to define the shifted supergravity C-field

a^:=G^ 4−12λ^, \hat a := \hat G_4 - \frac{1}{2}\hat \mathbf{\lambda} \,,

which the object whose equations of motion with respect to the 7d Chern-Simons theory are still a^=0\hat a = 0.

Then in terms of the original G^ 4\hat G_4 the action functional for the holographic dual 7d Chern-Simons theory reads

exp(iS(G^ 4))=exp(i∫ X12(G^ 4∪G^ 4−(12λ^) 2)). \exp(i S(\hat G_4)) = \exp(i \int_X \frac{1}{2} ( \hat G_4 \cup \hat G_4 - (\frac{1}{2}\hat \mathbf{\lambda})^2 ) ) \,.

This is the action as it appears in (Witten96, (3.6)).

In terms of twisted differential c-structures we may summarize the outcome of this reasoning as follows:

The divisibility of the action functional requires a 2(G 4−a)2(G_4 - a)-twisted Wu structure in ℤ/2\mathbb{Z}/2-cohomology. Its lift to integral cohomology is the 2(G 4−a)2(G_4 - a)-twisted differential string structure known as the “Witten quantization condition” on the supergravity C-field.

Restriction of the supergravity CC-field

We discuss the conditions on the restriction of the supergravity C-field on the ambient 11-dimensional supergravity spacetime to the M5-brane.

This is similar to the analogous situation in type II string theory. The Freed-Witten anomaly cancellation condition demands that the restriction of the B-field H^ 3H^ 3(X)\hat H_3 \hat H^3(X) on spacetime XX to an oriented D-brane Q↪XQ \hookrightarrow X has to trivialize, up to torsion, relative to the integral Stiefel-Whitney class W 3=β(w 2)W_3 = \beta(w_2), where β\beta is the Bockstein homomorphism induced from the short exact sequence ℤ→⋅2ℤ→ℤ 2\mathbb{Z} \stackrel{\cdot 2}{\to} \mathbb{Z} \to \mathbb{Z}_2:

H 3| Q≃W 3, H_3|_Q \simeq W_3 \,,

thus defining a twisted spin^c-structure? on the D-brane.

The analog of this for the M5-brane is discussed in (Witten00, section 5). There it is argued that there is a class

θ∈H 3(Q,U(1)) \theta \in H^3(Q, U(1))

on the 5-brane such that under the Bockstein homomorphism β′\beta' induced by the short exact sequence ℤ→ℝ→U(1)\mathbb{Z} \to \mathbb{R} \to U(1) we have for the supergravity C-field G^∈H^ 4(X)\hat G \in \hat H^4(X) the condition

G| Q=β′(θ). G|_Q = \beta'(\theta) \,.

By the above quantization condition, this may also be thought of as witnessing a twisted string structure on the 5-brane (Sati).

This condition reduces to the above one for the BB-field under double dimensional reduction on the circle.

M5-brane charge

See at M5-brane charge


Anomaly cancellation

Consider a 2-parameter family X (11)X^{(11)} of 11-dimensional spin-manifolds and a 2-parameter family Q M5↪X (11)Q_{M5} \hookrightarrow X^{(11)} of 6-dimensional submanifolds. When regarded as a family of worldvolumes of an M5-brane, the family of normal bundles N XQ M5N_X Q_{M5} of this inclusion carries a characteristic class

(1)I M5≔I ψ M5+I C∈H 8(F×Q M5,ℤ) I^{M5} \;\coloneqq\; I^{M5}_{\psi} + I_{C} \;\in\; H^8(F \times Q_{M5},\mathbb{Z})

where

  1. the first summand is the class of the chiral anomaly of chiral fermions on Q M5Q_{M5} (Witten 96, (5.1)),

  2. the second term the class of the quantum anomaly of a self-dual higher gauge field (Witten 96, (5.4))

Moreover, there is the restriction of the I8-term (see there) to Q M5Q_{M5}, hence to the tangent bundle of X 11X^{11} to Q M5Q_{M5} (the “anomaly inflow” from the bulk spacetime to the M5-brane)

(2)I 8| M5≔I 8(T Q M5X)∈H 8(F×Q M5,ℤ). I_8\vert_{M5} \;\coloneqq\; I_8 \big( T_{Q_{M5}} X \big) \;\in\; H^8(F \times Q_{M5},\mathbb{Z}) \,.

The sum of these cohomology classes, evaluated on the fundamental class of Q M5Q_{M5} is proportional to the second Pontryagin class of the normal bundle

(3)I M5+I 8| M5=124p 2(N Q M5) I^{M5} \;+\; I_8\vert_{M5} \;=\; \tfrac{1}{24} p_2(N_{Q_{M5}})

(Witten 96 (5.7))

This result used to be “somewhat puzzling” (Witten 96, p. 35) since consistency of the M5-brane in M-theory should require its total quantum anomaly to vanish. But p 2(N Q M5)p_2(N_{Q_{M5}}) does not in general vanish, and the right conditions to require under which it does vanish were “not clear” (Witten 96, p. 37).

(For more details on computations involved in this and the following arguments, see also Bilal-Metzger 03).

A resolution was proposed in Freed-Harvey-Minasian-Moore 98, also Bah-Bonetti-Minasian-Nardoni 18 (5), BBMN 19 (2.9) and appendix A.4, A.5. By this proposal, the anomaly inflow from the bulk would not be just I 8I_8, as in (2) but would be all of the following fiber integration

(4)π *(−16G 4G 4G 4+G 4I 8) =−124p 2+12([G 4 M5]) 2+I 8 \array{ \pi_\ast \Big( - \tfrac{1}{6} G_4 G_4 G_4 + G_4 I_8 \Big) & = - \tfrac{1}{24} p_2 + \tfrac{1}{2}([G^{M5}_4])^2 + I_8 }

Here we used (by this Prop) that

π *(χ 3)=2p 2, \pi_\ast\big( \chi^3 \big) \;=\; 2 p_2 \,,

which would thus cancel against the first term 124p 2\tfrac{1}{24} p_2 in (4). Hence with this proposal, the previously remaining M5-brane anomaly (3) would be canceled… except for yet one last remaining term (shown as ∝γ 4 2\propto \gamma_4^2 in BBMN 19b (4.9), (4.13), (5.22)):

(5)[G 4 M5] 2∈H 8(Q M5;ℤ), [G^{M5}_4]^2 \;\in\; H^8(Q_{M5}; \mathbb{Z}) \,,

where

(6)G 4 M5≔(G 4) basic∈Ω dR 4(Q M4) G_4^{M5} \;\coloneqq\; (G_4)_{basic} \;\in\; \Omega^4_{dR}\big( Q_{M4}\big)

denotes the basic form-component of G 4G_4 with respect to the given spherical fibration.

This basic form component G 4 M5G_4^{M5} (6) had been ignored in FHMM 98 and previous references. That this basic form component G 4 M5G_4^{M5} (6) indeed needs to be considered was pointed out in FSS 19v1, (19), BBMN 19b, (3.16) & App. C (where it is denoted γ 4\gamma_4, see also BBM 20 (2.3)) and SS 20, (3) & p. 5.

See also at M-theory – Open problems – M5-brane anomaly cancellation.

The observation that the remaing anomaly (5) vanishes if one assumes Hypothesis H is SS 20, Cor. 6.


M2-M5 brane bound states in the BMN matrix model

There is the suggestion (MSJVR 02, checked in AIST 17a, AIST 17b) that, in the BMN matrix model, supersymmetric M2-M5-brane bound states are identified with isomorphism classes of certain “limit sequences” of longitudinal-light cone-constant N×NN \times N-matrix-fields constituting finite-dimensional complex Lie algebra representations of su(2).

Traditional discussion

Concretely, if

⊕i(N i (M2)⋅N i (M5))∈𝔰𝔲(2) ℂRep fin \underset{ i }{\oplus} \big( N^{(M2)}_i \cdot \mathbf{N}^{(M5)}_i \big) \;\;\in\;\; \mathfrak{su}(2)_{\mathbb{C}}Rep^{fin}

denotes the representation containing

of the

  • N i (M5)N^{(M5)}_i-dimensional irrep N i (M5)∈𝔰𝔲(2) ℂRep\mathbf{N}^{(M5)}_i \in \mathfrak{su}(2)_{\mathbb{C}}Rep

(for {N i (M2),N i (M5)} i∈(ℕ×ℕ) I\{N^{(M2)}_i, N^{(M5)}_i\}_{i} \in (\mathbb{N} \times \mathbb{N})^I some finitely indexed set of pairs of natural numbers)

with total dimension

N≔dim(⊕i(N i (M2)⋅N i (M5))) N \;\coloneqq\; dim \big( \underset{ i }{\oplus} \big( N^{(M2)}_i \cdot \mathbf{N}^{(M5)}_i \big) \big)

then:

  1. a configuration of a finite number of stacks of coincident M5-branes corresponds to a sequence of such representations for which

    1. N i (M2)→∞N^{(M2)}_i \to \infty (this being the relevant large N limit)

    2. for fixed N i (M5)N^{(M5)}_i (being the number of M5-branes in the iith stack)

    3. and fixed ratios N i (M2)/NN^{(M2)}_i/N (being the charge/light-cone momentum carried by the iith stack);

  2. an M2-brane configuration corresponds to a sequence of such representations for which

    1. N i (M5)→∞N^{(M5)}_i \to \infty (this being the relevant large N limit)

    2. for fixed N i (M2)N^{(M2)}_i (being the number of M2-brane in the iith stack)

    3. and fixed ratios N i (M5)/NN^{(M5)}_i/N (being the charge/light-cone momentum carried by the iith stack)

for all i∈Ii \in I.

Hence, by extension, any other sequence of finite-dimensional 𝔰𝔲(2)\mathfrak{su}(2)-representations is a kind of mixture of these two cases, interpreted as an M2-M5 brane bound state of sorts.

Formalization via weight systems on chord diagrams

To make this precise, let

𝔰𝔲(2) ℂMetMod /∼∈Set \mathfrak{su}(2)_{\mathbb{C}} MetMod_{/\sim} \;\in\; Set

be the set of isomorphism classes of complex metric Lie representations (hence finite-dimensional representations) of su(2) (hence of the special linear Lie algebra 𝔰𝔩(2,C)\mathfrak{sl}(2,C)) and write

Span(𝔰𝔲(2) ℂMetMod /∼)∈Vect ℂ Span \big( \mathfrak{su}(2)_{\mathbb{C}} MetMod_{/\sim} \big) \;\in\; Vect_{\mathbb{C}}

for its linear span (the complex vector space of formal linear combinations of isomorphism classes of metric Lie representations).

Finally, write

Span(𝔰𝔲(2) ℂMetMod /∼) ⟶ (𝒲 s) deg c 1⋅V 1+c 2⋅V 2 ↦ c 1⋅w V 1+c 2⋅w V 2 \array{ Span \big( \mathfrak{su}(2)_{\mathbb{C}}MetMod_{/\sim} \big) & \longrightarrow & \big( \mathcal{W}^{{}^{s}} \big)^{deg} \\ c_1 \cdot V_1 + c_2 \cdot V_2 &\mapsto& c_1 \cdot w_{V_1} + c_2 \cdot w_{V_2} }

for the linear map which sends a formal linear combination of representations to the weight system on Sullivan chord diagrams with deg∈ℕdeg \in \mathbb{N} chords which is given by tracing in the given representation.

Then a M2-M5-brane bound state as in the traditional discussion above, but now formalized as an su(2)-weight system

Ψ {N i (M2),N i (M5)} i∈∏deg∈ℕ(𝒲 s) deg \Psi_{ \left\{ N^{(M2)}_i, N^{(M5)}_i \right\}_{i} } \;\in\; \underset{ deg \in \mathbb{N} }{\prod} \big( \mathcal{W}^{{}^{\mathrm{s}}} \big)^{deg}

hence a weight system horizontal chord diagrams closed to Sullivan chord diagrams, these now being the multi-trace observables on these) is

(7)Ψ {N i (M2),N i (M5)} i≔4π2 2deg∑ iN i (M2)∑i(N i (M2)⋅1((N i (M5)) 2−1) 1+2degN i (M5)) \Psi_{ \left\{ N^{(M2)}_i, N^{(M5)}_i \right\}_{i} } \;\coloneqq\; \tfrac{ 4 \pi \, 2^{2\,deg} }{ \sum_i N^{(M2)}_i } \underset{i}{\sum} \left( N^{(M2)}_i \cdot \tfrac{1}{ \left( \sqrt{ \left( N^{(M5)}_i \right)^2 - 1 } \right)^{1 + 2 deg} } \mathbf{N}^{(M5)}_i \right)

(from Sati-Schreiber 19c)

Normalization and large NN limit. The first power of the square root in (7) reflects the volume measure on the fuzzy 2-sphere (by the formula here), while the power of 2deg2\,deg (which is the number of operators in the multi-trace observable evaluating the weight system) gives the normalization (here) of the functions on the fuzzy 2-sphere.

Hence this normalization is such that the single-trace observables among the multi-trace observables, hence those which come from round chord diagrams, coincide on those M2-M5 brane bound states Ψ {N i (M2),N i (M5)} i \Psi_{ \left\{ N^{(M2)}_i, N^{(M5)}_i \right\}_{i} } for which N i (M2)=δ i i 0N (M2)N^{(M2)}_i = \delta_i^{i_0} N^{(M2)}, hence those which have a single constitutent fuzzy 2-sphere, with the shape observables on single fuzzy 2-spheres discussed here:

(from Sati-Schreiber 19c)

Therefore, with this normalization, the limits N (M2)→∞N^{(M2)} \to \infty and N (M5)→∞N^{(M5)} \to \infty of (7) should exist in weight systems. The former trivially so, the latter by the usual convergence of the fuzzy 2-sphere to the round 2-sphere in the large N limit.

Notice that the multi trace observables on these states only see the relative radii of the constitutent fuzzy 2-spheres: If N i (M2)=δ i i 0N (M2)N^{(M2)}_i = \delta_i^{i_0} N^{(M2)} then the N (M2)N^{(M2)}-dependence of (7) cancels out, reflecting the fact that then there is only a single constituent 2-sphere of which the observable sees only the radius fluctuations, not the absolute radius (proportional to N (M2)N^{(M2)}).


gauge theory induced via AdS-CFT correspondence

M-theory perspective via AdS7-CFT6F-theory perspective
11d supergravity/M-theory
↓\;\;\;\;\downarrow Kaluza-Klein compactification on S 4S^4compactificationon elliptic fibration followed by T-duality
7-dimensional supergravity
↓\;\;\;\;\downarrow topological sector
7-dimensional Chern-Simons theory
↓\;\;\;\;\downarrow AdS7-CFT6 holographic duality
6d (2,0)-superconformal QFT on the M5-brane with conformal invarianceM5-brane worldvolume theory
↓\;\;\;\; \downarrow KK-compactification on Riemann surfacedouble dimensional reduction on M-theory/F-theory elliptic fibration
N=2 D=4 super Yang-Mills theory with Montonen-Olive S-duality invariance; AGT correspondenceD3-brane worldvolume theory with type IIB S-duality
↓\;\;\;\;\; \downarrow topological twist
topologically twisted N=2 D=4 super Yang-Mills theory
↓\;\;\;\; \downarrow KK-compactification on Riemann surface
A-model on Bun GBun_G, Donaldson theory

\,

gauge theory induced via AdS5-CFT4
type II string theory
↓\;\;\;\;\downarrow Kaluza-Klein compactification on S 5S^5
↓\;\;\;\; \downarrow topological sector
5-dimensional Chern-Simons theory
↓\;\;\;\;\downarrow AdS5-CFT4 holographic duality
N=4 D=4 super Yang-Mills theory
↓\;\;\;\;\; \downarrow topological twist
topologically twisted N=4 D=4 super Yang-Mills theory
↓\;\;\;\; \downarrow KK-compactification on Riemann surface
A-model on Bun GBun_G and B-model on Loc GLoc_G, geometric Langlands correspondence

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

branein supergravitycharged under gauge fieldhas worldvolume theory
black branesupergravityhigher gauge fieldSCFT
D-branetype IIRR-fieldsuper Yang-Mills theory
(D=2n)(D = 2n)type IIA\,\,
D(-2)-brane\,\,
D0-brane\,\,BFSS matrix model
D2-brane\,\,\,
D4-brane\,\,D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane\,\,D=7 super Yang-Mills theory
D8-brane\,\,
(D=2n+1)(D = 2n+1)type IIB\,\,
D(-1)-brane\,\,\,
D1-brane\,\,2d CFT with BH entropy
D3-brane\,\,N=4 D=4 super Yang-Mills theory
D5-brane\,\,\,
D7-brane\,\,\,
D9-brane\,\,\,
(p,q)-string\,\,\,
(D25-brane)(bosonic string theory)
NS-branetype I, II, heteroticcircle n-connection\,
string\,B2-field2d SCFT
NS5-brane\,B6-fieldlittle string theory
D-brane for topological string\,
A-brane\,
B-brane\,
M-brane11D SuGra/M-theorycircle n-connection\,
M2-brane\,C3-fieldABJM theory, BLG model
M5-brane\,C6-field6d (2,0)-superconformal QFT
M9-brane/O9-planeheterotic string theory
M-wave
topological M2-branetopological M-theoryC3-field on G₂-manifold
topological M5-brane\,C6-field on G₂-manifold
S-brane
SM2-brane,
membrane instanton
M5-brane instanton
D3-brane instanton
solitons on M5-brane6d (2,0)-superconformal QFT
self-dual stringself-dual B-field
3-brane in 6d

References

Survey

The history as of the 1990 is reviewed in:

Further reviews and general accounts include

Black brane description

Unwrapped

The M5 was first found as a black brane of 11-dimensional supergravity (the black fivebrane) in:

see also

That this metric, as well as that of every black pp brane for odd pp, is completely non-singular was observed in

Classification of more general M5-brane ADE-singularities is in

also to some extent in

  • Changhyun Ahn, Kyungho Oh, Radu Tatar, Orbifolds AdS 7×S 4AdS_7 \times S^4 and Six Dimensional (0,1)(0, 1) SCFT, Phys. Lett. B442 (1998) 109-116 (arXiv:hep-th/9804093)

but see p. 3 of

Identification of the 𝒩=(2,0)\mathcal{N} = (2,0) black M5-brane sitting at the A-type singularity of an MO5MO5 ℤ/2\mathbb{Z}/2-orientifold locally of the form ℝ 5,1×(ℝ 5⫽(ℤ/2))\mathbb{R}^{5,1} \times ( \mathbb{R}^5 \sslash (\mathbb{Z}/2) ) is due to

Discussion in terms of E11-U-duality and current algebra is in

Further solutions:

Wrapped on hyperbolic 3-manifolds

Solutions to D=11 N=1 supergravity describing black M5-branes wrapped on hyperbolic 3-manifolds (with application to the 3d-3d correspondence and proof of the volume conjecture):

Discussion of the volume conjecture by combining the 3d/3d correspondence with AdS/CFT in these backgrounds:

Enhanced to a defect field theory:

  • Dongmin Gang, Nakwoo Kim, Mauricio Romo, Masahito Yamazaki, Aspects of Defects in 3d-3d Correspondence, J. High Energ. Phys. (2016) (arXiv:1510.05011)

Wrapped on orbifolds

  • Pietro Ferrero, Jerome P. Gauntlett, Dario Martelli, James Sparks, M5-branes wrapped on a spindle (arXiv:2105.13344)

σ\sigma-Model description

The Green-Schwarz action functional-type sigma-model of the (single) M5-brane of was found in covariant form in

generally following

and using the covariant mechanism for self-dual higher gauge fields from

based on the non-covariant form of the self-duality mechanism (Perry-Schwarz action) due to

Discussion of the equivalence of these superficially different action functionals is in

The equations of motion in super spacetime were derived in

and using the superembedding approach in

see

Amplification that the resulting B-field on the M5-brane is not naively self-dual:

A variant adapted to a 3+3-dimensional split in

The computation of the small fluctuations of this GS-type sigma-model around a solution embedding as the asymptotic boundary of the AdS-spacetime near-horizon geometry of a black 5-brane as above, and the proof, to low order, that the result is the 6d (2,0)-supersymmetric QFT appearing in AdS7-CFT6 duality is due to

A review with emphasis on the coupling to the M2-brane:

Further developments:

M5-branes in the BMN matrix model

On light cone transversal M5-branes and M2-M5 brane bound states in the BMN matrix model:

The proposal of passing to horizontal/vertical limits of sizes of partitions is due to:

A detailed check is in:

Review in:

In a limit where aspects of little string theory on NS5-branes becomes visible:

Worldvolume theory

The original article suggesting the description of the self-dual higher gauge theory on the 5-brane holographically by a dual higher dimensional Chern-Simons theory:

Proposal for a mathematical formulation:

A discussion that embeds this argument into the larger context of AdS-CFT duality:

Discussion of effective non-commutative geometry on M5-brane worldvolumes induced from a constant B-field flux density:

and relating this to aspects of the quantum Hall effect:

Discussion of S-duality in 6d self-dual higher gauge theory via non-commutative-deformation:

See also the references at 6d (2,0)-supersymmetric QFT.

A proposal for a construction as a higher gauge theory for string 2-connections is due to

based on

Discussion in the D'Auria-Fré formulation:

Knot invariants via topological strings and 5-branes

On realization of knot invariants/knot homology via topological string theory and BPS states:

Understanding this via NS5-branes/M5-branes:

Review:

An alternative approach:

Hopf-Wess-Zumino term

The higher WZW term of the M5-brane (Hopf-Wess-Zumino term) was first proposed in

and had been settled by the time of

The resemblence of the first summand of the term to the Whitehead integral formula for the Hopf invariant was noticed in

which hence introduced the terminology “Hopf-Wess-Zumino term”. Followup to this terminology includes

More on the relation to the Hopf invariant in

Discussion of the full 6d WZ term is in

Anomaly cancellation

The original computation of the total M5-brane anomaly due to

left a remnant term of 124p 2\tfrac{1}{24} p_2. It was argued in

that this term disappears (cancels) when properly taking into account the singularity of the supergravity C-field at the locus of the black M5-brane.

This argument is recalled in

The observation that the basic form component G 4 M5G_4^{M5} needs to be discussed is due to:

Double dimensional reduction to D4-brane

The relation of the M5-brane to the D4-brane and the D=5 super Yang-Mills theory in its worldvolume theory by double dimensional reduction:

See also (Witten 11).

Open M5-branes

Discussion of open M5-branes stretching between M9-branes and ending in a Yang monopole:

The corresponding non-supersymmetric 4-branes as seen in heterotic string theory:

Nonabelian 2-form fields

The fact that the worldvolume theory of the M5-brane should support fields that are self-dual connections on a 2-bundle (∼\sim a gerbe) is discussed in

as well as sections 3 and 4 of

Proposals for how to implement this are for instance in

A formal proposal is here.

More on the holographic description

More on the algebraic topology

Last revised on December 7, 2024 at 15:34:56. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (135 revisions) Cite Print Source