nLab double dimensional reduction

Idea

What is called double dimensional reduction is a variant of Kaluza-Klein mechanism combined with fiber integration in the presence of branes: given a spacetime of dimension $d+1$ in which a $p+1$-brane propagates, its KK-reduction results in a $d$-dimensional effective spacetime containing a $p+1$-brane together with a “doubly reduced” $p$-brane, which is the reduction of those original $(p+1)$-brane configurations that wrapped the cycle along which the KK-reduction takes place.

Definition

Via fiber integration in ordinary differential cohomology

Let $\mathbf{H}$ be the smooth topos. For $p+1 \in \mathbb{N}$ write $\mathbf{B}^{p+1}U(1)_{conn} \in \mathbf{H}$ for the universal moduli stack of circle n-bundles with connection (given by the Deligne complex).

Notice that fiber integration in ordinary differential cohomology has the following stacky incarnation (see here):

Proposition

For $\Sigma$ an oriented closed manifold of dimension $k \leq p+1$, then fiber integration in ordinary differential cohomology is reflected by a morphism of the form

$$\array{ [\Sigma, \mathbf{B}^{p+1}U(1)_{conn}] &\stackrel{\int_\Sigma}{\longrightarrow}& \mathbf{B}^{p+1-k}U(1)_{conn} \\ \downarrow^{[\Sigma,curv]} && \downarrow^{curv} \\ [\Sigma,\mathbf{\Omega}^{p+2}] &\stackrel{\int_\Sigma}{\longrightarrow}& \mathbf{\Omega}^{p+2-k} } \,,$$

where the vertical morphisms are the curvature maps and the bottom morphisms reflects ordinary fiber integration of differential forms.

Definition

Given a cocycle

$$\nabla \;\colon\; X \times \Sigma \longrightarrow \mathbf{B}^{p+1}U(1)_{conn} \,,$$

on the Cartesian product of some smooth space $X$ with $\Sigma$, then its double dimensional reduction is the cocycle on $X$ which is given by the composite

$$X \longrightarrow [\Sigma, X \times \Sigma] \stackrel{[\Sigma,\nabla]}{\longrightarrow} [\Sigma,\mathbf{B}^{p+1}U(1)_{conn}] \stackrel{\int_\Sigma}{\longrightarrow} \mathbf{B}^{p+1-k}U(1)_{conn} \,,$$

where the first morphism is the unit of the (Cartesian product $\dashv$ internal hom)-adjunction.

Via cyclic loop spaces

We discuss here a formalization of double dimensional reduction via cyclification adjunction (FSS 16, section 3, BMSS 18, section 2.2). For more see at geometry of physics – fundamental super p-branes the section on double dimensional reduction.

Proposition

Let $\mathbf{H}$ be any (∞,1)-topos and let $G$ be an ∞-group in $\mathbf{H}$. Then the right base change/dependent product along the canonical point inclusion $\ast \to \mathbf{B}G$ into the delooping of $G$ takes the following form: There is a pair of adjoint ∞-functors of the form

$$\mathbf{H} \underoverset {\underset{[G,-]/G}{\longrightarrow}} {\overset{hofib}{\longleftarrow}} {\bot} \mathbf{H}_{/\mathbf{B}G} \,,$$

where

• $[G,-]$ denotes the internal hom in $\mathbf{H}$,

• $[G,-]/G$ denotes the homotopy quotient by the conjugation ∞-action for $G$ equipped with its canonical ∞-action by left multiplication and the argument regarded as equipped with its trivial $G$-$\infty$-action (for $G = S^1$ the circle group this is the cyclic loop space construction).

Hence for

• $\hat X \to X$ a $G$ principal ∞-bundle

• $A$ a coefficient object, such as for some differential generalized cohomology theory

then there is a natural equivalence

$$\underset{ \text{original} \atop \text{fluxes} }{ \underbrace{ \mathbf{H}(\hat X\;,\; A) } } \;\; \underoverset {\underset{oxidation}{\longleftarrow}} {\overset{reduction}{\longrightarrow}} {\simeq} \;\; \underset{ \text{doubly} \atop { \text{dimensionally reduced} \atop \text{fluxes} } }{ \underbrace{ \mathbf{H}_{/\mathbf{B}G}(X \;,\; [G,A]/G) } }$$

given by

$$\left( \hat X \longrightarrow A \right) \;\;\; \leftrightarrow \;\;\; \left( \array{ X && \longrightarrow && [G,A]/G \\ & \searrow && \swarrow \\ && \mathbf{B}G } \right)$$

Proof

First observe that the conjugation action on $[G,X]$ is the internal hom in the (∞,1)-category of $G$-∞-actions $Act_G(\mathbf{H})$. Under the equivalence of (∞,1)-categories

$$Act_G(\mathbf{H}) \simeq \mathbf{H}_{/\mathbf{B}G}$$

(from NSS 12) then $G$ with its canonical ∞-action is $(\ast \to \mathbf{B}G)$ and $X$ with the trivial action is $(X \times \mathbf{B}G \to \mathbf{B}G)$.

Hence

$$[G,X]/G \simeq [\ast, X \times \mathbf{B}G]_{\mathbf{B}G} \;\;\;\;\; \in \mathbf{H}_{/\mathbf{B}G} \,.$$

Actually, this is the very definition of what $[G,X]/G \in \mathbf{H}_{/\mathbf{B}G}$ is to mean in the first place, abstractly.

But now since the slice (∞,1)-topos $\mathbf{H}_{/\mathbf{B}G}$ is itself cartesian closed, via

$$E \times_{\mathbf{B}G}(-) \;\;\; \dashv \;\;\; [E,-]_{\mathbf{B}G}$$

it is immediate that there is the following sequence of natural equivalences

$$\begin{aligned} \mathbf{H}_{/\mathbf{B}G}(Y, [G,X]/G) & \simeq \mathbf{H}_{/\mathbf{B}G}(Y, [\ast, X \times \mathbf{B}G]_{\mathbf{B}G}) \\ & \simeq \mathbf{H}_{/\mathbf{B}G}( Y \times_{\mathbf{B}G} \ast, \underset{p^\ast X}{\underbrace{X \times \mathbf{B}G }} ) \\ & \simeq \mathbf{H}( \underset{hofib(Y)}{\underbrace{p_!(Y \times_{\mathbf{B}G} \ast)}}, X ) \\ & \simeq \mathbf{H}(hofib(Y),X) \end{aligned}$$

Here $p \colon \mathbf{B}G \to \ast$ denotes the terminal morphism and $p_! \dashv p^\ast$ denotes the base change along it.

Examples

Reduction on the circle

Example

When $\Sigma = S^1$ is the circle, and we think of $X \times S^1$ as a spacetime of 11-dimensional supergravity, then $\nabla \colon X \times S^1 \to \mathbf{B}^3 U(1)_{conn}$ may represent the supergravity C-field as a cocycle in ordinary differential cohomology. Then its double dimensional reduction in the sense of def. is the differential cocycle representing the B-field on $X$, in the sense of string theory.

Remark

For $\Sigma = S^1$ a circle as in example , then the morphism $X \longrightarrow [\Sigma, X \times \Sigma]$ in def. sends each point of $X$ to the loop in $X\times S^1$ that winds identically around the copy of $S^1$ at that point. Hence in this case it would make sense to consider, more generally, for each $p \in \mathbb{Z}$ the “order $p$” double dimensional reduction, given by the operation where one instead considers the map that lets the loop wind $p$ times around the $S^1$.

The resulting double dimensional reduction is just $p$-times the original one, so in a sense nothing much is changed, but maybe it is suggestive that now we are looking at the space of $C_p$-fixed points of the free loop space (for $C_p$ the cyclic group of order $p$). In E-infinity geometry this fixed-point structure on the free loop spaces makes the derived function algebras – the topological Hochschild homology of the original function algebras – be cyclotomic spectra.

For general super $p$-branes

Double dimensional reduction for the super-$p$-branes in $D$ dimensions which are described by the Green-Schwarz action functional corresponds to moving down and left the diagonals in the brane scan table of consistent such branes:

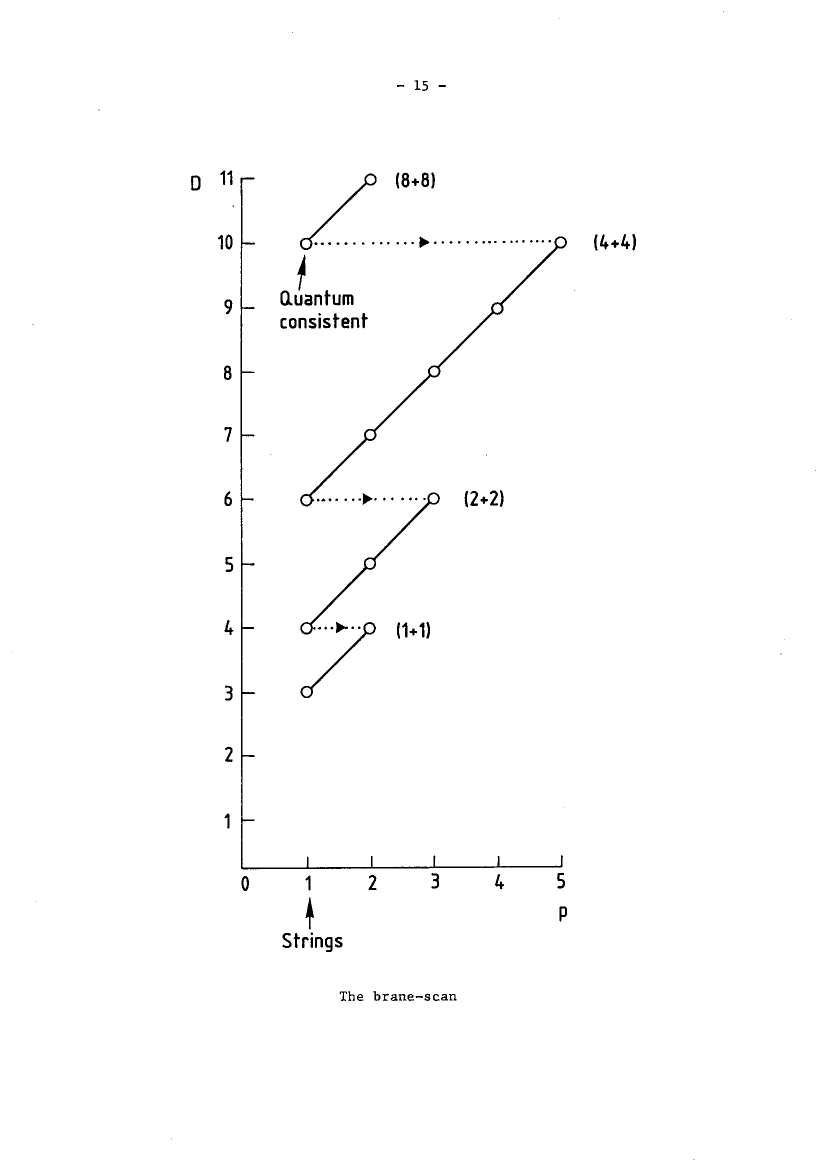
In particular

• the superstring of type IIA string theory appears as the double dimensional reduction of the M2-brane in the KK-compactification from 11-dimensional supergravity/M-theory down to 10-dimensional type II supergravity/type II string theory.

• the D4-brane appears as the double dimensional reduction of the M5-brane under this process;

• the double dimensional reduction of the super 2-brane in 4d is super 1-brane in 3d (see there).

From M-branes to F-branes

• duality between M-theory and type IIA string theory

from M-branes to F-branes: superstrings, D-branes and NS5-branes

M-theory on $S^1_A \times S^1_B$-elliptic fibration	KK-compactification on $S^1_A$	type IIA string theory	T-dual KK-compactification on $S^1_B$	type IIB string theory	geometrize the axio-dilaton	F-theory on elliptically fibered-K3 fibration	duality between F-theory and heterotic string theory	heterotic string theory on elliptic fibration
M2-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	type IIA superstring	$\mapsto$	type IIB superstring	$\mapsto$	“	$\mapsto$	heterotic superstring
M2-brane wrapping $S_B^1$	$\mapsto$	D2-brane	$\mapsto$	D1-brane	$\mapsto$	“
M2-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ strings and $q$ D2-branes	$\mapsto$	(p,q)-string	$\mapsto$	“
M5-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	D4-brane	$\mapsto$	D5-brane	$\mapsto$	“
M5-brane wrapping $S_B^1$	$\mapsto$	NS5-brane	$\mapsto$	NS5-brane	$\mapsto$	“	$\mapsto$	NS5-brane
M5-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ D4-brane and $q$ NS5-branes	$\mapsto$	(p,q)5-brane	$\mapsto$	“
M5-brane wrapping $S_A^1 \times S_B^1$	$\mapsto$		$\mapsto$	D3-brane	$\mapsto$	“
KK-monopole/A-type ADE singularity (degeneration locus of $S^1_A$-circle fibration, Sen limit of $S^1_A \times S^1_B$ elliptic fibration)	$\mapsto$	D6-brane	$\mapsto$	D7-branes	$\mapsto$	A-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 2)		SU-gauge enhancement
KK-monopole orientifold/D-type ADE singularity	$\mapsto$	D6-brane with O6-planes	$\mapsto$	D7-branes with O7-planes	$\mapsto$	D-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 3)		SO-gauge enhancement
exceptional ADE-singularity	$\mapsto$		$\mapsto$		$\mapsto$	exceptional ADE-singularity of elliptic fibration	$\mapsto$	E6-, E7-, E8-gauge enhancement

(e.g. Johnson 97, Blumenhagen 10)

Related concepts

• cyclic loop space, cyclic loop stack

• caloron correspondence

References

General

Formalization of double dimensional reduction via cyclification of classifying spaces/characteristic $L_\infty$-algebras:

in rational homotopy theory:

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Section 3 of T-Duality from super Lie n-algebra cocycles for super p-branes, ATMP Volume 22 (2018) Number 5 (arXiv:1611.06536)

and in full homotopy theory:

• Vincent Braunack-Mayer, Hisham Sati, Urs Schreiber, Section 2.2 of: Gauge enhancement of Super M-Branes via rational parameterized stable homotopy theory, Communications in Mathematical Physics 371: 197 (2019) (arXiv:1806.01115, doi:10.1007/s00220-019-03441-4)

• Hisham Sati, Urs Schreiber: Cyclification of Orbifolds, Comm. Math. Phys. 405 67 (2024) [doi:10.1007/s00220-023-04929-w, arXiv:2212.13836, talk]

Exposition is in

• Urs Schreiber, Section 4 of Super Lie n-algebra of Super p-branes, talks at Fields, Strings, and Geometry Seminar, Surrey, 5th-9th Dec. 2016

and further discussion in

• Luigi Alfonsi, Global Double Field Theory is Higher Kaluza-Klein Theory, Fortsch. d. Phys. 68 3-4 (2020) [arXiv:1912.07089, doi:10.1002/prop.202000010]

• Luigi Alfonsi: The puzzle of global Double Field Theory: open problems and the case for a Higher Kaluza-Klein perspective, Fortschr. Phys. 69 7 (2021) [arXiv:2007.04969, doi:10.1002/prop.202000102]

The case of duality between 11D and 10D IIA supergravity:

• Grigorios Giotopoulos, Hisham Sati: Flux Quantization on 10D Type IIA Superspace via Cyclification from 11D [arXiv:2606.16857]

• Grigorios Giotopoulos, Hisham Sati, Urs Schreiber; §3.2 in: Higher Superspace Supergravity its IR Completions, lecture notes [arXiv:2607.20312]

Reduction of membrane to string

The concept of double dimensional reduction was introduced, for the case of the reduction of the supermembrane in 11d to the Green-Schwarz superstring in 10d, in

• Michael Duff, Paul Howe, T. Inami, Kellogg Stelle, Superstrings in $D=10$ from Supermembranes in $D=11$, Phys. Lett. B191 (1987) 70 and in Michael Duff (ed.) The World in Eleven Dimensions 205-206 (1987) [spire:245249, doi:10.1016/0370-2693(87)91323-2]

The above “brane scan” table showing the double dimensional reduction pattern of the super-$p$-branes given by the Green-Schwarz action functional (see there for more references on this) is taken from

• Michael Duff: Supermembranes: the first fifteen weeks, Class. Quantum Grav. 5 189 (1988) [doi:10.1088/0264-9381/5/1/023]

Reduction of M5-brane to D4-brane

The double dimensional reduction of the M5-brane to the D4-brane:

• Paul Townsend, D-branes from M-branes, Phys. Lett. B 373 (1996) 68–75 [doi:10.1016/0370-2693(96)00104-9, arXiv:hep-th/9512062]

• Mina Aganagic, Jaemo Park, Costin Popescu, John Schwarz, Section 6 of: World-Volume Action of the M Theory Five-Brane, Nucl. Phys. B 496 (1997) 191-214 [arXiv:hep-th/9701166, doi:10.1016/S0550-3213(97)00227-7]

• Mina Aganagic, Jaemo Park, Costin Popescu, John Schwarz, Section 6 of: Dual D-Brane Actions, Nucl. Phys. B 496 (1997) 215-230 [arXiv:hep-th/9702133, doi:10.1016/S0550-3213(97)00257-5]

• Neil Lambert, Constantinos Papageorgakis, Maximilian Schmidt-Sommerfeld, M5-Branes, D4-Branes and Quantum 5D super-Yang-Mills, JHEP 1101:083 (2011) (arXiv:1012.2882)

• Edward Witten, Fivebranes and Knots (arXiv:1101.3216)

• Anajak Phonchantuek, Pichet Vanichchapongjaroen: Double dimensional reduction of M5-brane action in Sen formalism, Eur. Phys. J. C 83 (2023) 721 [arXiv:2305.04861, doi:10.1140/epjc/s10052-023-11892-2]

Reduction of black M2s and black M5s

The differential geometry of the double dimensional reduction of the M2-brane- and M5-brane-charges was maybe first clearly written out in:

• Varghese Mathai, Hisham Sati, §4 in: Some Relations between Twisted K-theory and $E_8$ Gauge Theory, J. High Energ. Phys. 2004 03 (2004) 016 [arXiv:hep-th/0312033, doi:10.1088/1126-6708/2004/03/016]

For their black brane-reductions see:

• José Figueroa-O'Farrill, Joan Simón, Supersymmetric Kaluza-Klein reductions of M2 and M5-branes, Adv. Theor. Math. Phys. 6:703-793, 2003 (arXiv:hep-th/0208107)

Reduction of M-Waves and MK6s

• José Figueroa-O'Farrill, Joan Simón, Supersymmetric Kaluza-Klein reductions of M-waves and MKK-monopoles, Class. Quant. Grav.19:6147-6174, 2002 (arXiv:hep-th/0208108)