nLab Hořava-Witten theory
This entry is about the conjectured relation (duality) between M-theory at MO9-planes and heterotic string theory on these. For the relation of M-theory KK-compactified on a K3-surface and heterotic string theory on a 3-torus see instead at duality between M/F-theory and heterotic string theory.
Context
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
There is an observation by Hořava–Witten 95, Hořava–Witten 96 which suggests that M-theory on an Z/2-orbifold (actually a higher orientifold) of the form is “dual” to heterotic string theory on its boundary (fixed point) “M9-brane”. Therefore one also speaks of “heterotic M-theory” (Ovrut 02).
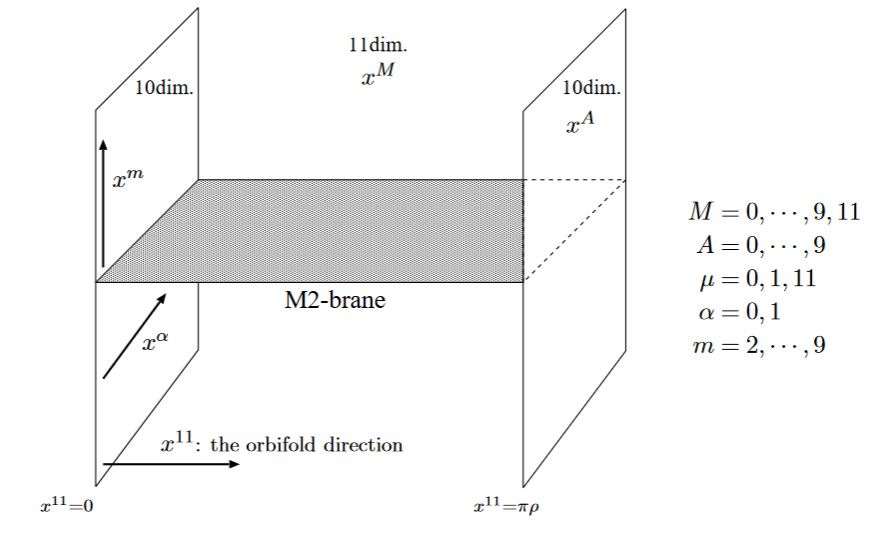
from Kashima 00
In the above the circle factor is taken to be the circle fiber over the 10d type IIA spacetime.
If instead one considers another of the spatial dimensions to be compactified on , then, after T-duality (F-theory) result is supposed to be type I string theory. In this case the intersection of the M2-brane with the M9-brane (the latter now wrapping the M-theory circle fiber) is called the E-string.
More in detail:
One considers the KK-compactification of M-theory on a Z/2-orbifold of a torus, hence of the Cartesian product of two circles
such that the reduction on the first factor corresponds to the duality between M-theory and type IIA string theory, hence so that subsequent T-duality along the second factor yields type IIB string theory (in its F-theory-incarnation). Now the diffeomorphism which exchanges the two circle factors and hence should be a symmetry of M-theory is interpreted as S-duality in type II string theory:

graphics taken from Horava-Witten 95, p. 15
If one considers this situation additionally with a -orbifold quotient of the first circle factor, one obtains the duality between M-theory and heterotic string theory (Horava-Witten theory). If instead one performs it on the second circle factor, one obtains type I string theory.
Here in both cases the involution action is by reflection of the circle at a line through its center. Hence if we identify then the action is by multiplication by /1 on the real line.
In summary:
M-theory on
-
yields heterotic string theory
-
yields type I' string theory
Hence the S-duality that swaps the two circle factors corresponds to a duality between heterotic E and type I’ string theory. And T-dualizing turns this into a duality between type I and heterotic string theory.

graphics taken from Horava-Witten 95, p. 16
Duality between M-theory and heterotic string theory
Here each of the two copies of the heterotic gauge theory is a “hidden sector” with respect to the other.
The orbifold equivariance condition of the supergravity C-field is that discussed at orientifold (there for the B-field). Therefore it has to vanish at the two fixed fixed points of the -action. Thereby the quantization condition
on the supergravity C-field becomes the condition for the Green-Schwarz mechanism of the heterotic string theory on the “boundary” (the orbifold fixed points).
Duality between M-theory and type I string theory
duality between M-theory and type I string theory
originally suggested in (Horava-Witten 95, section 3)
Further evidence is reviewed in APT 98
Duality between heterotic and type I string theory
duality between heterotic and type I string theory
via S-duality in the F-theory-picture…
Related concepts
Properties
Boundary conditions
The supergravity C-field is supposed to vanish, and differentially vanish at the boundary in the HW model, meaning that also the local connection 3-form vanishes there. The argument is roughly as follows (similar for as in Falkowski, section 3.1).
in the Lagrangian of 11-dimensional supergravity is supposed to be well-defined on fields on the orbifold and hence is to be -invariant.
Let be the canonical vector field along the circle factor. Then the component of which is annihilated by the contraction is necessarily even, so the component is also even. It follows that also is even.
Moreover, the kinetic term
is to be invariant. With the above this now implies that the components of annihiliated by is odd, because so is the mixed component of the metric tensor.
This finally implies that the restriction of to the orbifold fixed points has to be closed.
Related concepts
References
General
The original articles are
-
Petr Hořava, Edward Witten, Heterotic and Type I string dynamics from eleven dimensions, Nucl. Phys. B 460 (1996) 506 [arXiv:hep-th/9510209, doi:10.1016/0550-3213(95)00621-4]
-
Edward Witten, Strong Coupling Expansion Of Calabi-Yau Compactification, Nucl. Phys.B 471:135-158, 1996 (arXiv:hep-th/9602070)
-
Petr Hořava, Edward Witten, Eleven dimensional supergravity on a manifold with boundary, Nucl. Phys. B475 (1996) 94 (arXiv:hep-th/9603142)
Review is in
-
Piyush Kumar, Hořava-Witten theory (2004) (pdf)
-
Paul Townsend, Four Lectures on M-Theory (arXiv:hep-th/9612121).
-
Burt Ovrut, Lectures on Heterotic M-Theory, in Strings, Branes and Extra Dimensions, TASI 2001, World Scientific (2004) 359-407 [arXiv:hep-th/0201032, doi:10.1142/9789812702821_0007]
-
Adam Falkowski, section 3 of Five dimensional locally supersymmetric theories with branes, Master Thesis, Warsaw (pdf)
The black M2-brane solution in HW-theory, supposedly yielding the black heterotic string at the intersection with the M9-brane is discussed in
-
Zygmunt Lalak, André Lukas, Burt Ovrut, Soliton Solutions of M-theory on an Orbifold, Phys. Lett. B425 (1998) 59-70 (arXiv:hep-th/9709214)
-
Ken Kashima, The M2-brane Solution of Heterotic M-theory with the Gauss-Bonnet terms, Prog.Theor.Phys. 105 (2001) 301-321 (arXiv:hep-th/0010286)
More on the Green-Schwarz mechanism in Hořava-Witten theory:
-
E. Dudas, J. Mourad, On the strongly coupled heterotic string, Phys. Lett. B400 (1997) 71-79 (arXiv:hep-th/9701048)
-
Adel Bilal, Jean-Pierre Derendinger, Roger Sauser, M-Theory on : New Facts from a Careful Analysis, Nucl. Phys. B576 (2000) 347-374 (arXiv:hep-th/9912150)
-
Ian G Moss, A new look at anomaly cancellation in heterotic M-theory, Phys. Lett. B637 (2006) 93-96 (arXiv:hep-th/0508227)
-
Sergio Lukic, Gregory Moore, Flux corrections to anomaly cancellation in M-theory on a manifold with boundary (arXiv:hep-th/0702160)
-
Ian G Moss, Higher order terms in an improved heterotic M theory, JHEP 0811:067, 2008 (arXiv:0810.1662)
-
Fei Han, Kefeng Liu, Weiping Zhang, Anomaly Cancellation and Modularity. II: case, Sci. China Math. 60, 985–994 (2017) (arXiv:1209.4540, doi:10.1007/s11425-016-9034-1)
Explicit discussion of worldvolume CFT of the M2-branes ending on the HW fixed points and becoming heterotic strings is discussed, via the BLG model, in
- Neil Lambert, Heterotic M2-branes, Physics Letters B Volume 749, 7 October 2015, Pages 363–367 (arXiv:1507.07931)
After KK-reduction to 5d supergravity there is a corresponding 5d mechanism, see the references there.
Discussion of the duality between heterotic and type I string theory includes
- I. Antoniadis, H. Partouche, T.R. Taylor, Lectures on Heterotic-Type I Duality, Nucl.Phys.Proc.Suppl. 61A (1998) 58-71; Nucl.Phys.Proc.Suppl. 67 (1998) 3-1
Discussion of string phenomenology in Horava-Witten theory:
- Burt Ovrut, Vacuum Constraints for Realistic Heterotic M-Theories, Symmetry 2018, 10(12), 723 (arXiv:1811.08892, doi:10.3390/sym10120723)
Phenomenology
Discussion of phenomenology/string phenomenology for the heterotic M-theory, relating to the standard model of particle physics:
-
Ron Donagi, Burt Ovrut, Tony Pantev, Daniel Waldram, Standard Models from Heterotic M-theory, Adv. Theor. Math. Phys. 5 (2002) 93-137 (arXiv:hep-th/9912208)
-
Ron Donagi, Burt Ovrut, Tony Pantev, Daniel Waldram, Standard Model Vacua in Heterotic M-Theory, talk at Strings ‘99, Potsdam, Germany, 19 - 24 Jul 1999 (arXiv:hep-th/0001101)
and with emphasis on heterotic line bundle-models:
- Sebastian Dumitru, The strongly coupled heterotic string: Geometry & Phenomenology [arXiv:2206.12310, spire:2100628]
See also:
- Cédric Deffayet, Burt Ovrut, Paul Steinhardt, Stable Vacua with Realistic Phenomenology and Cosmology in Heterotic M-theory Satisfying Swampland Conjectures [arXiv:2401.04828]
Gaugino condensation and supersymmetry breaking
Discussion of gaugino condensation and supersymmetry breaking in Horava-Witten theory, where the two heterotic MO9-branes provide a natural mechanism for supersymmetry breaking on one (the physical brane) by gaugino condensation on the other (the “dark sector” brane):
lecture notes:
- Hans-Peter Nilles, Gaugino Condensation and SUSY Breakdown, Lectures at Cargese School of Physics and Cosmology, Cargese, France, August 2003 (arXiv:hep-th/0402022)
original articles:
-
I. Antoniadis, M. Quiros, On the M-theory description of gaugino condensation, Phys.Lett. B416 (1998) 327-333 (arXiv:hep-th/9707208)
-
I. Antoniadis, M. Quiros, Supersymmetry breaking in M-theory and gaugino condensation, Nucl.Phys. B505 (1997) 109-122 (arXiv:hep-th/9705037)
-
André Lukas, Burt Ovrut, Daniel Waldram, Gaugino condensation in M theory on , Phys. Rev. D 57, 7529 (1998) (arXiv:hep-th/9711197, doi:10.1103/PhysRevD.57.7529)
-
André Lukas, Burt Ovrut, Daniel Waldram, Five-Branes and Supersymmetry Breaking in M-Theory, JHEP 9904:009, 1999 (arXiv:hep-th/9901017)
specifically for M-theory on S1/G_HW times H/G_ADE:
- Zygmunt Lalak, Steven Thomas, Gaugino Condensation, Moduli Potentials and Supersymmetry Breaking in M-Theory Models, Nuclear Physics B Volume 515, Issues 1–2, 30 March 1998, Pages 55-72 Nuclear Physics B (hep-th/9707223, doi:10.1016/S0550-3213(97)00784-0)
With emphasis on heterotic line bundles in the hidden sector:
-
Anthony Ashmore, Sebastian Dumitru, Burt Ovrut, Section 4.2 of: Line Bundle Hidden Sectors for Strongly Coupled Heterotic Standard Models (arXiv:2003.05455)
-
Anthony Ashmore, Sebastian Dumitru, Burt Ovrut, Explicit Soft Supersymmetry Breaking in the Heterotic M-Theory B−L MSSM (arXiv:2012.11029)
Generalization to M-theory on
Generalization to M-theory on S1/G_HW times H/G_ADE:
-
Zygmunt Lalak, Steven Thomas, Gaugino Condensation, Moduli Potentials and Supersymmetry Breaking in M-Theory Models (hep-th/9707223)
-
V. Kaplunovsky, Jacob Sonnenschein,Stefan Theisen, S. Yankielowicz, On the Duality between Perturbative Heterotic Orbifolds and M-Theory on (arXiv:hep-th/9912144)
-
E. Gorbatov, V.S. Kaplunovsky, J. Sonnenschein, Stefan Theisen, S. Yankielowicz, On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015, 2002 (arXiv:hep-th/0108135)
-
Davide Gaiotto, Alessandro Tomasiello, Holography for theories in six dimensions, JHEP12(2014)003 (arXiv:1404.0711)
-
Michele Del Zotto, Jonathan Heckman, Alessandro Tomasiello, Cumrun Vafa, Section 6 of: 6d Conformal Matter, JHEP02(2015)054 (arXiv:1407.6359)
-
John Huerta, Hisham Sati, Urs Schreiber, Example 2.2.7 of: Real ADE-equivariant (co)homotopy and Super M-branes, CMP (2019) (arXiv:1805.05987, doi:10.1007/s00220-019-03442-3)
For 7d supergravity
Discussion for 7d supergravity:
-
Tony Gherghetta, Alex Kehagias, Anomaly Cancellation in Seven-Dimensional Supergravity with a Boundary, Phys.Rev. D68 (2003), 065019, (arXiv:hep-th/0212060)
-
Spyros D. Avramis, Alex Kehagias, Gauged Supergravity on the Orbifold (arXiv:hep-th/0407221)
-
T.G. Pugh, Ergin Sezgin, Kellogg Stelle, / Heterotic Supergravity with Gauged R-Symmetry (arXiv:1008.0726)
Last revised on February 14, 2024 at 08:02:41. See the history of this page for a list of all contributions to it.