nLab landscape of string theory vacua

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Contents

Context

Vacua

String theory

Ingredients

Critical string models

Extended objects

Topological strings

Backgrounds

Phenomenology

Contents

Idea

recalling the context

The undertaking called string theory started out as perturbative string theory where the idea was to encode spacetime physics in perturbation theory by an S-matrix that is obtained by a sum of the integrals of the correlators of a fixed 2d superconformal field theory over the moduli spaces of conformal structures on surfaces of all possible genera – thought of as the second quantization of a string sigma-model.

The S-matrix elements obtained this way from the string perturbation series could be seen to be approximated by an ordinary effective QFT (some flavor of supergravity coupled to gauge theory and fermions) on target space.

(The first superstring revolution was given by the realization that this makes sense: the effective background theories obtained this way are indeed free of quantum anomalies.)

Hence it is the choice of worldsheet 2d SCFT which in perturbative string theory translates products of “field insertions” into scattering amplitudes. In perturbative AQFT it is the choice of vacuum state which does this, and therefore 2d SCFTs are the perturbative string theory vacua.

narrowing in on the issue

The second superstring revolution was given by the realization that all these background field theories seem to fit into one single bigger context that seems to exists independently of their perturbative definitions.

Aspects of this bigger non-perturbative context are known as M-theory. While one couldn’t figure out what that actually is, the circumstantial evidence suggested that whatever it is, it has a low-energy limit where it also looks like an effective background field theory, this time 11-dimensional supergravity.

In a different but similar manner, other background field theories were found whose classical solutions are thought to encode “stable solutions” (“vacuum solutions”) of whatever physical theory this non-perturbative definition of string theory is.

Here, when talking about a “stable solution” one thinks of solutions of these theories of gravity with plenty of extra fields that look like Minkowski space times something else, such that all these extra fields are constant in time (using the simple Minkowsi-space-times-internal-part-ansatz to say what “constant in time” means), hence sitting at the bottom of their corresponding effective potentials.

Solutions with this property, in particular for all the scalar fields that appear, are said to have stabilized moduli : the scalar fields that encode various properties of the geometry of the solution are constant in time.

Since these geometric properties determine, in the fashion of Kaluza-Klein theory, the effective physics in the remaining Minkowski space factor, it is these “moduli-stabilized” solutions that have a first chance of being candidate solutions of whatever that theory is we are talking about, which describe the real world.

the landscape

At some point there had been the hope that only very few such solutions exist. When arguments were put forward that this is far from being true, the term landscape for the collection of all such solutions was invented.

So, to summarize in a few words, the landscape of string theory vacua is…

Flux compactifications

One widely studied class of moduli-stabilized solutions to the string-theory background equations is that of flux compactifications.

These are classical solutions to the corresponding supergravity theory that are of the form M 4×CYM^4 \times CY with CYCY some Calabi-Yau manifold of six real dimensions such that the RR-field in the solution has nontrivial values on CYCY. Its components are called the fluxes .

The presence of this RR-field in the solution induces an effective potential for the scalar moduli fields that parameterize the geometry of CY. Hence by choosing the RR-field suitably one can find classical solutions in which all these moduli have values that are constant in time.

A review of flux compactifications is for instance in (Graña 05)

Computer scans of Gepner model compactifications

Discussion of string phenomenology of intersecting D-brane models KK-compactified with non-geometric fibers such that the would-be string sigma-models with these target spaces are in fact Gepner models (in the sense of Spectral Standard Model and String Compactifications) is in (Dijkstra-Huiszoon-Schellekens 04a, Dijkstra-Huiszoon-Schellekens 04b):

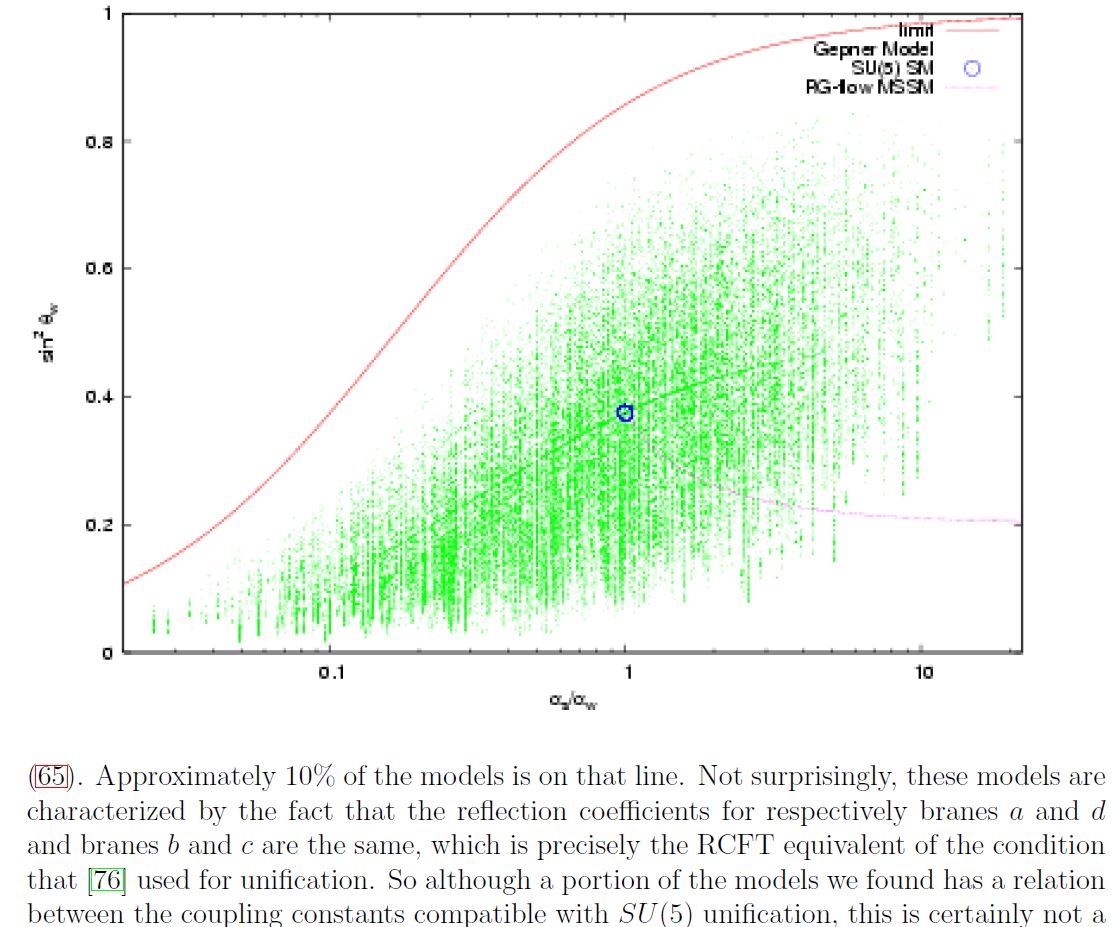
A plot of standard model-like coupling constants in a computer scan of Gepner model-KK-compactification of intersecting D-brane models according to Dijkstra-Huiszoon-Schellekens 04b.

The blue dot indicates the couplings in SU(5)SU(5)-GUT theory. The faint lines are NOT drawn by hand, but reflect increased density of Gepner models as seen by the computer scan.

at least one thing missing in the discussion here is the subtlety explained out by Jacques Distler in blog discussion here

References

F-theory flux compactification

Surveys of the general story of flux compactification in F-theory includes

Landscape of Type II vacua

Scan of the moduli space of semi-realistic type IIB intersecting D-brane model KK-compactifications on orbifolds of Gepner models is in

and scan type IIB intersecting D-brane model KK-compactifications on toroidal orbifolds is in

Landscape of heterotic vacua

The origin of all string phenomenology is the top-down approach in the heterotic string due to (Candelas-Horowitz-Strominger-Witten 85).

A brief review of motivations for GUT models in heterotic string theory is in

The following articles establish the existences of exact realization of the gauge group and matter-content of the MSSM in heterotic string theory (not yet checking Yukawa couplings):

A computer search through the “landscape” of Calabi-Yau varieties showed severeal hundreds more such exact heterotic standard models (about one billionth of all CYs searched, and most of them arising as SU(5)SU(5)-GUTs)

The resulting database of compactifications is here:

Review includes

Computation of metrics on these Calabi-Yau compactifications (eventually needed for computing their induced Yukawa couplings) is started in

This “heterotic standard model” has a “hidden sector” copy of the actual standard model, more details of which are discussed here:

The issue of moduli stabilization in these kinds of models is discussed in

Principles singling out heterotic models with three generations of fundamental particles are discussed in:

See also

Moduli space of 2d SCFTs

Some general thoughts on what a moduli space of 2d CFTs should be are in

The compactness results mentioned there are discussed in

based on conjectures in

Phenomenological speculation

Early and technical articles that amplified the existence of a finite but very large number of string theory compactifications are

which says on p. 2

Although the consistency requirements which string theories have to satisfy are quite restrictive, it has become clear that there are more solutions than one originally expected. [] Although the possibility of making Lorentz rotations suggests a continuous infinity of new ten dimensional theories, there is actually only a discrete set of theories that makes physical sense, as we will explain below.

and

which says in conclusion on page 45-46

Although the number of chiral theories of this type is finite, our results suggest that there exist very many of them, so that a complete enumeration appears impossible.

A popular account of these observations was given in

a commented translation of which later appeared as

Similarly

The articles Lerche-Lüst-Schellekens 86, Lerche-Lüst-Schellekens 87, and the speech Schellekens 98, did not cause much of excitement then. Also they did not discuss moduli stabilization, which could still have been thought to reduce the number of vacua. Excitement was only later caused instead by more vague discussion of flux compactification vacua with moduli stabilization in type IIB string theory:

That there are 10 hundreds10^{hundreds} different flux compactifications was maybe first said explicitly in

The idea became popular in discussion of the cosmological constant with the alleged construction of a large set of metastable de Sitter spacetime-vacua in

and the amplification of the complication of the KKLT 03-construction its alleged vastness in

Review includes

(Beware that the approach of KKLT 03 is argued to be false in DanielssonVanRiet 18 and is being abandoned in Obied-Ooguri-Spodyneiko-Vafa 18, Danielsson et. al 18).

The specific (but arbitrary) value “10 50010^{500}” for the typical number of flux compactification, which became iconic in public discussion of the issue, originates in

Previously

had considered 10 12010^{120} and earlier Lerche-Lüst-Schellekens 87 had 10 150010^{1500}.

A review of the issue of flux compactifications is in

General considerations on this state of affairs are in

The fact that in principle all the parameters of the “landscape” of string theory vacua are dynamical (are moduli fields) and the idea that an eternal cosmic inflation might be something like an ergodic process in this landscape has led to ideas to connect this to phenomenology and the standard model of cosmology/standard model of particle physics by way of statistical mechanics.

Summaries of this line of thinking include

  • Raphael Bousso, The State of the Multiverse:

    The String Landscape, the Cosmological Constant, and the Arrow of Time_, 2011 (pdf)

For more on this see the references at multiverse and eternal inflation.

Landscape of de Sitter vacua (or not)

On the other hand, discussion casting doubt on the existence of a large number of de Sitter spacetime perturbative string theory vacua includes the following:

  • Tom Banks, Landskepticism: or Why Effective Potentials Don’t Count String Models (arXiv:hep-th/0412129)

  • Tom Banks, The Top 10 50010^{500} Reasons Not to Believe in the Landscape (arXiv:1208.5715)

  • Tom Banks, On the Limits of Effective Quantum Field Theory: Eternal Inflation, Landscapes, and Other Mythical Beasts (arxiv:1910.12817)

    from pages 14-22:

    these considerations lead to conclusions at odds with the seemingly similar arguments of [[ the swampland conjectures ]]. [⋯][\cdots] Perturbative moduli space completely distorts the true nature of the class of consistent models.

    It’s important to realize that the entire procedure just outlined for finding (meta) stable AdS minima of a non-perturbative effective potential is purely hypothetical and has no basis in well founded string theory calculations. [⋯].[\cdots].

    The hypothesis of the String Landscape is entirely based on low energy effective field theory ideas about finding “vacua” by minimizing an effective potential. Everything that’s been said above indicates that this idea has no validity in genuine models of quantum gravity. [⋯][\cdots]

    The most serious issue, in my opinion, is the contention that one can make the AdS radius much larger thanthe size of the compact manifold. All well established examples of large radius AdS/CFT havea compact manifold of dimension 2 or greater whose radius is comparable to that of the AdSspace. In Appendix A we’ll present an argument based on the properties of AdS black holes,that this is in fact necessary.

    The next step in the construction of “realistic” models involves “adding an anti-brane to break supersymmetry and make the c.c. positive”. This is supposed to be a small modification of the model, calculable in low energy effective field theory, and that seems manifestly incorrect. [⋯][\cdots].

    even if one believes that the construction of meta-stable dS models is reliable, there is no clear argument about what the proper observables of the model are nor that different dS constructions are part of the same model. Neither is there an interpretation of these correlators as transition amplitudes in a quantum mechanical model. [⋯][\cdots]

    The conclusion that effective field theorists should draw from this is that unlike super-symmetric string models in flat or AdS space-time, many of which have at least perturbative definitions as mathematical models obeying the axioms of quantum mechanics, all literature on the String Landscape is speculation based on the unfounded notion that all string models with a given amount of SUSY are part of one single model and that it makes sense to define an effective action that encompasses all string models. Every single non-perturbative construction of string models contradicts this claim [⋯][\cdots]

  • Brennan-Carta-Vafa 17

  • David Kutasov, Travis Maxfield, Ilarion Melnikov, Savdeep Sethi, Constraining de Sitter Space in String Theory, Phys. Rev. Lett. 115, 071305 (2015) (arXiv:1504.00056)

  • Jakob Moritz, Ander Retolaza, Alexander Westphal, Towards de Sitter from 10D, Phys. Rev. D 97, 046010 (2018) (arXiv:1707.08678)

  • Savdeep Sethi, Supersymmetry Breaking by Fluxes (arXiv:1709.03554)

    re-amplified in:

    Savdeep Sethi, Hope or No Hope for a String Landscape?, talk at StringPheno2019 (pdf, pdf)

  • Ulf Danielsson, Thomas Van Riet, What if string theory has no de Sitter vacua?, International Journal of Modern Physics D, Vol. 27, No. 12, 1830007 (2018) (arXiv:1804.01120, doi:10.1142/S0218271818300070)

  • Thomas Van Riet, Is dS space in the Swampland, talk at StringPheno18 (pdf slides)

  • Thomas Van Riet, Status of KKLT, talk at Simons summer workshop 2018 (recording)

  • Jakob Moritz, Ander Retolaza, Alexander Westphal, On uplifts by warped anti-D3-branes (arXiv:1809.06618)

The Swampland

Discussion of aspects of effective field theories which might rule them out as having a UV-completion by a string theory vacuum (be in the “swampland”) has been initiated in

Comprehensive review is in:

  • Eran Palti, The Swampland: Introduction and Review, lecture notes (arXiv:1903.06239)

See also

Implications of the possible non-existence of de Sitter vacua in string theory are explored in

Last revised on March 18, 2020 at 08:47:08. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (68 revisions) Cite Print Source