nLab swampland
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
- Idea
- Swampland conjectures
- No global symmetries conjecture
- Completeness hypothesis
- BPS completeness hypothesis
- Weak gravity conjecture
- Electric weak gravity conjecture
- Magnetic weak gravity conjecture
- Convex hull weak gravity conjecture
- Sublattice (or tower) weak gravity conjecture
- Swampland distance conjecture
- Emergent string conjecture
- AdS distance conjecture
- AdS instability conjecture
- dS conjecture
- Trans-planckian censorship conjecture
- Asymptotic dS conjecture
- Swampland cobordism conjecture
- References
Idea
In string theory the term swampland had been introduced (Vafa 05) to publicly highlight the basic fact that many effective quantum field theory vacua will not admit a UV-completion to a string theory vacuum, hence that admitting a completion to a string theory vacuum is a strong constraint, hence that string theory predicts many more conditions to be satisfied by gauge groups, field content and coupling constants than predicted by plain quantum field theory.
The terminology was motivated since the collection of string theory vacua had previously come to be called the landscape of string theory vacua. The idea is to imagine the remaining EFTs not “in” this landscape to form a space “away from the landscape”, whence the colorful imagery of a swampland.
More in detail, there is supposedly a map
that takes string theory vacua to their low-energy approximation by vacua of effective quantum field theories. One way to possibly formalize this is to take the point-particle limit (ppl) of 2d SCFTs to obtain spectral triples (as discussed at 2-spectral triple) taking string worldsheets to Feynman diagrams:
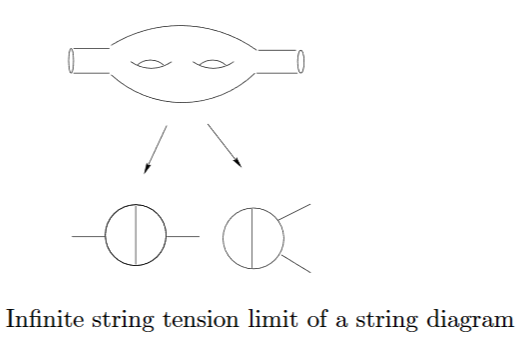
graphics grabbed from Schubert 96
Then with language of homological algebra or more generally of category theory we may begin to formalize the situation as follows:
-
the domain of (1) is the landscape of string theory vacua;
-
the image of (1) is the landscape of corresponding eQFTs that admit stringy UV-completion;
-
the kernel of (1), or more generally its fiber over any EFT, is the space of different choices of stringy UV-completion of the same effective quantum field theory.
Making this fully precise requires saying more about what the domain and codomain in (1) actually are, and in which ambient category (they will be some kind of moduli stacks in an ambient (∞,1)-category which may not quite be stable, whence “cokernel” may need to be interpreted in a non-abelian sense; but such details don’t change the general idea here).
For example, part of what it means to specify a string theory vacuum is to declare the D-brane charge contained in this vacuum (subject to RR-field tadpole cancellation against O-plane-charges). In actual string theory this RR-field charge is supposed to be (see there) a cocycle in some flavour of topological K-theory (twisted equivariant differential KR-theory), while its image in the underlying effective field theory is in the corresponding flavour of ordinary cohomology/de Rham cohomology. The map that relates the two incarnations of RR-field charge is the Chern character, which is what formalizes the map (1) in in the D-brane charge “sector” of the theory
The Chern character in general does have non-trivial cokernel (“swampland RR-fields”) and kernel (choices of UV-completion of the effective RR-fields). In fact it fits not just in a short exact sequence, but in the differential cohomology hexagon (see there for more) of K-theory.
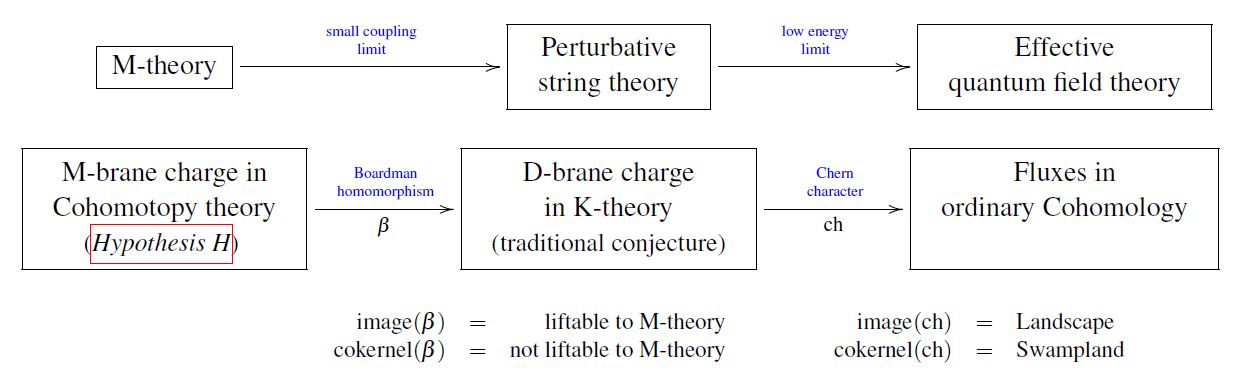
graphics grabbed from SS 18
In contrast to this example, the literature on the “swampland” phenomenon is currently dominated by informal hand-wavy arguments. Starting with Ooguri-Vafa 06 is an attempt to guess semi-precise rules-of-thumb for recognizing EFTs in the swampland, now known as the swampland conjectures. Motivated by the re-opening of the question whether de Sitter spacetime actually appears in string theory vacua or not (Danielsson-van Riet 18), these swampland conjecture currently revolve around bounds on the cosmological constant in relation to scalar fields in the theory.
An argument that much of the existing swampland literature does not even live up to the level of rigour of folklore string theory, and in fact that it is fundamentally flawed, is made in Banks 19.
Swampland conjectures
The following list of statements have come (around 2020-2021) to be widely discussed in a sector of the string phenomenology community which associates with the “swampland” imagery. They are now commonly referred to and known as “conjectures”, specifically “the swampland conjectures”, but the terms used tend to remain vague/undefined and may change their intended meaning with context (not the least the notion of “state in quantum gravity”, which however in most of these statements really means: classical solitonic black brane-solution in some supergravity-theory – e.g. in Conj. ).
But some of these statements have been interpreted in special cases as more precise statements about moduli spaces of Calabi-Yau manifolds, and in this form they may be closer to conjectures in the sense of established sense of mathematics.
No global symmetries conjecture
Conjecture
A theory coupled to gravity must have no global symmetries, which means that they are either broken or gauged.
This includes global -form symmetries as well as global discrete symmetries.
Completeness hypothesis
Conjecture
A gauge theory coupled to gravity must contain physical states with all possible gauge charges consistent with Dirac charge quantization.
Remark
This immediately implies that any continuous gauge group (i.e. a Lie group) must be compact. However, this does not restrict discrete gauge groups, which can be non-compact (e.g. duality groups).
BPS completeness hypothesis
Conjecture
If a given charge can be populated by BPS states, then the physical spectrum must contain a BPS state with this charge.
Weak gravity conjecture
Electric weak gravity conjecture
Conjecture
Given a -gauge theory weakly coupled to gravity with gauge coupling , there must exist an electrically charged state with mass and charge satisfying
where is the Planck mass.
The electric weak gravity conjecture can be also formulated by stating that there must exist an electrically charged state satisfying
where is the non-quantized charge, and are charge and mass of an extremal black hole.
Magnetic weak gravity conjecture
Conjecture
Given a -gauge theory weakly coupled to gravity with gauge coupling , The cutoff scale of the effective field theory must be bounded from above by the gauge coupling as
where is the Planck mass and is the dimension.
Convex hull weak gravity conjecture
Conjecture
Given a -gauge theory weakly coupled to gravity, let be the charge to mass ratio of a charged state and let be the set of charged states in the theory. Then, the convex set of the set must contain the unit ball as measured by the kinetic matrix of the -gauge theory.
This condition is a stronger statement than requiring the weak gravity conjecture to be satised for each -gauge theory.
Sublattice (or tower) weak gravity conjecture
(…)
Swampland distance conjecture
Terminology
Consider the moduli space of a theory coupled to gravity, which is parametrized by the expectation values of some field that has no potential. Starting from any point there always exists another point such that their geodesic distance? is infinite. This is called infinite field distance limit.
Example
The decompactification limit in compactified string theory is the standard example of infinite field distance limit.
Conjecture
There exists an infinite tower of states with a mass scale that becomes exponentially light at any infinite field distance limit as
where is a positive constant.
Emergent string conjecture
Conjecture
Any infinite field distance limit is either
-
a decompactification limit, or
-
a limit in which a weakly coupled string becomes tensionless.
This is a refinement of the swampland distance conjecture which explicits the nature of the tower of states.
AdS distance conjecture
Conjecture
Any AdS vacuum has an infinite tower of states that becomes light in the flat spacetime limit , satisfying
where is a constant.
AdS instability conjecture
Conjecture
Any non-supersymmetric vacuum? is at best metastable (and eventually has to decay).
dS conjecture
Conjecture
The scalar potential of an effective field theory weakly coupled to gravity must satisfy the following bound on its derivatives:
where is positive.
The dS conjecture was further refined as it follows.
Conjecture
The previous bound needs to be imposed only if the condition
for some , on the second derivative of the potential is violated.
Thanks to this refinement, only proper dS minima are excluded and not general critical points.
Trans-planckian censorship conjecture
(…)
Asymptotic dS conjecture
Conjecture
The scalar potential of an effective field theory weakly coupled to gravity presents a runaway behavior when approaching an infinite field distance point, i.e.
where .
This is an asymptotic version of the dS conjecture.
Swampland cobordism conjecture
From McNamara & Vafa 2019:
Conjecture
For any quantum gravity theory compactified on a -dimensional internal manifold, some kind of “quantum-gravity version” of a cobordism group must vanish in degree . In heuristic symbols:
Remark
A rigorous discussion of a possible role of cobordism cohomology in M-theory, assuming Hypothesis H, is in Sati & Schreiber 21a; for relation to discussion of Conj. see p. 83 there.
References
General
The terminology “swampland”, in the context of string phenomenology, originates with:
- Cumrun Vafa, The String Landscape and the Swampland (arXiv:hepth/0509212)
Review and lecture notes:
-
Eran Palti, The Swampland: Introduction and Review, lecture notes (arXiv:1903.06239)
-
Marieke van Beest, José Calderón-Infante, Delaram Mirfendereski, Irene Valenzuela, Lectures on the Swampland Program in String Compactifications (arXiv:2102.01111)
Further discussion:
-
Hirosi Ooguri, Cumrun Vafa, On the Geometry of the String Landscape and the Swampland, Nucl.Phys.B766:21-33, 2007 (arXiv:hep-th/0605264)
-
T. Daniel Brennan, Federico Carta, Cumrun Vafa, The String Landscape, the Swampland, and the Missing Corner (arXiv:1711.00864)
-
Ben Heidenreich, Matthew Reece, Tom Rudelius, Emergence and the Swampland Conjectures (arXiv:1802.08698)
-
Hee-Cheol Kim, Houri-Christina Tarazi, Cumrun Vafa, Four Dimensional SYM and the Swampland (arXiv:1912.06144)
See also
- Wikipedia, Swampland_(physics)
Beware that the landscape literature is presently dominated by non-rigorous hand-wavy string phenomenology:
-
Tom Banks, On the Limits of Effective Quantum Field Theory: Eternal Inflation, Landscapes, and Other Mythical Beasts (arxiv:1910.12817)
from pages 14-22:
these considerations lead to conclusions at odds with the seemingly similar arguments of [the swampland conjectures]. Perturbative moduli space completely distorts the true nature of the class of consistent models.
It’s important to realize that the entire procedure just outlined for finding (meta) stable AdS minima of a non-perturbative effective potential is purely hypothetical and has no basis in well founded string theory calculations.
The hypothesis of the String Landscape is entirely based on low energy effective field theory ideas about finding “vacua” by minimizing an effective potential. Everything that’s been said above indicates that this idea has no validity in genuine models of quantum gravity.
The most serious issue, in my opinion, is the contention that one can make the AdS radius much larger thanthe size of the compact manifold. All well established examples of large radius AdS/CFT havea compact manifold of dimension 2 or greater whose radius is comparable to that of the AdSspace. In Appendix A we’ll present an argument based on the properties of AdS black holes,that this is in fact necessary.
The next step in the construction of “realistic” models involves “adding an anti-brane to break supersymmetry and make the c.c. positive”. This is supposed to be a small modification of the model, calculable in low energy effective field theory, and that seems manifestly incorrect. .
even if one believes that the construction of meta-stable dS models is reliable, there is no clear argument about what the proper observables of the model are nor that different dS constructions are part of the same model. Neither is there an interpretation of these correlators as transition amplitudes in a quantum mechanical model.
The conclusion that effective field theorists should draw from this is that unlike super-symmetric string models in flat or AdS space-time, many of which have at least perturbative definitions as mathematical models obeying the axioms of quantum mechanics, all literature on the String Landscape is speculation based on the unfounded notion that all string models with a given amount of SUSY are part of one single model and that it makes sense to define an effective action that encompasses all string models. Every single non-perturbative construction of string models contradicts this claim
Identification of the swampland charge structure with the cokernel of the Chern character:
- Hisham Sati, Urs Schreiber, Lift of fractional D-brane charge to equivariant Cohomotopy theory (arXiv:1812.09679, Python code)
de Sitter vacua
On the question whether de Sitter spacetime-vacua belong to the swampland or not:
-
Ulf Danielsson, Thomas Van Riet, What if string theory has no de Sitter vacua?, International Journal of Modern Physics D, Vol. 27, No. 12, 1830007 (2018) (arXiv:1804.01120, doi:10.1142/S0218271818300070)
-
Thomas Van Riet, Is dS space in the Swampland, talk at StringPheno18 (pdf slides)
-
Thomas Van Riet, Status of KKLT, talk at Simons summer workshop 2018 (recording)
-
Georges Obied, Hirosi Ooguri, Lev Spodyneiko, Cumrun Vafa, De Sitter Space and the Swampland (arXiv:1806.08362)
-
Prateek Agrawal, Georges Obied, Paul Steinhardt, Cumrun Vafa, On the Cosmological Implications of the String Swampland (arXiv:1806.09718)
-
Cumrun Vafa, Cosmology and the String Swampland, talk at Strings 2018 (pdf slides, recording)
-
Frederik Denef, Arthur Hebecker, Timm Wrase, The dS swampland conjecture and the Higgs potential (arXiv:1807.06581)
-
Ulf Danielsson, The quantum swampland (arXiv:1809.04512)
(argues that the issue with stringy de Sitter moduli stabilization raised in Sethi 17 is related to the de Sitter instability seen in QFT, according to the references above)
-
Georges Obied, Hirosi Ooguri, Lev Spodyneiko, Cumrun Vafa, De Sitter Space and the Swampland (arXiv:1806.08362)
-
Jakob Moritz, Ander Retolaza, Alexander Westphal, On uplifts by warped anti-D3-branes (arXiv:1809.06618)
-
Iosif Bena, Emilian Dudas, Mariana Graña, Severin Lüst, Uplifting Runaways (arXiv:1809.06861)
-
Clay Cordova, G. Bruno De Luca, Alessandro Tomasiello, Classical de Sitter Solutions of Ten-Dimensional Supergravity [arXiv:1812.04147]
On de Sitter spacetime cosmology realized in brane world models in ambient AdS-bulk spacetime:
-
Souvik Banerjee, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Marjorie Schillo, Emergent de Sitter cosmology from decaying AdS (arXiv:1807.01570)
-
Souvik Banerjee, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Marjorie Schillo, de Sitter Cosmology on an expanding bubble (arXiv:1907.04268)
Discussion in the context of M-theory on G2-manifolds:
-
Beatriz de Carlos, Andre Lukas, Stephen Morris, Non-perturbative vacua for M-theory on G2 manifolds, JHEP 0412:018 (2004) [arxiv:hep-th/0409255]
which concludes that with taking non-perturbative effects from membrane instantons into account one gets 4d vacua with vanishing and negative cosmological constant (Minkowski spacetime and anti-de Sitter spacetime) but not with positive cosmological constant (de Sitter spacetime). They close by speculating that M5-brane instantons might yield de Sitter spacetime.
-
Johan Blåbäck, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Constructing stable de Sitter in M-theory from higher curvature corrections (arXiv:1902.04053)
which suggests that including higher curvature corrections makes it work
-
Iosif Bena, Alex Buchel, Severin Lüst?, Throat destabilization (for profit and for fun) (arxiv:1910.08094)
Swampland cobordism conjecture
The swampland cobordism conjecture is the hypothesis that consistency of vacua in string theory/M-theory/F-theory (hence their being in the “landscape” instead of the “swampland”) requires (undefined) stringy/quantum gravity-analogs of cobordism groups to vanish:
-
Jacob McNamara, Cumrun Vafa, Cobordism Classes and the Swampland [arXiv:1909.10355, spire:1755441]
-
Miguel Montero, Cumrun Vafa, Cobordism Conjecture, Anomalies, and the String Lamppost Principle, J. High Energ. Phys. 2021, 63 (2021) [arXiv:2008.11729]
-
Markus Dierigl, Jonathan Heckman, On the Swampland Cobordism Conjecture and Non-Abelian Duality Groups, Physical Review D 2021 [arXiv:2012.00013]
-
Hirosi Ooguri, Tadashi Takayanagi, Cobordism Conjecture in AdS (arXiv:2006.13953)
-
David Andriot, Nils Carqueville, Niccolò Cribiori, Looking for structure in the cobordism conjecture, SciPost Phys. 13 (2022) 071 [arXiv:2204.00021, doi:10.21468/SciPostPhys.13.3.071]
-
Ralph Blumenhagen, Christian Kneissl, Chuying Wang, Dynamical Cobordism Conjecture: Solutions for End-of-the-World Branes, J. High Energ. Phys.2023 (2023) 123 [arXiv:2303.03423, doi:10.1007/JHEP05(2023)123]
Relation to topological K-theory and D-brane charge quantization in K-theory:
-
Ralph Blumenhagen, Niccolò Cribiori, Open-Closed Correspondence of K-theory and Cobordism, J. High Energ. Phys. 2022 37 (2022) [arXiv:2112.07678, doi:10.1007/JHEP08(2022)037]
-
Ralph Blumenhagen, Niccolò Cribiori, Christian Kneissl, Andriana Makridou, Dimensional Reduction of Cobordism and K-theory, Journal of High Energy Physics 2023, 181, [doi:10.1007/JHEP03(2023)181, arXiv:2208.01656]
Review:
- Ralph Blumenhagen, Nullifying Cobordism in Quantum Gravity, talk at QFT and Cobordism, CQTS (Mar 2023) web, slides: pdf, video: YT]
A more concrete consequence of this conjecture is claimed (McNamara & Vafa 2019, Sec. 5.2, 2nd paragr.) to be the statement that – paraphrasing/extrapolating somewhat (in line with Blumenhagen & Cribiori 2022; Blumenhagen et al. 2023; Blumenhagen 2023, p. 23): Certain topological brane charges are quantized in Cobordism cohomology; so that, in particular tadpole cancellation of brane charges is to happen in Cobordism cohomology. This kind of statement is also discussed, as a consequence of Hypothesis H, in (see p. 83):
- Hisham Sati, Urs Schreiber, M/F-Theory as Mf-Theory, Rev. Math. Phys. 35 10 (2023) [arXiv:2103.01877, doi:10.1142/S0129055X23500289]
Last revised on March 29, 2024 at 21:34:10. See the history of this page for a list of all contributions to it.