nLab standard model of cosmology
Context
Cosmology
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
Idea
The standard model (in theoretical physics) for the observable universe on the largest length scales of cosmology:
it is an inflationary FRW spacetime with cosmological constant (“dark energy”) and cold dark matter. The technical term for this is the CDM concordance model (where “” is the standard symbol for the cosmological constant and “CDM” is for “cold dark matter”).
The current model assumes that the energy density of the observable universe consists of
-
26.8% dark matter
-
68.3% dark energy.
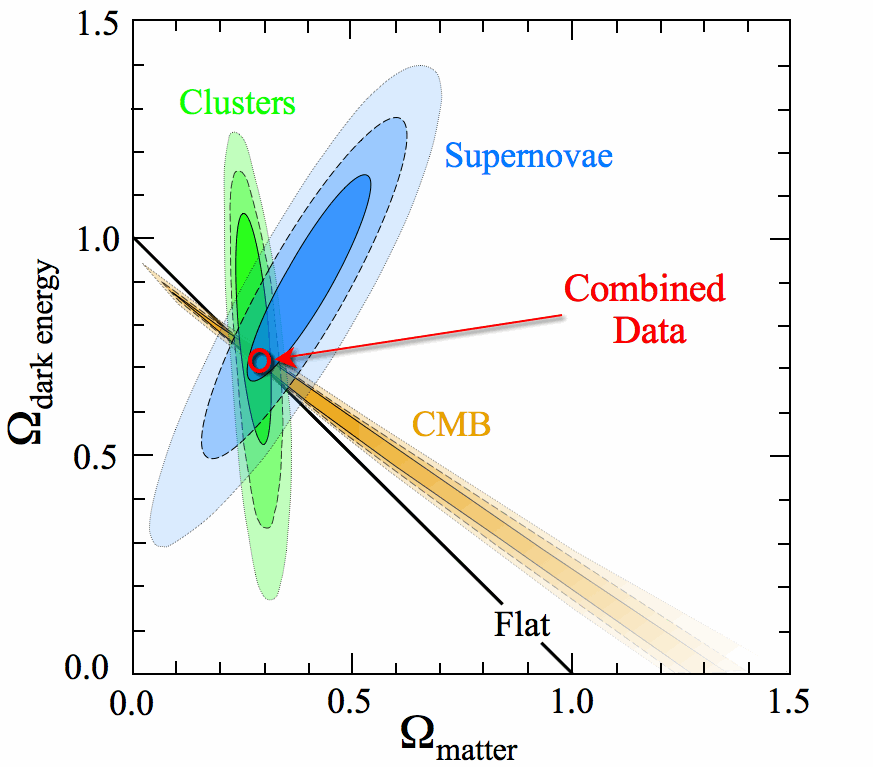
(e.g. Einasto 09, fig 17, here)
Properties
Structure formation
Computer simulation of cosmic structure formation on scales larger than that of galaxies had always shown very good agreement of the standard model of cosmology and observation.
There used to be various discrepancies of cold dark matter-models on the scale of galaxies
But recent analysis seems to show that more fine-grained analysis shows that cold dark matter-models match all of these observations well. See behind the above links for more.
Vacuum energy and Cosmological constant
The renormalization freedom in perturbative quantization of gravity (perturbative quantum gravity) induces freedom in the choice of vacuum expectation value of the stress-energy tensor and hence in the cosmological constant.
For review see Hack 15, section 3.2.1
For more see at cosmological constant here.
Related concepts
standard model of particle physics and cosmology
| theory: | Einstein- | Yang-Mills- | Dirac- | Higgs |
|---|---|---|---|---|
| gravity | electroweak and strong nuclear force | fermionic matter | scalar field | |
| field content: | vielbein field | principal connection | spinor | scalar field |
| Lagrangian: | scalar curvature density | field strength squared | Dirac operator component density | field strength squared + potential density |
References
General
See also the references at cosmology (here).
Lecture notes:
- Matthias Blau, chapter 38 of: Lecture notes on general relativity (web)
Review:
-
Jorge L. Cervantes-Cota, George Smoot, Cosmology today – A brief review, AIP Conf. Proc. 1396 (2011) 28-52 [arXiv:1107.1789, doi:10.1063/1.3647524]
-
Viatcheslav Mukhanov, Quantum Universe, Phys.Usp. 59 (2016) no.10, 1021-1027 (spire:1507528, doi:10.3367/UFNe.2016.07.037857, video recording)
In March 2013, following an accurate processing of available measurement data, the Planck Scientific Collaboration published the highest-resolution photograph ever of the early Universe when it was only a few hundred thousand years old. The photograph showed galactic seeds in sufficient detail to test some nontrivial theoretical predictions made more than thirty years ago. Most amazing was that all predictions were confirmed to be remarkably accurate. With no exaggeration, we may consider it established experimentally that quantum physics, which is normally assumed to be relevant on the atomic and subatomic scale, also works on the scale of the entire Universe, determining its structure with all its galaxies, stars, and planets.
- George Efstathiou, Steven Gratton, The evidence for a spatially flat Universe (arXiv:2002.06892)
Discussion of open problems (see also at inhomogeneous cosmology):
-
Benoit Famaey, Stacy McGaugh, Challenges for Lambda-CDM and MOND (arXiv:1301.0623)
-
Thomas Buchert, Alan A. Coley, Hagen Kleinert, Boudewijn F. Roukema, David L. Wiltshire, Observational Challenges for the Standard FLRW Model, Int. J. Mod. Phys. D 25, 1630007 (2016) (arXiv:1512.03313)
See also:
-
Wikipedia, Lambda-CDM model
-
Jaan Einasto, Dark matter (arXiv:0901.0632) 2009
Possible tension with observation
Possible tensions in the model, regarding determination of the Hubble constant in the early and late universe, apparently observed by various groups, since the late 2010s:
review:
-
L. Verde, T. Treu, Adam G. Riess, Tensions between the Early and the Late Universe, Nature Astronomy (2019) [arXiv:1907.10625, doi:10.1038/s41550-019-0902-0]
-
Snowmass White Paper: Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies, J. High En. Astrophys. 34 (2022) 49-211 [arXiv:2203.06142, doi:10.1016/j.jheap.2022.04.002]
Indication that the tension is not in the data but in systematic errors:
- Freedman et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch (arxiv:1907.05922)
Indication from new data from the James Webb Space Telescope that the old data does not have systematic errors and the tension is in the data:
- Wenlong Yuan?, Adam G. Riess, Stefano Casertano?, Lucas M. Macri?, A First Look at Cepheids in a SN Ia Host with JWST (arXiv:2209.09101)
Review of further observed deviations (such as large-scale inhomogeneties like the KBC void):
- Phillip James E. Peebles, Anomalies in Physical Cosmology [arXiv:2208.05018]
There are possible tensions with high redshift galaxies detected at the James Webb Space Telescope:
- Michael Boylan-Kolchin, Stress Testing ΛCDM with High-redshift Galaxy Candidates, (arXiv:2208.01611)
For testing the standard model of cosmology in light of the James Webb Space Telescope, see
- Nikita Lovyagin, Alexander Raikov, Vladimir Yershov, Yuri Lovyagin, Cosmological Model Tests with JWST. (arXiv:2212.06575)
On the possibility that these tensions could, in part, by a sign/cause of inhomogeneous cosmology violating the widely assumed “cosmological principle”:
- Pavan Kumar Aluri, et al., Is the Observable Universe Consistent with the Cosmological Principle?, Classical and Quantum Gravity 40 9 (2023) [doi:10.1088/1361-6382/acbefc, arXiv:2207.05765]
In AQFT on Curved spacetimes
Discussion in the rigorous context ofAQFT on curved spacetimes includes
-
Klaus Fredenhagen, Thomas-Paul Hack, Quantum field theory on curved spacetime and the standard cosmological model (arXiv:1308.6773)
-
Thomas-Paul Hack, The Lambda CDM-model in quantum field theory on curved spacetime and Dark Radiation (arXiv:1306.3074)
For review see
- Thomas-Paul Hack, section 3.2.1 Cosmological Applications of Algebraic Quantum Field Theory in Curved Spacetimes, Springer 2016 (arXiv:1506.01869, doi:10.1007/978-3-319-21894-6)
Last revised on June 27, 2023 at 05:53:47. See the history of this page for a list of all contributions to it.