nLab anti de Sitter spacetime
Context
Riemannian geometry
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
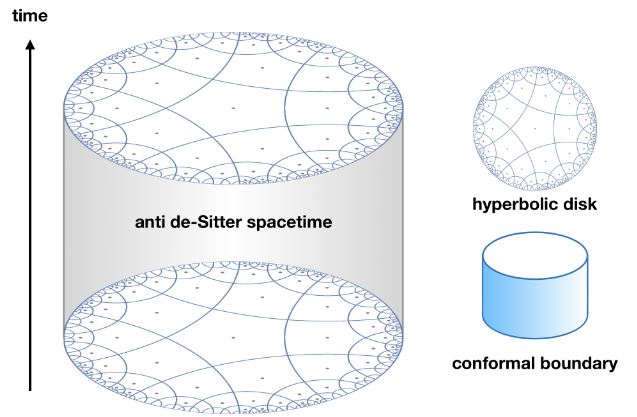
Definition
Up to isometry, the anti de Sitter spacetime of dimension , , is the pseudo-Riemannian manifold whose underlying manifold is the submanifold of the Minkowski spacetime that solves the equation
for some (the “radius” of the spacetime) and equipped with the metric induced from the ambient metric, where denote the canonical coordinates. is homeomorphic to , and its isometry group is .
More generally, one may define the anti de Sitter space of signature as isometrically embedded in the space with coordinates as the sphere .
graphics grabbed from Yan 19
Properties
Coordinate charts
(…)
in horospheric coordinates the AdS metric tensor is
In terms of
this becomes
and with
for
we get
Conformal boundary
(…)
Holography
Asymptotically anti-de Sitter spaces play a central role in the realization of the holographic principle by AdS/CFT correspondence.
In -adic geometry
A 2-adic arithmetic geometry-version of AdS spacetime is identified with the Bruhat-Tits tree for the projective general linear group :
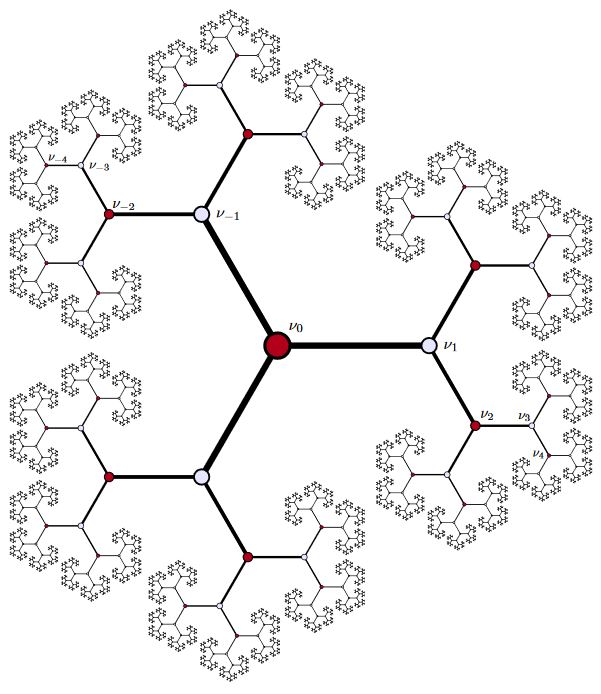
graphics from Casselman 14
In the p-adic AdS/CFT correspondence this may be regarded (at some finite depth truncation) as a tensor network state:
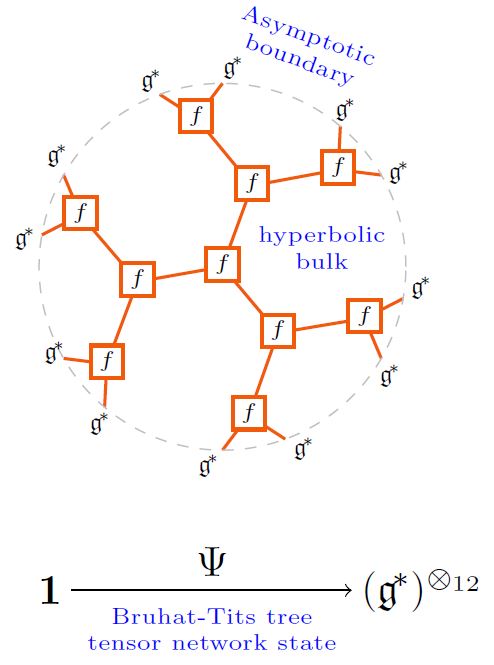
graphics from Sati-Schreiber 19c
and as such validates the Ryu-Takayanagi formula for holographic entanglement entropy.
Related concepts
References
General
Reviews:
-
Leonardo Castellani, Riccardo D'Auria, Pietro Fré, volume 1, chapter I.3.8 of: Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991)
-
Ingemar Bengtsson, Anti-de Sitter space, lecture notes 1998 (pdf)
-
Matthias Blau, chapter 38 of: Lecture notes on general relativity (web)
-
Gary Gibbons, Anti-de-Sitter spacetime and its uses (arXiv:1110.1206)
-
Makoto Natsuume, section 6 of: AdS/CFT Duality User Guide, Lecture Notes in Physics 903, Springer 2015 (arXiv:1409.3575)
-
Leszek M. Sokolowski, The bizarre anti-de Sitter spacetime, International Journal of Geometric Methods in Modern Physics 13 no.9 (2016) 1630016 (arXiv:1611.01118)
See also:
- Wikipedia, anti de Sitter space
Further discussion:
-
Abdelghani Zeghib, On closed anti de Sitter spacetimes, Math. Ann. 310, 695–716 (1998) (pdf)
-
C. Frances, The conformal boundary of anti-de Sitter space-times, in AdS/CFT correspondence: Einstein metrics and their conformal boundaries , 205–216, IRMA Lect. Math. Theor. Phys., 8, Eur. Math. Soc., Zürich, 2005 (pdf)
-
Jiri Podolsky, Ondrej Hruska, Yet another family of diagonal metrics for de Sitter and anti-de Sitter spacetimes, Phys. Rev. D 95, 124052 (2017) (arXiv:1703.01367)
Discussion of thermal Wick rotation on global anti-de Sitter spacetime (which is already periodic in real time) to Euclidean field theory with periodic imaginary time is in
- B. Allen, A. Folacci, Gary Gibbons, Anti-de Sitter space at finite temperature, Physics Letters B Volume 189, Issue 3, 7 May 1987, Pages 304-310 (doi:10.1016/0370-2693(87)91437-7)
Discussion of black holes in anti de Sitter spacetime:
-
Hawking, Stephen W., and Don N. Page. “Thermodynamics of black holes in anti-de Sitter space.” Communications in Mathematical Physics 87.4 (1983): 577-588.
-
M. Socolovsky, Schwarzschild Black Hole in Anti-De Sitter Space (arXiv:1711.02744)
-
Peng Zhao, Black Holes in Anti-de Sitter Spacetime (pdf)
-
Jakob Gath, The role of black holes in the AdS/CFT correspondence (pdf)
Relation to Teichmüller theory:
- Francesco Bonsante, Andrea Seppi, Anti-de Sitter geometry and Teichmüller theory (arXiv:2004.14414)
Phenomenology
- Anjan A. Sen, Shahnawaz A. Adil, Somasri Sen, Do cosmological observations allow a negative ? (arXiv:2112.10641)
As string vacua
On (in-)stability of non-supersymmetric AdS vacua in string theory:
- Iosif Bena, Krzysztof Pilch, Nicholas Warner, Brane-Jet Instabilities, J. High Energ. Phys. 2020, 91 (2020) (arXiv:2003.02851)
pp-Waves as Penrose limits of spacetimes
Discussion of pp-wave spacetimes as Penrose limits (Inönü-Wigner contractions) of AdSp x S^q spacetimes and of the corresponding limit of AdS-CFT duality:
-
David Berenstein, Juan Maldacena, Horatiu Nastase, Section 2 of: Strings in flat space and pp waves from Super Yang Mills, JHEP 0204 (2002) 013 (arXiv:hep-th/0202021)
-
N. Itzhaki, Igor Klebanov, Sunil Mukhi, PP Wave Limit and Enhanced Supersymmetry in Gauge Theories, JHEP 0203 (2002) 048 (arXiv:hep-th/0202153)
-
Nakwoo Kim, Ari Pankiewicz, Soo-Jong Rey, Stefan Theisen, Superstring on PP-Wave Orbifold from Large-N Quiver Gauge Theory, Eur. Phys. J. C25:327-332, 2002 (arXiv:hep-th/0203080)
-
E. Floratos, Alex Kehagias, Penrose Limits of Orbifolds and Orientifolds, JHEP 0207 (2002) 031 (arXiv:hep-th/0203134)
-
E. M. Sahraoui, E. H. Saidi, Metric Building of pp Wave Orbifold Geometries, Phys.Lett. B558 (2003) 221-228 (arXiv:hep-th/0210168)
Review:
-
Darius Sadri, Mohammad Sheikh-Jabbari, The Plane-Wave/Super Yang-Mills Duality, Rev. Mod. Phys. 76:853, 2004 (arXiv:hep-th/0310119)
-
Badis Ydri, Section 3.1.10 of: Review of M(atrix)-Theory, Type IIB Matrix Model and Matrix String Theory (arXiv:1708.00734), published as: Matrix Models of String Theory, IOP 2018 (ISBN:978-0-7503-1726-9)
See also:
- Michael Gutperle, Nicholas Klein, A Penrose limit for type IIB solutions (arXiv:2105.10824)
Last revised on December 22, 2021 at 16:48:29. See the history of this page for a list of all contributions to it.