Schreiber Differential Cohomotopy implies intersecting brane observables
an article that we have written:
Differential Cohomotopy implies
intersecting brane observables
via configuration spaces and chord diagrams
Advances in Theoretical and Mathematical Physics
26 4 (2022) 957-1051
doi:10.4310/ATMP.2022.v26.n4.a4
download file:
-
v2: pdf
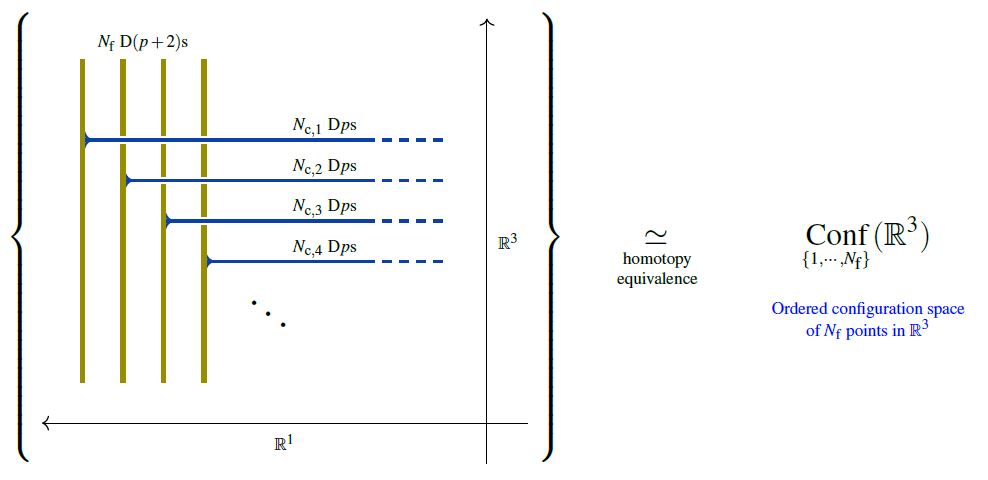
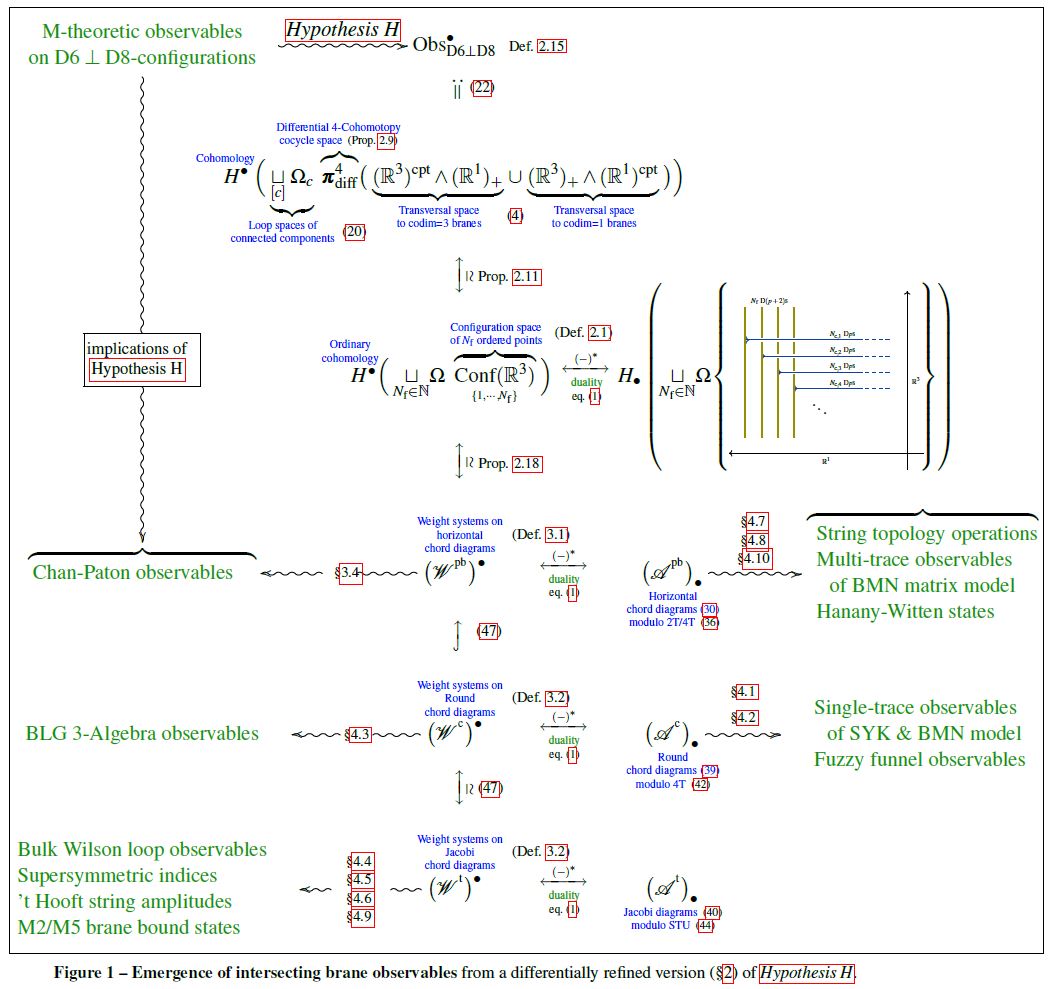
Abstract: We introduce a differential refinement of Cohomotopy cohomology theory, defined on Penrose diagram spacetimes, whose cocycle spaces are unordered configuration spaces of points. First we prove that brane charge quantization in this differential 4-Cohomotopy theory implies intersecting p/(p+2)-brane moduli given by ordered configurations of points in the transversal 3-space. Then we show that the higher observables on these brane moduli, conceived as the cohomology of the Cohomotopy cocycle space, are given by weight systems on horizontal chord diagrams and reflect a multitude of effects expected in the quantum theory of Dp-D(p+2) brane intersections: condensation to stacks of coincident branes and their Chan-Paton factors, fuzzy funnel states and BLG 3-algebra observables, AdS3-gravity observables supersymmetric indices of Coulomb branches, M2/M5-brane bound states in the BMN matrix model and the Hanany-Witten rules, as well as gauge/gravity duality between all these. We discuss this in the context of the Hypothesis H that the M-theory C-field is charge-quantized in Cohomotopy cohomology theory.
Talk notes:
-
Some Quantum States of M-Branes under Hypothesis H
talk at Centre for Research in String Theory
Queen Mary University London, 2021
-
Microscopic brane physics from Cohomotopy theory
talk at M-Theory and Mathematics
NYU Abu Dhabi, 2020
-
Equivariant Cohomotopy of toroidal orbifolds
talk at Prof. Sadok Kallel‘s group seminar
AUS Sharjah, 2019
Followup:
Related articles (Hypothesis H)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Twisted Cohomotopy implies M-theory anomaly cancellation on 8-manifolds
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
-
Equivariant Cohomotopy implies orientifold tadpole cancellation
-
Lift of fractional D-brane charge to equivariant Cohomotopy theory
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Twisted Cohomotopy implies twisted String structure on M5-branes
Last revised on March 21, 2023 at 13:42:40. See the history of this page for a list of all contributions to it.