Schreiber Hypothesis H

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Authors |
Contents

Contents

Idea

Hypothesis H is a hypothesis about the mathematical formulation of the theory of fundamental physics known as M-theory. The core statement of the hypothesis is that quantum charge quantization in M-theory happens in the non-abelian cohomology theory called Cohomotopy (in more detail: twisted Cohomotopy). This originates with an observation due to Sati 2013 (Sec. 2.5) and has become the theme of a research program developed by Hisham Sati and Urs Schreiber, see the list of references below.

(In a play on how the “M” in “M-theory” has been said to be either for “Membrane” or for “Mystery”, so the “H” in “Hypothesis H” may be read as being either for “Homotopy” or for “Hisham”.)


The open problem of formulating M-Theory

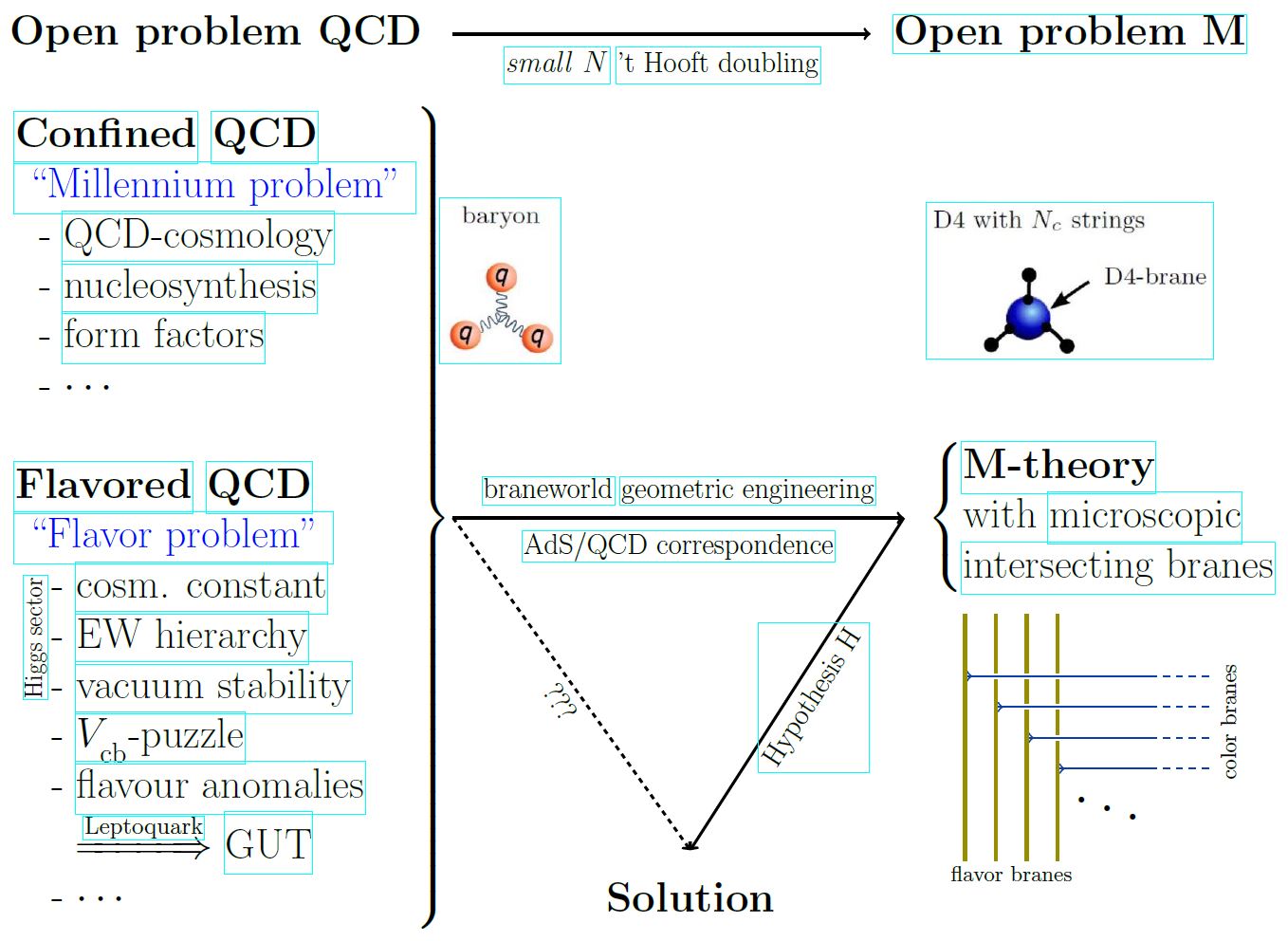
It is an open problem to mathematically formulate M-theory: Supposedly a single coherent theory of physics whose various limiting cases reproduce the zoo of perturbative string theories (HET/I/IIA/IIB&F/11d SuGra) and the expected dualities relating them; but which also makes mathematical sense of non-perturbative D-/M-brane physics, and hence solves, via intersecting D-brane models of confined quantum Yang-Mills theory (holographic QCD), the last of the Millennium Problems:

In the physics-minded string theory community, parts of the literature tends to forget or downplay the conjectural nature of many assumptions and leaps of faiths that are being made when it comes to discussion of D-brane/M-brane dynamics and generally of non-perturbative effects in string theory. More widely recognized is the fact that the theory of coincident M5-branes is missing, together with the formulation of its expected decoupling limit to the D=6 N=(2,0) SCFT – but of course these major open problems are but one aspect of full M-theory. For string-theoretic references that do highlight the open problem of formulating M-theory see at M-theory – The open problem.

In mathematics, it is rare but not unfamiliar that an open problem is not the proof of a theorem within an established theory, but is the establishing of a theory in the first place. A famous example of such a situation is the search for a theory of “absolute geometry” over the “field with one element”. In this analogy, the various perturbative string theories (HET, I, IIA, IIB and their KK-compactified perturbative string theory vacua) correspond to arithmetic geometries over base prime fields 𝔽 p\mathbb{F}_p for p≥2p \geq 2, and the would-be M-theory corresponds to a theory of a “field with one element” that unifies and completes all this, by describing it at a deeper level (literally: a deeper base).

Hence the task here is to conjure a mathematical theory 𝒳\mathcal{X}, hypothesize that and explain how 𝒳\mathcal{X} is the putative M-theory, and then rigorously work out the mathematical implications of 𝒳\mathcal{X} in order to check to which extent they include the required design criterion “𝒳⇒ST\mathcal{X} \Rightarrow ST”. To the extent that 𝒳\mathcal{X} implies known or expected phenomena in perturbative string theory the hypothesis that 𝒳\mathcal{X} is M-theory finds support, to the extent that it doesn’t 𝒳\mathcal{X} needs to be modified to or be replaced by some 𝒳′\mathcal{X}', and the process re-started.


Hypothesis H

Statement

In the large-scale/low-energy limit of M-theory given by D=11 supergravity, the covariant phase space must consist of super-torsion free super orbi ℝ 10,1|32\mathbb{R}^{10,1\vert \mathbf{32}}-folds equipped with a suitable higher gauge field: the C-field.

The first ingredient of a non-perturbative quantization of this phase space must be a choice of Dirac charge quantization-condition for the C-field.

Hypothesis H: (FSS 19b,FSS 19c) The C-field is charge quantized in J-twisted Cohomotopy cohomology theory.


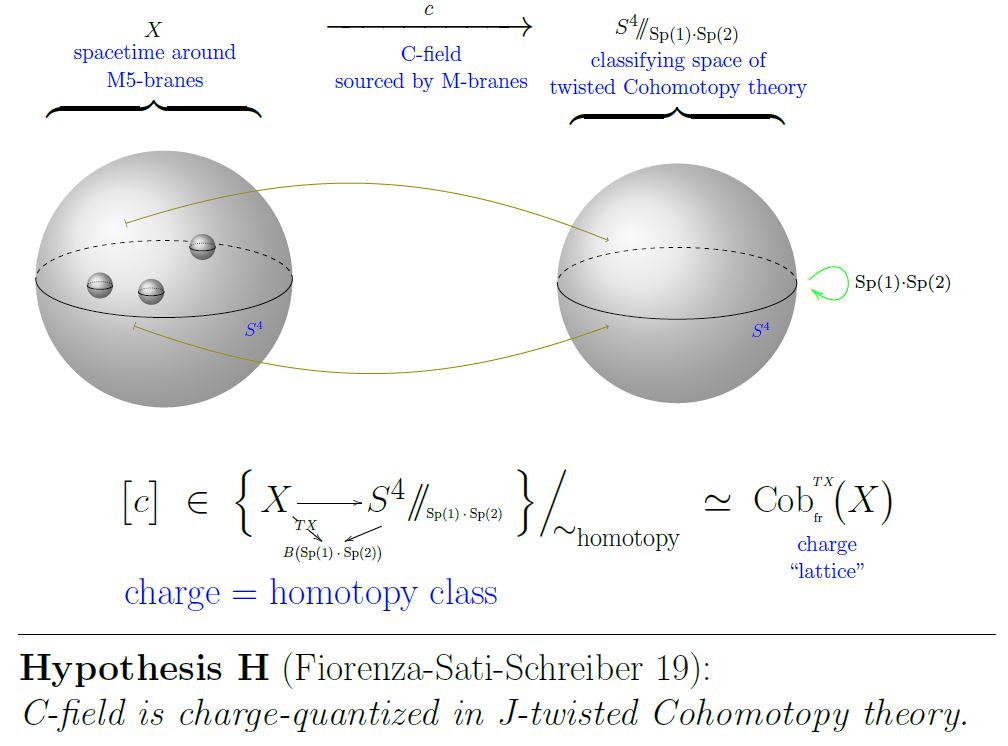
Motivation from homotopy theoretic re-analysis of the brane-scan

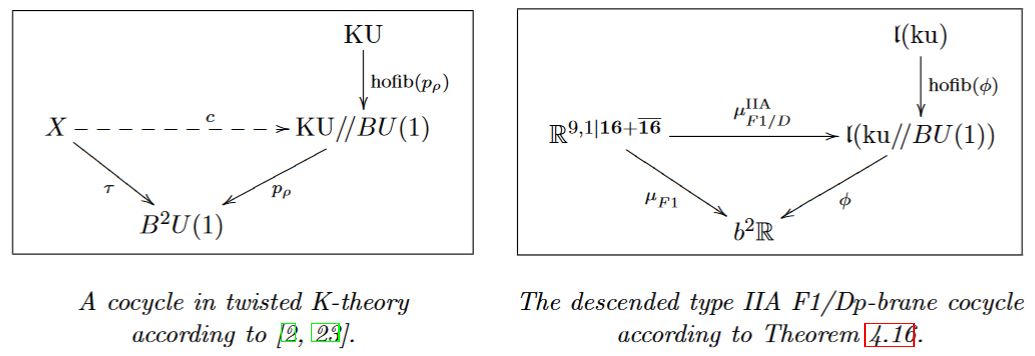
The Hypothesis H (above) is motivated from re-analysis (based on Sati 13, Sec. 2.5 see FSS 19a for comprehensive review) of super p-brane WZ terms in super homotopy theory. The resulting brane bouquet proves that – in the approximation of rational homotopy theory – M-brane charge is in rational Cohomotopy in exactly the same way that D-brane charge is in twisted K-theory.

Detailed lecture note on this point are at geometry of physics – fundamental super p-branes, in the section M-Flux fields.


Implications

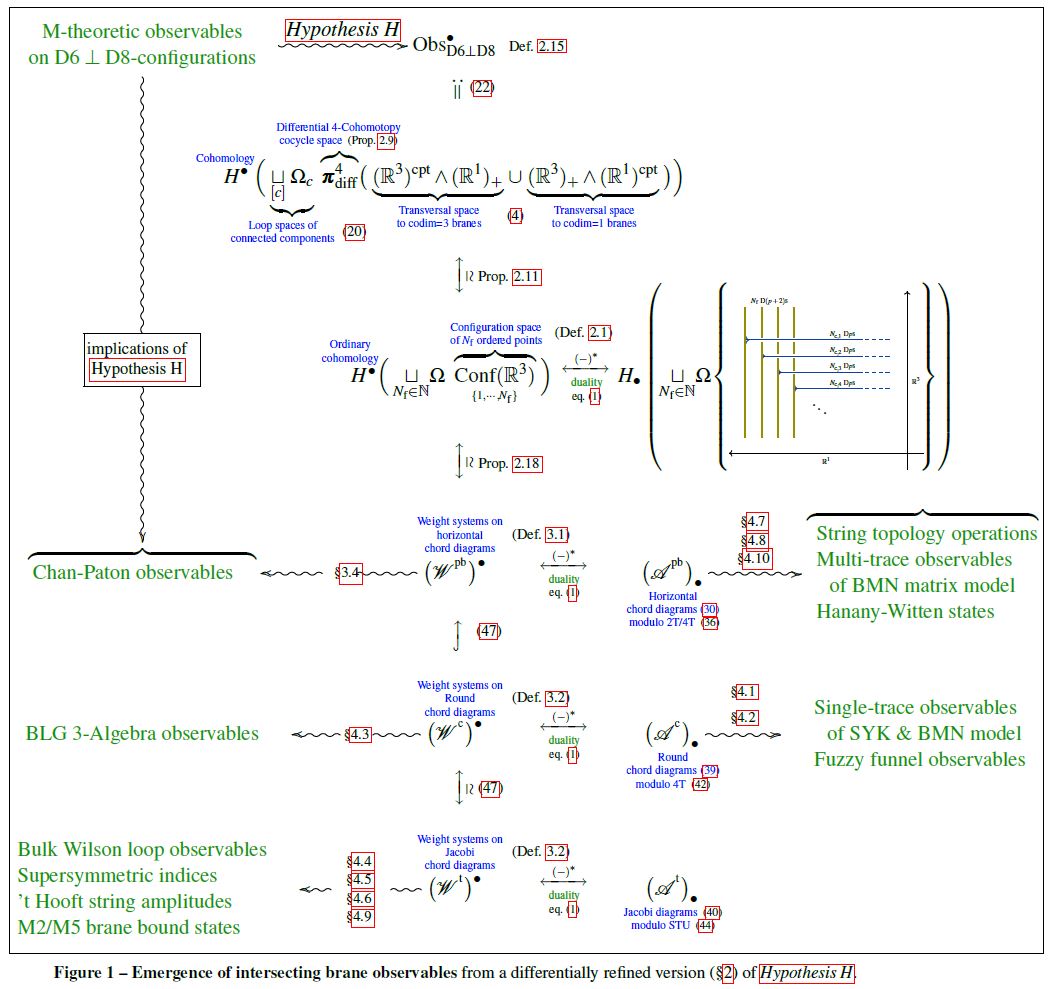
Assuming Hypothesis H, we have a well-defined covariant phase space and may rigorously derive properties of the resulting states and observables. These are the implications of Hypothesis H. To the extent that these implications match known facts of perturbative string theory and to the extent that they match folklore about M-theory, Hypothesis H finds support, to the extend that they do not Hypothesis H may need to be adjusted or abandoned.

Anomaly cancellation

What physicists call anomalies are what mathematician call obstructions to the construction of a physical theory. Hence cancellation of all anomalies in every quantum field theory that folklore expects to be a limiting case of M-theory is strictly necessary for M-theory to exist: Any remaining anomaly is an obstruction against the existence of the theory that it is an anomaly of.

A long list of anomaly cancellation conditions in M-theory has been argued for in the literature, obtained from a variety of different arguments and under various assumptions, but supported by a web of consistency checks.


Theorem (FSS 19b, FSS 19c, SS 19a)

Hypothesis H implies the following list of anomaly cancellation consistency conditions expected in the M-theory folklore:

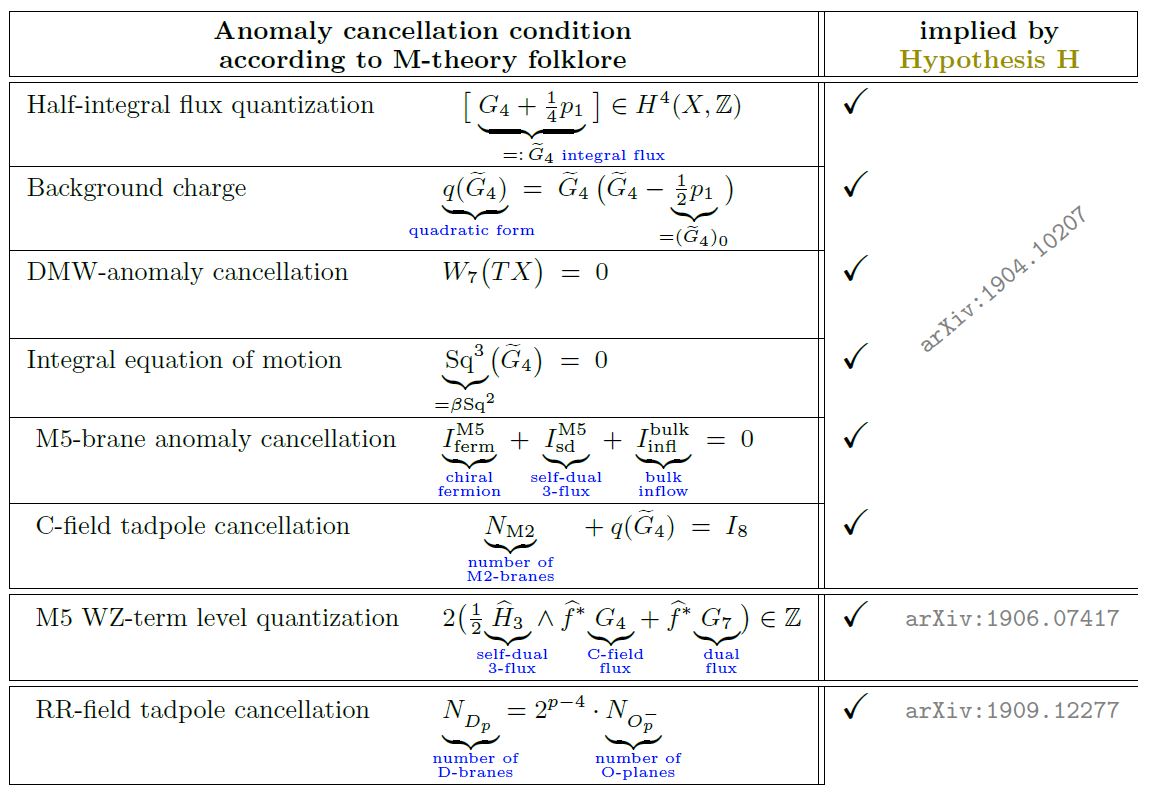
On curved but non-singular 8-manifolds

Here is a quick survey of the implications of Hypothesis H on expected M-theory anomaly cancellation conditions for M-theory on 8-manifolds:

download: pdf

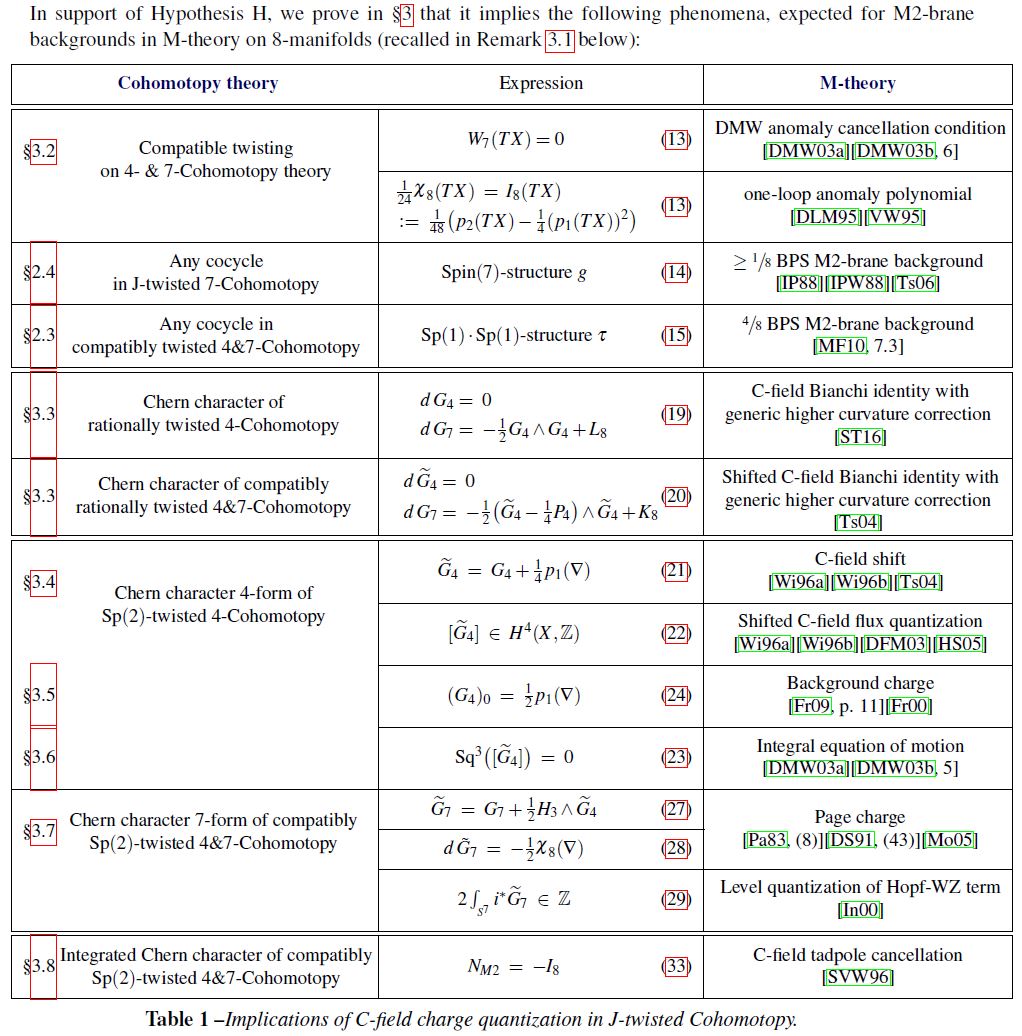
On flat but singular orbifolds:


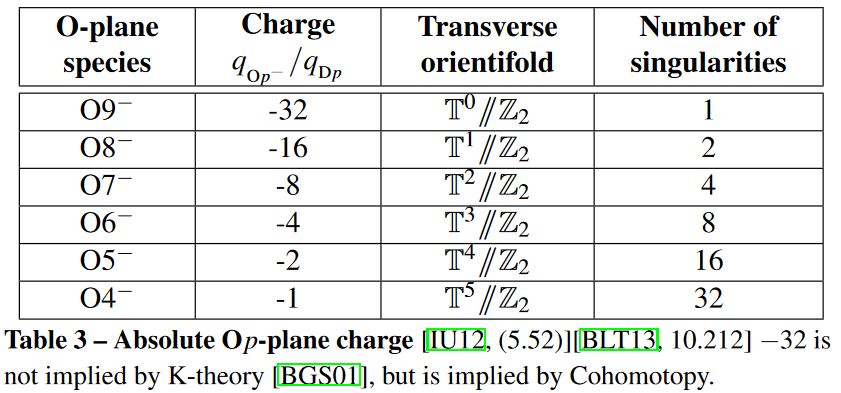
Hypothesis H implies RR-field tadpole cancellation on flat orbifolds with ADE-singularities, including the absolute O-plane charge and hence the SemiSpin(32)-gauge group of type I' string theory, dually of heterotic string theory. This is the heart of what came to be known as the “first string theory revolution” (Schwarz 07).

From SS 19a:

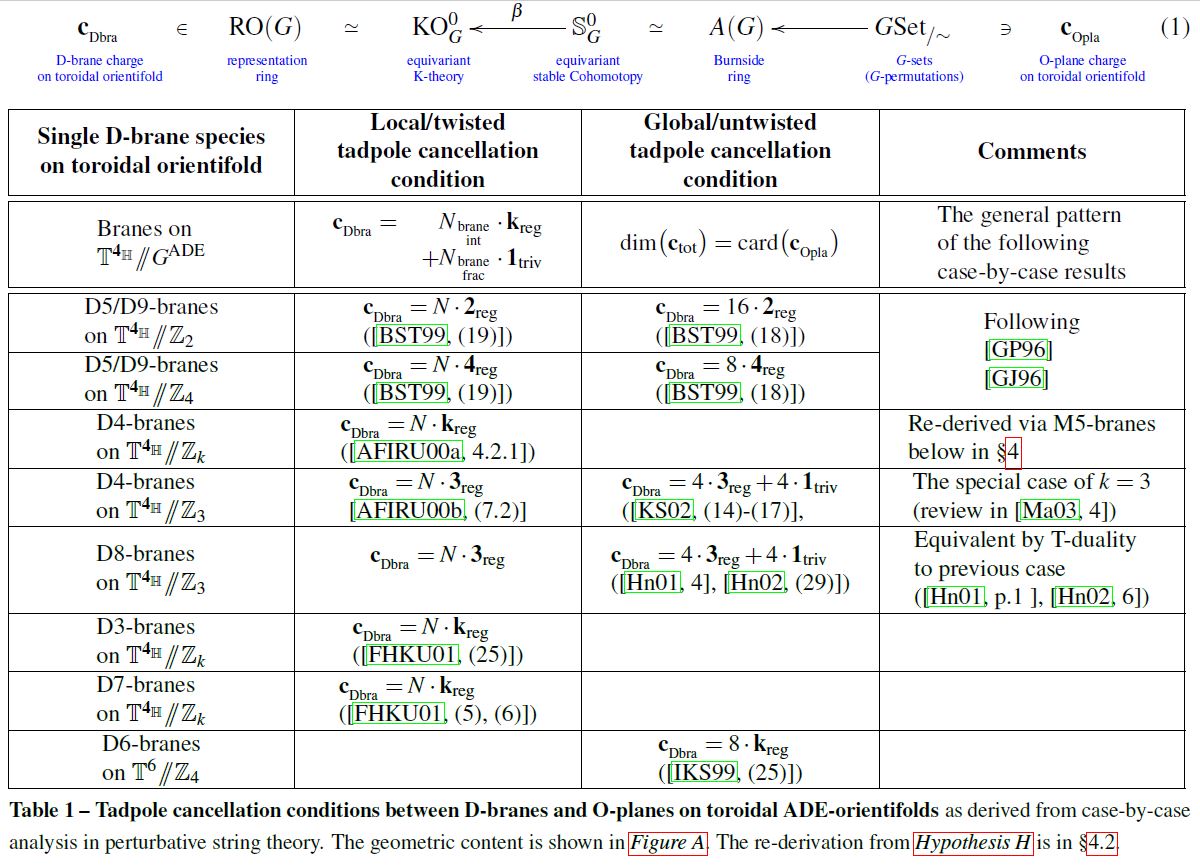
Microscopic brane physics

The core aspect of D-brane physics is the folklore (see BMSS 19, p. 3) that, at low energy, coincident D-branes carry Yang-Mills gauge theory on their worldvolumes. This is the starting point of geometric engineering of quantum field theory in intersecting D-brane models and without this phenomenon, string theory would be irrelevant for phenomenology.

Moreover, folklore has it (but see the issues with the nonabelian DBI action here) that at small-scale/high-energy intersecting branes show the deep quantum phenomena associated with monopoles in Yang-Mills theory, which ultimately lead to the partial formulation of M-theory via the BFSS matrix model and the BMN matrix model.

Hypothesis H implies that the states and observables of M-theory reflect the following expected phenomena for Dp-D(p+2)-brane intersections:

From SS 19c:


FAQ


References for the FAQ:

  • E. Diaconescu, G. Moore, E. Witten, E 8E_8 Gauge Theory, and a Derivation of K-Theory from M-Theory, Adv. Theor. Math. Phys. 6:1031-1134, 2003 (arXiv:hep-th/0005090), summarised in: A Derivation of K-Theory from M-Theory (arXiv:hep-th/0005091)

  • M Hopkins, I. Singer, Quadratic Functions in Geometry, Topology, and M-Theory, J. Differential Geom. Volume 70, Number 3 (2005), 329-452 (arXiv:math.AT/0211216, euclid:1143642908)

  • E. Diaconescu, D. Freed, G. Moore, The MM-theory 3-form and E 8E_8-gauge theory, chapter in: Elliptic Cohomology Geometry, Applications, and Higher Chromatic Analogues, Cambridge University Press 2007 (arXiv:hep-th/0312069, doi:10.1017/CBO9780511721489)

  • V. Mathai, H. Sati, Some Relations between Twisted K-theory and E8 Gauge Theory, JHEP 0403:016, 2004 (arXiv:hep-th/0312033, doi:10.1088/1126-6708/2004/03/016)

  • H. Sati, Framed M-branes, corners, and topological invariants, J. Math. Phys. 59 (2018), 062304 (arXiv:1310.1060)

  • D. Fiorenza, H. Sati, U. Schreiber, The WZW term of the M5-brane and differential cohomotopy, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557, doi:10.1063/1.4932618)

  • D. Fiorenza, H. Sati, U. Schreiber, Rational sphere valued supercocycles in M-theory and type IIA string theory, J. Geom. Phys., Vol 114 (2017) (arXiv:1606.03206, doi:10.1016/j.geomphys.2016.11.024)

  • V. Braunack-Mayer, H. Sati, U. Schreiber, Gauge enhancement of super M-branes via parametrized stable homotopy theory, Comm. Math. Phys. 371: 197 (2019) (arXiv:1806.01115, doi:10.1007/s00220-019-03441-4)

  • S. Burton, H. Sati, U. Schreiber, Lift of fractional D-brane charge to equivariant Cohomotopy theory, J. Geom. Phys., 2020 (in print) (arXiv:1812.09679)

  • D. Fiorenza, H. Sati, U. Schreiber, The rational higher structure of M-theory, in: Proceedings of Higher Structures in M-Theory 2018, Fortsch. Phys. 2019 (arXiv:1903.02834, doi:10.1002/prop.201910017)

  • D. Fiorenza, H. Sati, U. Schreiber, Twisted Cohomotopy implies M-Theory anomaly cancellation on 8-manifolds, Comm. Math. Phys. 377(3), 1961-2025 (2020) (arXiv:1904.10207, doi:10.1007/s00220-020-03707-2)

  • D. Fiorenza, H. Sati, U. Schreiber, Twisted Cohomotopy implies level quantization of the full 6d Wess-Zumino-term of the M5-brane, Comm. Math. Phys. 2020 (in print) (arXiv:1906.07417)

  • D. Fiorenza, H. Sati, U. Schreiber, Twistorial Cohomotopy Implies Green-Schwarz anomaly cancellation (arXiv:2008.08544)

  • H. Sati, U. Schreiber, Equivariant Cohomotopy implies orientifold tadpole cancellation J. Geom. Phys. Vol 156, 2020, 103775 (arXiv:1909.12277, doi:10.1016/j.geomphys.2020.103775)

  • H. Sati, U. Schreiber, Differential Cohomotopy implies intersecting brane observables via configuration spaces and chord diagrams (arXiv:1912.10425)

  • H. Sati, U. Schreiber, Twisted Cohomotopy implies M5-brane anomaly cancellation (arXiv:2002.07737)

  • H. Sati, U. Schreiber, The character map in equivariant twistorial Cohomotopy implies the Green-Schwarz mechanism with heterotic M5-branes (arXiv:2011.06533)

  • H. Sati, M-theory and cohomotopy, talk at M-Theory and Mathematics, NYUAD 2020 (pdf)

  • U. Schreiber, Microscopic brane physics from Cohomotopy theory, talk at M-Theory and Mathematics, NYUAD 2020 (pdf)


References

Motivation by results in rational Cohomotopy

Hypothesis H is motivated by analysis of super p-brane WZ terms in super homotopy theory, which proves that – in the approximation of rational homotopy theory – M-brane charge is in rational Cohomotopy in exactly the same way that D-brane charge is in twisted K-theory.

This is due to:

and was further developed in:

Exposition and review of the rational situation is in:

Partial derivation of the M5-brane-model at this rational level:

On U-duality (and possibly mysterious duality) as automorphisms of iterated (rational) cyclic loop spaces of the (rational) 4-sphere:

Formulation in full Cohomotopy theory

The detailed form of the Hypothesis H (that the above rational situation should lift to full twisted equivariant differential Cohomotopy theory) was formulated, and first consistency checks were made, in:

See also:

Exposition and talk notes

See also:

Last revised on January 15, 2023 at 08:21:24. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (71 revisions) Print Source