Schreiber Fundamental weight systems are quantum states
An article that we have written:
-
David Corfield, Hisham Sati, Urs Schreiber
Fundamental weight systems are quantum states
Letters in Mathematical Physics
113 112 (2023)
doi:10.1007/s11005-023-01725-4
download:
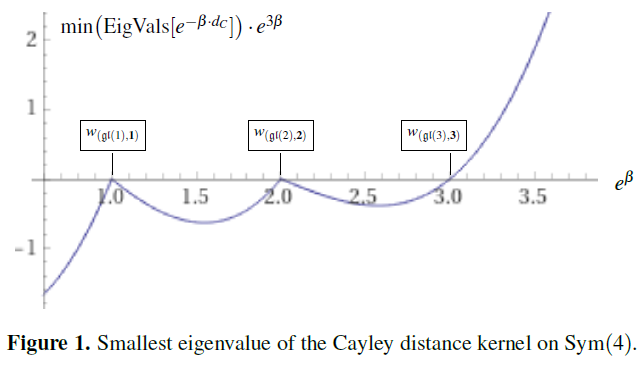
Abstract. Weight systems on chord diagrams play a central role in knot theory and Chern-Simons theory; and more recently in stringy quantum gravity. We highlight that the noncommutative algebra of horizontal chord diagrams is canonically a star-algebra, and ask which weight systems are positive with respect to this structure; hence we ask: Which weight systems are quantum states, if horizontal chord diagrams are quantum observables? We observe that the fundamental -weight systems on horizontal chord diagrams with strands may be identified with the Cayley distance kernel at inverse temperature on the symmetric group on elements. In contrast to related kernels like the Mallows kernel, the positivity of the Cayley distance kernel had remained open. We characterize its phases of indefinite, semi-definite and definite positivity, in dependence of the inverse temperature ; and we prove that the Cayley distance kernel is positive (semi-)definite at for all . In particular, this proves that all fundamental -weight systems are quantum states, and hence so are all their convex linear combinations. We close with briefly recalling how, under our “Hypothesis H”, this result impacts on the identification of bound states of multiple M5-branes.
Followup by:
-
Dror Bar-Natan, AcademicPensieve 2021-05,
The Cayley distance kernel following
arXiv://2105.0287by Corfield, Sati, and Schreiber -
Carlo Collari, A note on weight systems which are quantum states, Can. Math. Bull. (2023) [arXiv:2210.05399, doi:10.4153/S0008439523000206]
Followup to:

Talk notes:
-
Some Quantum States of M-Branes under Hypothesis H
talk at Centre for Research in String Theory
Queen Mary University London, 2021
More background and context:
Last revised on December 9, 2023 at 14:24:04. See the history of this page for a list of all contributions to it.