nLab Lie algebra weight system
Context
Knot theory
Examples/classes:
Types
Related concepts:
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Contents
- Idea
- Properties
- Ubiquity
- Stringy weight systems span classical Lie algebra weight systems
- Relation to Adams operations
- As expectation values of single trace observables
- Chord diagrams as multi-trace observables in the BMN matrix model
- Related concepts
- References
Idea
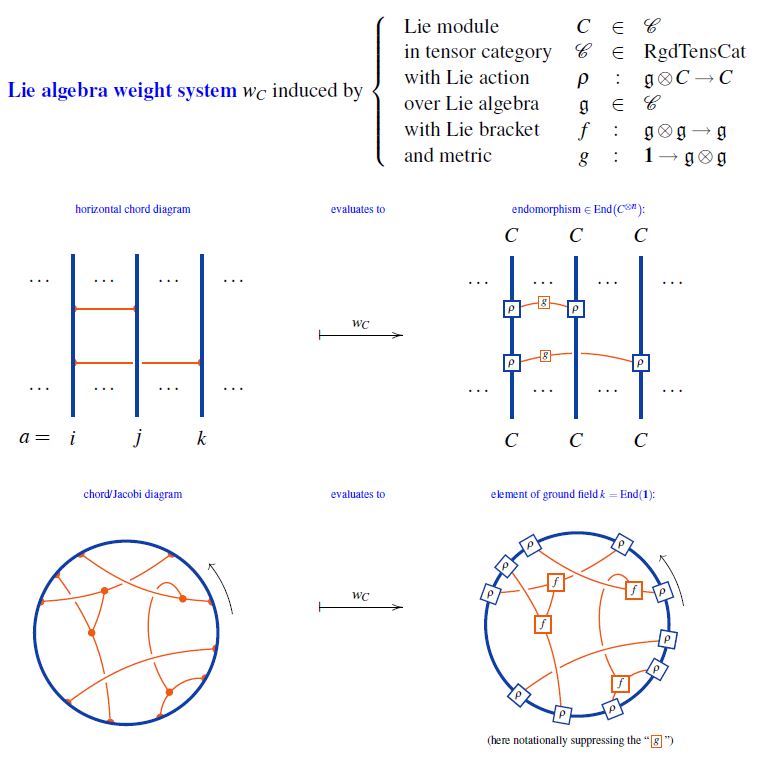
In knot theory, a large class of weight systems arises from reading a (horizontal) chord diagram as a string diagram in the evident way, and then labeling it by the structure morphisms of a metric Lie algebra object equipped with a metric Lie algebra representation internal to a suitable tensor category.
graphics from Sati-Schreiber 19c
This does yield weight systems, because – using that chord diagrams modulo 4T are Jacobi diagrams modulo STU – the required STU-relations translate into the structural equations satisfied by Lie modules (Jacobi identity and Lie action property); see Roberts & Willerton 06, Theorem 3.1, following Vaintrob 94, Vogel 11 following Bar-Natan 95, 2.4, Bar-Natan 96 following Kontsevich 94.
The weight systems arising this way are called Lie algebra weight systems.
Properties
Ubiquity
On round chord diagrams
Examples of weight systems on (ordinary, round) chord diagrams which are not Lie algebra weight systems are rare. Originally it was conjectured that none exist (Bar-Natan 95, Conjecture 1, Bar-Natan & Stoimenow 97, Conjecture 2.4).
Eventually, a (counter-)example of a weight system which at least does not arise from any finite-dimensional super Lie algebra was given in Vogel 11.
On horizontal chord diagrams
For horizontal chord diagrams we have:
-
all horizontal weight systems are partitioned Lie algebra weight systems (Bar-Natan 96)
-
the fundamental -weight system coincides with the Cayley distance kernel at inverse temperature (CSS21)
Stringy weight systems span classical Lie algebra weight systems
stringy weight systems span classical Lie algebra weight systems
Relation to Adams operations
On the vector space of Jacobi diagrams modulo STU-relations (equivalently chord diagrams modulo 4T relations) there is a system of linear maps (for , )
which respect the coalgebra structure and satisfy
and as such are (dually) analogous to the Adams operations on topological K-theory.
(Bar-Natan 95, Def. 3.11 & Theorem 7)
In fact, when evaluated in Lie algebra weight systems and under the identification (see here) of the representation ring of a compact Lie group with the -equivariant K-theory of the point, these Adams operations on Jacobi diagrams correspond to the Adams operations on equivariant K-theory:
For more see at Adams operation on Jacobi diagrams.
As expectation values of single trace observables
We discuss how Lie algebra weight systems on round chord diagrams arise in quantum field theory and statistical mechanics as expectation values of suitable single trace observables subject to Wick's theorem.
So consider
-
be a metric Lie algebra, with metric denoted ,
-
be a finite-dimensional Lie algebra representation of .
For comparison with traditional literature, choose
-
a linear basis of
-
a linear basis of
In terms of these linear bases, the representation is given by a sequence of square matrices such that
with the Einstein summation convention understood here and in the following.
We write for the components of the Lie algebra metric in this basis, and write
With all this understood, a field/random variable with values in is
for scalar field components .
Now assume that the are free fields/random variables with Gaussian distribution, hence such that
and such that Wick's theorem applies to higher moments:
etc.
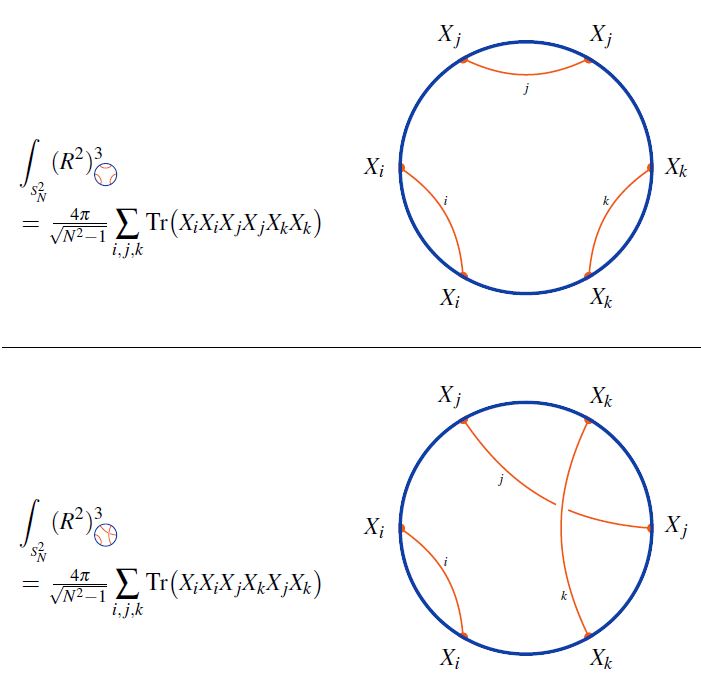
Consider the expectation values of single trace observables:
Using Wick's theorem, they are given by
etc.
Here Wick's theorem in the first lines is given by a sum over linear chord diagrams, and the trace then serves to close these to round chord diagrams:

from Sati-Schreiber 19c
The values of the traces in the last line are the values of the Lie algebra weight system on the chord diagram which reflects the Wick-contractions modulo cyclic permutation.
Essentially this observation (specifically for SYK-model-like systems and without mentioning of weight systems) appears in GGJJV 18, Section 2.2, Jia-Verbaarschot 18, Section 4, BNS 18, Section 2.1, BINT 18, Section 2, Narovlansky 19, Slides 5-21.
Chord diagrams as multi-trace observables in the BMN matrix model
The supersymmetric states of the BMN matrix model are temporally constant complex matrices which are complex metric Lie representations of su(2) (interpreted as fuzzy 2-sphere noncommutative geometries of giant gravitons or equivalently as fuzzy funnels of D0-D2 brane bound states).
A fuzzy 2-sphere-rotation invariant multi-trace observable on these supersymmetric states is hence an expression of the following form:
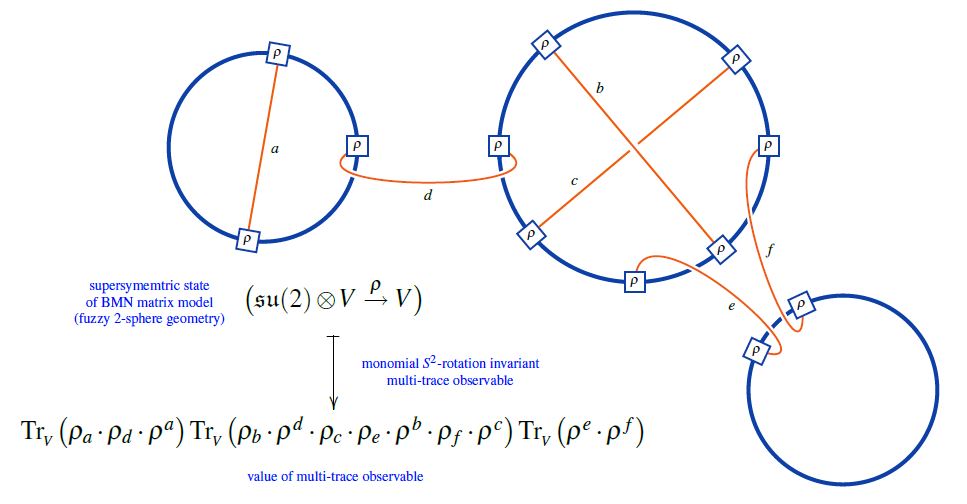
(from Sati-Schreiber 19c)
Here we are showing the corresponding string diagram/Penrose notation for metric Lie representations, which makes manifest that
-
these multi-trace observables are encoded by Sullivan chord diagrams
-
their value on the supersymmetric states is the evaluation of the corresponding Lie algebra weight system on .
Or equivalently, if is a horizontal chord diagram whose -permuted closure is (see here) then the values of the invariant multi-trace observables on the supersymmetric states of the BMN matrix model are the evaluation of on , as shown here:
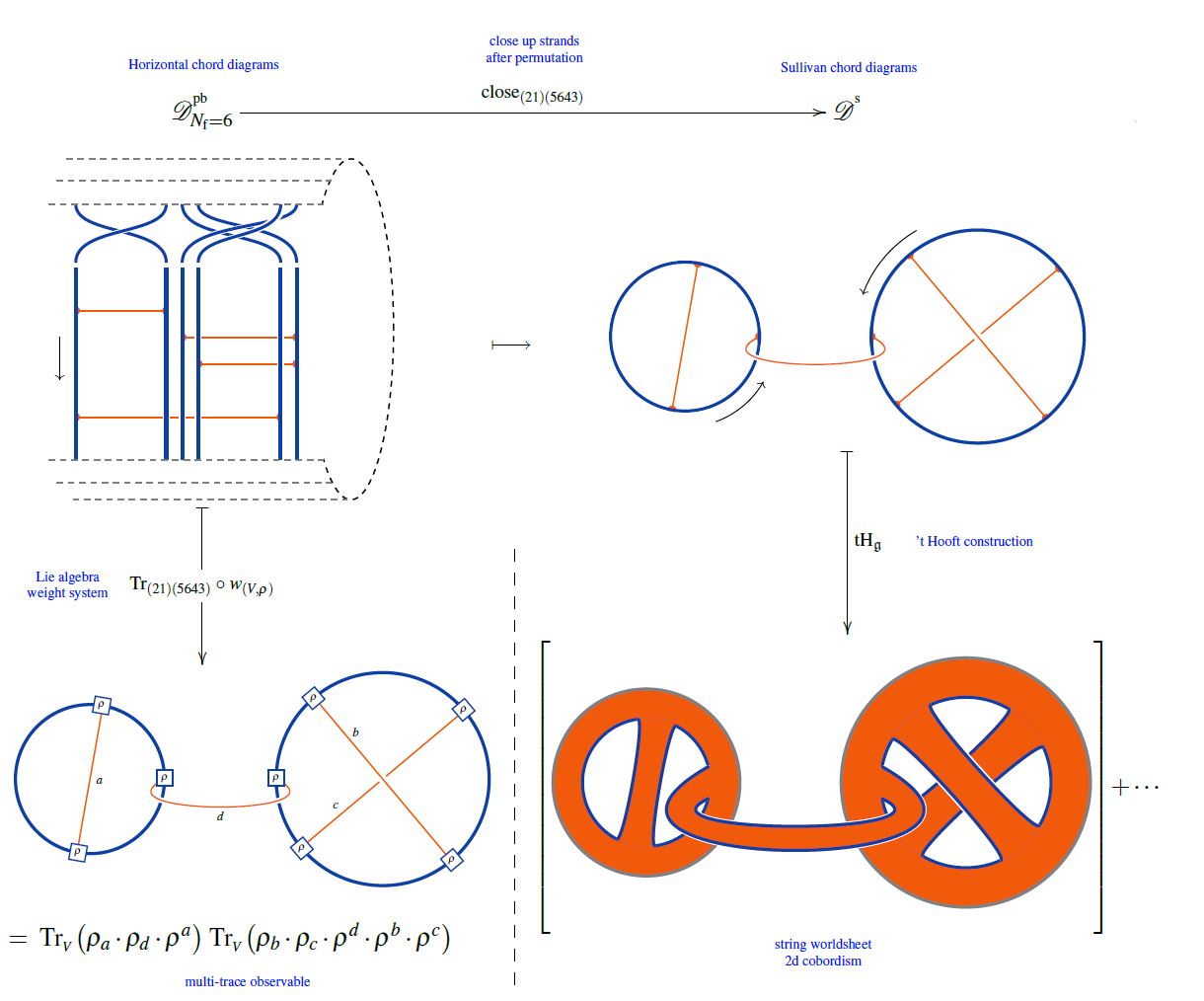
(from Sati-Schreiber 19c)
But since all horizontal weight systems are partitioned Lie algebra weight systems this way, this identifies supersymmetric states of the BMN matrix model as seen by invariant multi-trace observables as horizontal chord diagrams evaluated in Lie algebra weight systems.
Related concepts
| chord diagrams | weight systems |
|---|---|
| linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams | Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems |
References
General
Lie algebra weight systems motivated from Yang-Mills theory Feynman amplitudes:
- Predrag Cvitanović, Group theory for Feynman diagrams in non-Abelian gauge theories, Phys. Rev. D14 (1976) 1536-1553 (doi:10.1103/PhysRevD.14.1536, spire:108133, pdf)
The concept of round Lie algebra weight systems for Chern-Simons theory with Wilson lines originates around
-
Maxim Kontsevich, Feynman diagrams and low-dimensional topology, First European Congress of Mathematics, 1992, Paris, vol. II, Progress in Mathematics 120, Birkhäuser (1994), 97–121 (pdf)
-
Dror Bar-Natan, Section 2.4 of: On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)
and for horizontal weight systems in
- Dror Bar-Natan, Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 (arxiv:q-alg/9607001)
reviewed in
- Dror Bar-Natan, Alexander Stoimenow, Section 2.2 of: The Fundamental Theorem of Vassiliev Invariants, in: Geometry and Physics, Lecture Notes in Pure and Applied Mathematics, volume 184, Marcel Dekker Inc. 1996 (arXiv:q-alg/9702009, ISBN:0-8247-9791-4)
Discussion of fundamental -weight systems in terms of Cayley distance kernels on the symmetric group:
- David Corfield, Hisham Sati, Urs Schreiber: Fundamental weight systems are quantum states (arXiv:2105.02871)
Via string diagrams
From the construction given in Bar-Natan 95, Section 2.4 the interpretation of Lie algebra weight systems in terms of string diagrams for Lie algebra objects in tensor categories is evident, but standard textbooks in knot theory/combinatorics do not pick this up:
-
Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Chapter 6 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)
-
David Jackson, Iain Moffat, Section 14 of: An Introduction to Quantum and Vassiliev Knot Invariants, Springer 2019 (doi:10.1007/978-3-030-05213-3)
The interpretation of Lie algebra weight systems as string diagram-calculus and generalization to Lie algebra objects (motivated by generalization at least to super Lie algebras) is made more explicit in
-
Arkady Vaintrob, Vassiliev knot invariants and Lie S-algebras, Mathematical Research Letters1, 579–595 (1994) (pdf)
-
Pierre Vogel, Algebraic structures on modules of diagrams, Journal of Pure and Applied Algebra, Volume 215, Issue 6, June 2011, Pages 1292-1339 (doi:10.1016/j.jpaa.2010.08.013, pdf)
and fully explicit in
- Justin Roberts, Simon Willerton, Section 3 of: On the Rozansky-Witten weight systems, Algebr. Geom. Topol. 10 (2010) 1455-1519 (arXiv:math/0602653)
See also
-
Vladimir Hinich, Arkady Vaintrob, Cyclic operads and algebra of chord diagrams, Sel. math., New ser. (2002) 8: 237 (arXiv:math/0005197)
-
Alexander Schrijver, On Lie algebra weight systems for 3-graphs (arXiv:1412.6923)
For
For the special linear Lie algebra
-
Sergei Chmutov, Alexander Varchenko, Remarks on the Vassiliev knot invariants coming from , Topology 36 (1), 153-178, 1997 (doi:10.1016/0040-9383(95)00071-2)
-
S. Tyurina, Alexander Varchenko, A remark on approximation of the Kontsevich integral of the unknot, Journal of Mathematical Sciences 131 (2005) 5270–5274 (arXiv:math/0111201, doi:10.1007/s10958-005-0399-1)
-
E. Kulakova, S. Lando, T. Mukhutdinova, G. Rybnikov, On a weight system conjecturally related to , European Journal of Combinatorics Volume 41, October 2014, Pages 266-277 (arXiv:1307.4933)
For
For the special linear Lie algebra for all :
-
Fumikazu Nagasato, A Diagrammatic Construction of the -Weight System, Interdisciplinary Information Sciences, 9 1 (2003) 43-51 (doi:10.4036/iis.2003.43)
-
Fumikazu Nagasato, An Exposition of the -Weight System, Journal of Lie Theory 17 (2007), No. 2, 263–281, Heldermann Verlag 2007 (jlt:17014)
For
For the super Lie algebra :
- José Figueroa-O’Farrill, Takashi Kimura, Arkady Vaintrob, The universal Vassiliev invariant for the Lie superalgebra , Commun. Math. Phys. 185 (1997) 93-127 (arXiv:q-alg/9602014)
Further discussion
Relation of the colored Jones polynomial to Lie algebra weight systems on chord diagrams:
- Dror Bar-Natan, Stavros Garoufalidis, On the Melvin–Morton–Rozansky conjecture, Invent math (1996) 125: 103 (doi:10.1007/s002220050070, pdf)
On the logical equivalence between the four-colour theorem and a statement about transition from the small N limit to the large N limit for Lie algebra weight systems on Jacobi diagrams via the 't Hooft double line construction:
- Dror Bar-Natan, Lie Algebras and the Four Color Theorem, Combinatorica 17-1(1997) 43–52 (arXiv:q-alg/9606016, doi:10.1007/BF01196130)
Chord diagrams and weight systems in Physics
The following is a list of references that involve (weight systems on) chord diagrams/Jacobi diagrams in physics:
-
In quantum many body models for for holographic brane/bulk correspondence:
For a unifying perspective (via Hypothesis H) and further pointers, see:
-
Hisham Sati, Urs Schreiber, Differential Cohomotopy implies intersecting brane observables, Adv. Theor. Math. Phys. 26 4 (2022) [arXiv:1912.10425]
-
David Corfield, Hisham Sati, Urs Schreiber: Fundamental weight systems are quantum states Lett. Math. Phys. 113 112 (2023) [arXiv:2105.02871, doi:10.1007/s11005-023-01725-4]
-
Carlo Collari, A note on weight systems which are quantum states, Can. Math. Bull. (2023) arXiv:2210.05399, doi:10.4153/S0008439523000206
Review:
- Carlo Collari, Weight systems which are quantum states, talk at QFT and Cobordism, CQTS (Mar 2023) web, pdf
In Chern-Simons theory
Since weight systems are the associated graded of Vassiliev invariants, and since Vassiliev invariants are knot invariants arising as certain correlators/Feynman amplitudes of Chern-Simons theory in the presence of Wilson lines, there is a close relation between weight systems and quantum Chern-Simons theory.
Historically this is the original application of chord diagrams/Jacobi diagrams and their weight systems, see also at graph complex and Kontsevich integral.
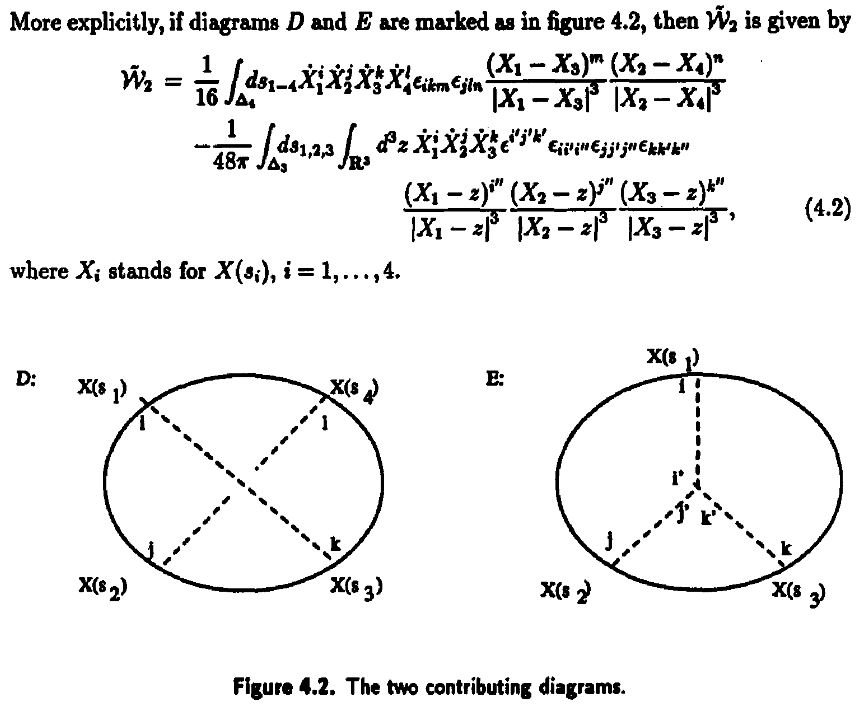
-
Dror Bar-Natan, Perturbative aspects of the Chern-Simons topological quantum field theory, thesis 1991 (spire:323500, proquest:303979053, BarNatanPerturbativeCS91.pdf)
-
Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)
-
Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arxiv:q-alg/9603010)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Algebraic structures on graph cohomology, Journal of Knot Theory and Its Ramifications, Vol. 14, No. 5 (2005) 627-640 (arXiv:math/0307218)
Reviewed in:
- Ismar Volić, Section 4 of: Configuration space integrals and the topology of knot and link spaces, Morfismos, Vol 17, no 2, 2013 (arxiv:1310.7224)
Applied to Gopakumar-Vafa duality:
- Dave Auckly, Sergiy Koshkin, Introduction to the Gopakumar-Vafa Large Duality, Geom. Topol. Monogr. 8 (2006) 195-456 (arXiv:0701568)
See also
-
Marcos Mariño, Chern-Simons theory, matrix integrals, and perturbative three-manifold invariants, Commun. Math. Phys. 253 (2004) 25-49 (arXiv:hep-th/0207096)
-
Stavros Garoufalidis, Marcos Mariño, On Chern-Simons matrix models (pdf, pdf)
For single trace operators in AdS/CFT duality
Interpretation of Lie algebra weight systems on chord diagrams as certain single trace operators, in particular in application to black hole thermodynamics
- Micha Berkooz, Prithvi Narayan, Joan Simón, Section 2.1 of Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
In , JT-gravity/SYK-model
Discussion of (Lie algebra-)weight systems on chord diagrams as SYK model single trace operators:
-
Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order , JHEP 04 (2018) 146 (arXiv:1801.02696)
-
Yiyang Jia, Jacobus J. M. Verbaarschot, Section 4 of: Large expansion of the moments and free energy of Sachdev-Ye-Kitaev model, and the enumeration of intersection graphs, JHEP 11 (2018) 031 (arXiv:1806.03271)
-
Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
following:
- László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)
which in turn follows
- Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

With emphasis on the holographic content:
-
Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)
-
Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large Double-Scaled SYK, 2019 (pdf)
-
Micha Berkooz, Mikhail Isachenkov, Prithvi Narayan, Vladimir Narovlansky, Quantum groups, non-commutative , and chords in the double-scaled SYK model [arXiv:2212.13668]
-
Herman Verlinde, Double-scaled SYK, Chords and de Sitter Gravity [arXiv:2402.00635]
-
Micha Berkooz, Nadav Brukner, Yiyang Jia, Ohad Mamroud, A Path Integral for Chord Diagrams and Chaotic-Integrable Transitions in Double Scaled SYK [arXiv:2403.05980]
and specifically in relation, under AdS2/CFT1, to Jackiw-Teitelboim gravity:
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)
-
Henry W. Lin, The bulk Hilbert space of double scaled SYK, J. High Energ. Phys. 2022 60 (2022) arXiv:2208.07032, doi:10.1007/JHEP11(2022)060
-
Henry W. Lin, Douglas Stanford, A symmetry algebra in double-scaled SYK arXiv:2307.15725
In D/D-brane intersections
Discussion of weight systems on chord diagrams as single trace observables for the non-abelian DBI action on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):
-
Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)
-
Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)
-
Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)
-
Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)
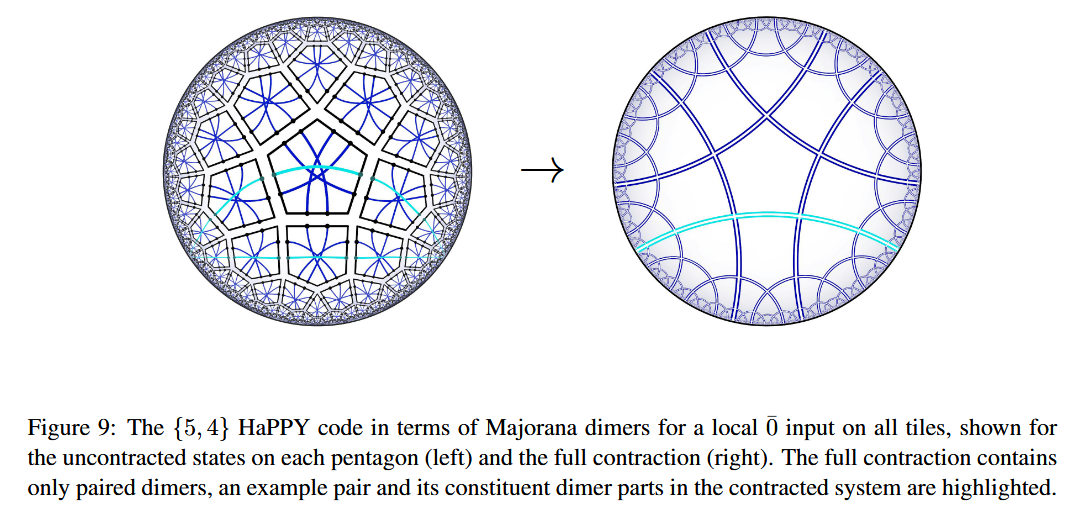
As codes for holographic entanglement entropy
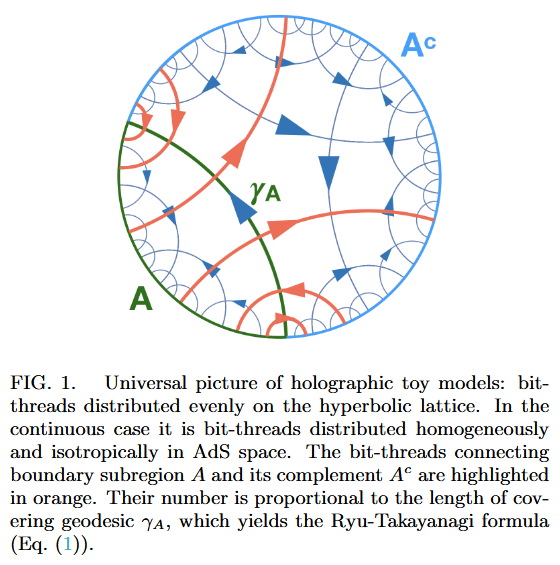
Chord diagrams encoding Majorana dimer codes and other quantum error correcting codes via tensor networks exhibiting holographic entanglement entropy:
-
Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting code, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
-
Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)
For Dyson-Schwinger equations
Discussion of round chord diagrams organizing Dyson-Schwinger equations:
-
Nicolas Marie, Karen Yeats, A chord diagram expansion coming from some Dyson-Schwinger equations, Communications in Number Theory and Physics, 7(2):251291, 2013 (arXiv:1210.5457)
-
Markus Hihn, Karen Yeats, Generalized chord diagram expansions of Dyson-Schwinger equations, Ann. Inst. Henri Poincar Comb. Phys. Interact. 6 no 4:573-605 (arXiv:1602.02550)
-
Paul-Hermann Balduf, Amelia Cantwell, Kurusch Ebrahimi-Fard, Lukas Nabergall, Nicholas Olson-Harris, Karen Yeats, Tubings, chord diagrams, and Dyson-Schwinger equations [arXiv:2302.02019]
Review in:
- Ali Assem Mahmoud, Section 3 of: On the Enumerative Structures in Quantum Field Theory (arXiv:2008.11661)
Last revised on May 7, 2021 at 02:58:28. See the history of this page for a list of all contributions to it.