nLab stringy weight systems span classical Lie algebra weight systems

Idea

The linear span of the image of stringy weight systems inside weight systems on Jacobi diagrams (under passage to the point particle limit) coincides with that of Lie algebra weight systems coming from metric Lie representations of the general linear Lie algebras $\mathfrak{gl}(n)$ and special orthogonal Lie algebras $\mathfrak{so}(n)$, which in turn contains also the Lie algebra weight systems coming from abelian and symplectic Lie algebras $\mathfrak{sp}(n)$.

Bar-Natan 95, Theorem 11

Ingredients

Details

Given any ground field $\mathbb{F}$, consider

(1)$$Span\big( MarkedSurfaces_{/\sim} \big) \;\in\; Vect$$

the linear span of the set of diffeomorphism classes of surfaces with boundary equipped with a finite number of chosen oriented points on their boundary, at least one on each connected component (Bar-Natan 95, Def. 1.12).

A stringy weight system is a linear map from this space to the ground field, hence the space of stringy weight systems is the dual vector space

(2)$$\mathcal{S} \;\coloneqq\; \Big( Span\big( MarkedSurfaces_{/\sim} \big) \Big)^\ast \,.$$

Of course a linear function $Span\big( MarkedSurfaces_{/\sim}\big) \to \mathbb{F}$ is equivalently a plain function $MarkedSurfaces \to \mathbb{F}$, but for the following construction it is necessary to consider formal linear combinations of marked surfaces:

The 't Hooft double line construction constitutes a linear map from the linear span of Jacobi diagrams modulo STU-relations to the linear span of marked surfaces (1)

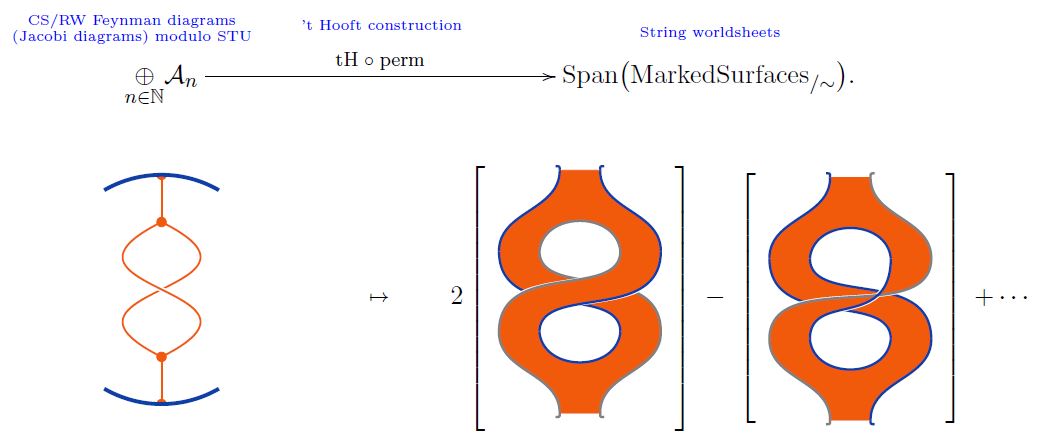
(Bar-Natan 95, Theorem 10 with Theorem 8)

graphics from Sati-Schreiber 19c

Under passage to dual vector spaces this yields a linear map

(3)$$\mathcal{S} \overset{ (tH \,\circ\, perm)^\ast }{\longrightarrow} \underset{n \in \mathbb{N}}{\prod} \big( \mathcal{W}^n \big)$$

from stringy weight systems (2) to ordinary weight systems. This may be regarded as the point particle limit of stringy weight systems.

Statement

Remark

(stringy weight systems span classical Lie algebra weight systems)

The image of the vector space (2) of stringy weight systems under the point particle limit map (3) inside the space of ordinary weight systems coincides with the direct sum of the linear span of Lie algebra weight systems for the general linear Lie algebras $\mathfrak{gl}(N)$ and the special orthogonal Lie algebras $\mathfrak{so}(N)$, and contains that of symplectic Lie algebras $\mathfrak{sp}(N)$:

(Bar-Natan 95, Theorem 11)

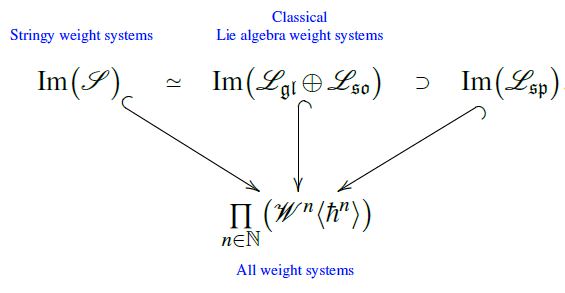
graphics from Sati-Schreiber 19c

Related theorems

Facts about chord diagrams and their weight systems:

• chord diagrams modulo 4T are Jacobi diagrams modulo STU

• weight systems are the associated graded objects of Vassiliev invariants

• weight systems are cohomology of loop space of configuration space

• weight systems are cohomology of knot graph complex

• stringy weight systems span classical Lie algebra weight systems

• all horizontal weight systems are partitioned Lie algebra weight systems

References

• Dror Bar-Natan, p. 9 and section 6 of: On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)

See also

• Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Section 6.2.4 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)