nLab chord diagrams modulo 4T are Jacobi diagrams modulo STU
Context
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Ingredients
Consider
-
the set of chord diagrams;
-
the set of Jacobi diagrams;
Write
for the canonical injection, regarding chord diagrams as Jacobi diagrams without internal vertices, hence with all vertices on the circle.
For CRing a commutative ring, write
-
for the -linear span of chord diagrams;
-
for the linear span of Jacobi diagrams
and finally
for the respective quotient spaces by the 4T relations
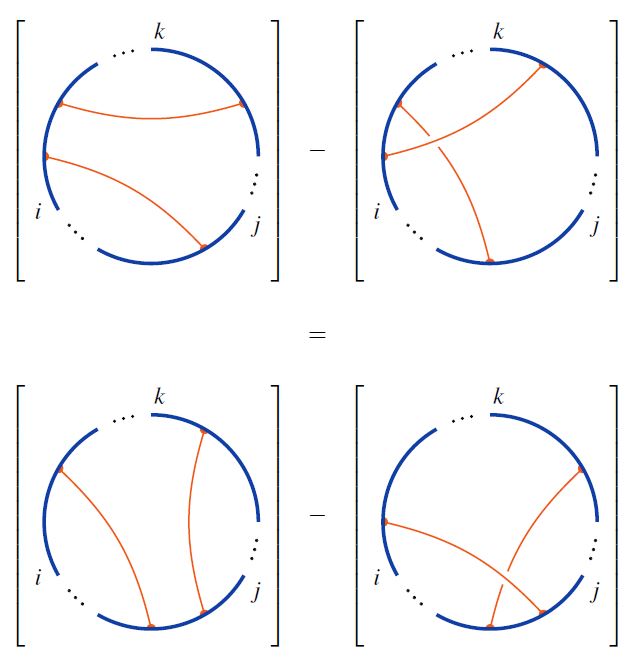
and by the STU relations
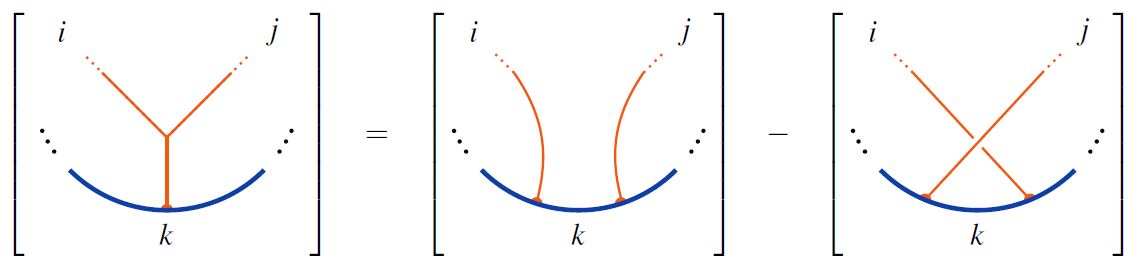
respectively.
graphics from Sati-Schreiber 19c
Statement
The linear extension of the canonical inclusion (1) descends to the quotients (2) and yields a linear isomorphism:
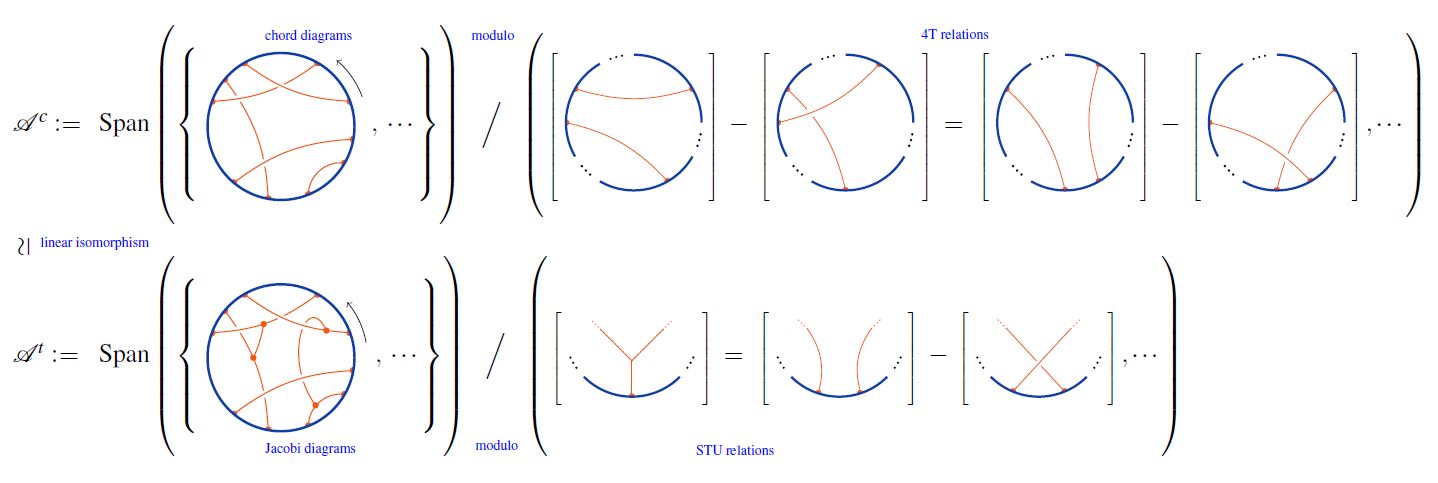
This is due to Bar-Natan 95, Theorem 6. See also Chmutov-Duzhin-Mostovoy 11, 5.3
graphics from Sati-Schreiber 19
The key step of the proof is to observe that the STU-relations imply the 4T-relations as follows:
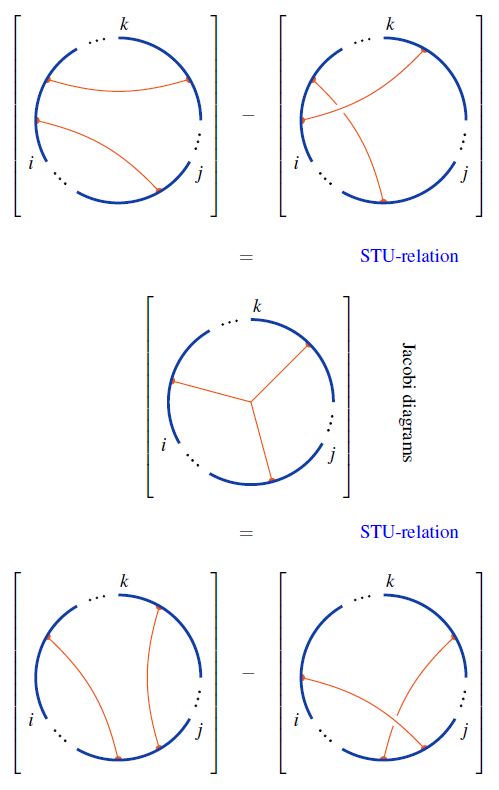
graphics from Sati-Schreiber 19c
Application
Relation to weight systems
The immediate consequence is that the space of framed weight systems , which by definition is the dual vector space to the linear span of chord diagrams modulo the 4T-relations, is equiuvalently also the dual vector space to the linear span of chord diagrams modulo the 4T-relations:
Related theorems
Facts about chord diagrams and their weight systems:
Related concepts
References
The result is due to
- Dror Bar-Natan, Theorem 6 in: On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)
Lecture notes
- Dror Bar-Natan, Alexander Stoimenow, The Fundamental Theorem of Vassiliev Invariants (arXiv:q-alg/9702009)
Textbook accounts:
- Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Section 5.3 of Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)
Last revised on April 25, 2021 at 07:17:16. See the history of this page for a list of all contributions to it.