nLab metric Lie representation

Idea

Given a Lie algebra $(\mathfrak{g}, [-,-])$ and a Lie algebra representation $\mathfrak{g} \otimes V \overset{\rho}{\to} V$, and given non-degenerate inner products, hence “metrics”, both on $\mathfrak{g}$ and on $V$, one may ask that all structure is compatible with these metrics. For the Lie algebra this means to have a metric Lie algebra and for the representation this means to have an orthogonal representation. Hence together this is an orthogonal representation of a metric Lie algebra, or metric Lie representation, for short.

Definition

The following table shows the data in a metric Lie representation equivalently

1. in category theory-notation;

2. in Penrose notation (string diagrams);

3. in index notation:

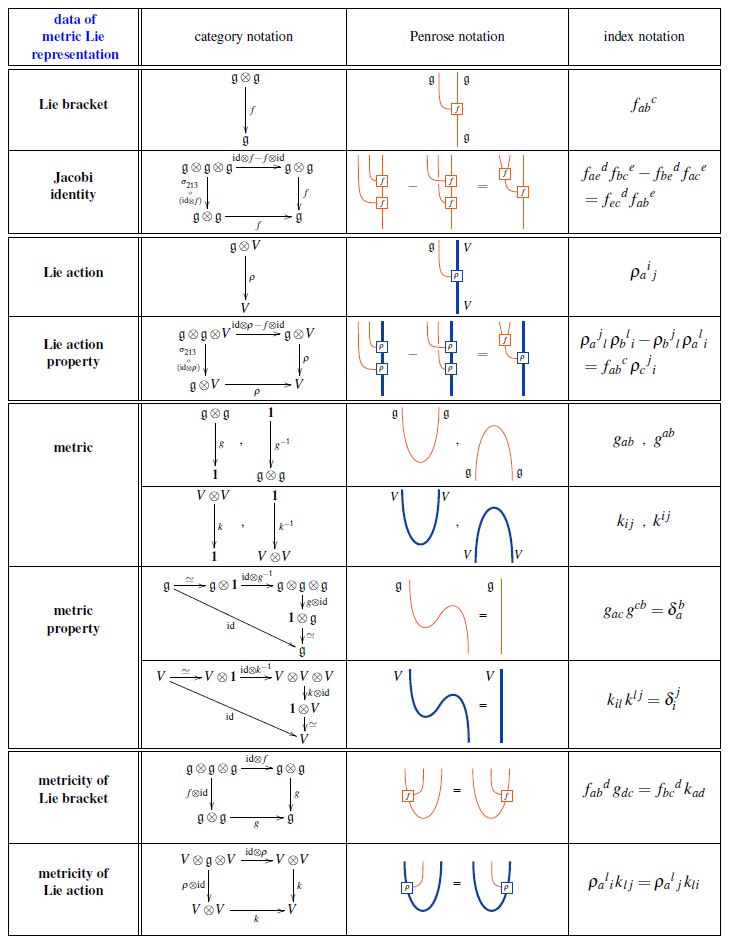
graphics from Sati-Schreiber 19c

Properties

Structures induced from metric Lie representations

The following mathematical structures are induced from the data of metric Lie representations:

• Lie algebra weight systems on (horizontal) chord diagrams;

• M2-brane 3-algebras (the Faulkner construction);

• …

See there for more.

Related concepts

• metric Lie algebra

• Lie algebra weight system

• M2-brane 3-algebra

References

On the Faulkner construction (which became known as the M2-brane 3-algebra constructed from a metric Lie representation):

• John Faulkner, On the geometry of inner ideals, Journal of Algebra, Volume 26, Issue 1, July 1973, Pages 1-9 (doi:10.1016/0021-8693(73)90032-X)