nLab fuzzy sphere
Context
Noncommutative geometry
(geometry Isbell duality algebra)
Topology
Smooth and Riemannian geometry
Algebraic geometry
Homotopy theory
Relation to physics
Spheres
Contents
Idea
A fuzzy sphere is a variant of an n-sphere in noncommutative geometry. Often the fuzzy 2-sphere is meant by default, but there are also fuzzy spheres of higher dimension.
Definition
Fuzzy 2-sphere
For , , the fuzzy 2-sphere of bits is the formal dual to the associative algebra which is the sub-algebra in the matrix algebra generated from the elements of the -dimensional complex irreducible Lie algebra representation of su(2).
We now say this more in detail:
Conventions and Normalizations
First to introduce relevant notation and to set out the proper choices of normalizations.
With the Lie algebra su(2) of SU(2), with complexification the special linear Lie algebra sl(2) (see here)
write
for a choice of linear basis such that the Lie bracket takes the form
(Here is the Levi-Civita symbol, hence is the signature of the permutation .)
Notice that the element
is a Casimir element in the universal enveloping algebra.
Let then
denote the complex -dimensional complex irreducible Lie algebra representation of su(2) (hence of ).
In the discussion of angular momentum in quantum mechanics the image
of the Casimir element (3) under the representation (4) is traditionally denoted , and the canonical linear basis for the N-dimensional representation (4) is then traditionally denoted with
hence with
This means that the eigenvalues of (5) as a function not of the angular momentum but of the dimension of the given irreducible representation are:
Algebra of functions
Write now
for the square matrices representing the generators (1) in the -dimensional complex irrep (4), suitably normalized in view of (7).
(It is here that we need the assumption , hence excluding the complex 1-dimensional trivial irrep.)
Due to the normalization, the commutation relation (2) in this representation reads
and, by (7), the image of the Casimir element (3) under this representation is the identity matrix:
Equation (9) shows that in the large N limit , the algebra generated by the becomes commutative, and (10) says that for any , the algebra generated by the satisfies the same relation as the smooth algebra on generators restricted to the actual 2-sphere of unit radius:
Integration
With the above, the volume density of the fuzzy 2-sphere scales with
In this vein, one defines the fuzzy refinement of the integral of functions over the 2-sphere, against its canonical volume form, to be given by the matrix trace, normalized as follows
With this definition the volume of the fuzzy 2-sphere of bits comes out as
This indeed goes to the volume of the actual 2-sphere in the limit :
Properties
Shape observables as weight systems on chord diagrams
We discuss how the “shape observables” on the fuzzy 2-sphere (above) are given by single trace observables which are Lie algebra weight systems on chord diagrams (following Ramgoolam-Spence-Thomas 04, McNamara-Papageorgakis 05, see McNamara 06, Section 4 for review).
For more see at weight systems on chord diagrams in physics.
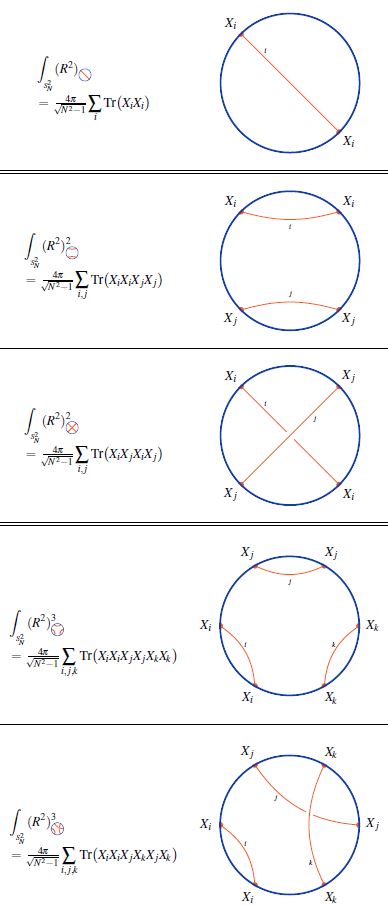
While in the commutative large N limit, all powers of the radius function are equal
for finite there is an ordering ambiguity: In fact, the number of functions on the fuzzy 2-sphere at finite that all go to the same function in the large N limit grows rapidly with .
At there is the single radius observable (10)
At there are, under the integral (11), two radius observables:
(Here we are using that under the integral/trace, a cyclic permutation of the factors in the integrand does not change the result).
Similarly for higher , where the number of possible orderings increases rapidly. The combinatorics that appears here is familiar in knot theory:
Every ordering of operators, up to cyclic permutation, in the single trace observable is encoded in a chord diagram and the value of the corresponding single trace observable is the value of the su(2)-Lie algebra weight system on this chord diagram.
from Sati-Schreiber 19c
Appearance in D-brane geometry
The fuzzy spheres appear in D-brane geometry:
-
the fuzzy funnels of Dp-D(p+2)-brane intersections have fuzzy 2-sphere slices
-
the fuzzy funnels of Dp-D(p+4)-brane intersections have fuzzy 4-sphere slices
-
the supersymmetric classical solutions of the BMN matrix model are precisely fuzzy 2-sphere configurations (BMN 02 (5.4)).
Related concepts
References
General
Review in the context of D-brane geometry, matrix models of string theory/M-theory (BFSS matrix model, BMN matrix model, IKKT matrix model):
- Badis Ydri, Review of M(atrix)-Theory, Type IIB Matrix Model and Matrix String Theory (arXiv:1708.00734), published as: Matrix Models of String Theory, IOP 2018 (ISBN:978-0-7503-1726-9)
Fuzzy 2-sphere
On the fuzzy 2-sphere:
General
The fuzzy 2-sphere was introduced in:
- John Madore, The Fuzzy sphere, Class. Quant. Grav. 9 (1992) 69-88 (spire:314358)
Discussion of the spectral Riemannian geometry of the fuzzy 2-sphere:
-
Francesco D'Andrea, Fedele Lizzi, Joseph Várilly, Metric Properties of the Fuzzy Sphere, Lett. Math. Phys.103 (2013), 183-205 (arXiv:1209.0108)
-
Anwesha Chakraborty, Partha Nandi, Biswajit Chakraborty, A note on spectral triple with real structure on fuzzy sphere (arXiv:2111.03012)
In the context of the IKKT matrix model:
- Harold Steinacker, Non-commutative geometry and matrix models, PoS QGQGS2011 (2011) 004 (arXiv:1109.5521)
See also:
- Wikipedia, Fuzzy sphere
Observables via weight systems on chord diagrams
Relation of Dp-D(p+2)-brane bound states (hence Yang-Mills monopoles) to su(2)-Lie algebra weight systems on chord diagrams computing radii averages of fuzzy spheres:
-
Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)
-
Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)
-
Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)
-
Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)
Fuzzy 3-sphere
The fuzzy 3-sphere was first discussed (in the context of D0-brane-systems) in
- Z. Guralnik, Sanyaje Ramgoolam, On the Polarization of Unstable D0-Branes into Non-Commutative Odd Spheres, JHEP 0102:032, 2001 (arXiv:hep-th/0101001)
Discussion in the context of M2-M5-brane bound states/E-strings:
- Anirban Basu, Jeffrey Harvey, The M2-M5 Brane System and a Generalized Nahm’s Equation, Nucl.Phys. B713 (2005) 136-150 (arXiv:hep-th/0412310)
See also:
- Samuel Kováčik, Juraj Tekel, Fuzzy Onion as a Matrix Model [arXiv:2309.00576]
Fuzzy 4-sphere
The fuzzy 4-sphere:
-
Harald Grosse, Ctirad Klimcik, P. Presnajder, On Finite 4D Quantum Field Theory in Non-Commutative Geometry, Commun. Math. Phys.180:429-438, 1996 (arXiv:hep-th/9602115)
-
Judith Castelino, Sangmin Lee, Washington Taylor, Longitudinal 5-branes as 4-spheres in Matrix theory, Nucl. Phys. B526:334-350, 1998 (arXiv:hep-th/9712105)
(via D5-branes)
Fuzzy 6-sphere and higher
The fuzzy 6-sphere and higher:
-
Sanjaye Ramgoolam, Section 5 of: On spherical harmonics for fuzzy spheres in diverse dimensions, Nucl. Phys. B610: 461-488, 2001 (arXiv:hep-th/0105006)
-
Yusuke Kimura, On Higher Dimensional Fuzzy Spherical Branes, Nucl. Phys. B664 (2003) 512-530 (arXiv:hep-th/0301055)
-
Francesco Pisacane, -equivariant fuzzy spheres (arXiv:2002.01901)
See also:
- Denjoe O’Connor, Brian P. Dolan, Exceptional fuzzy spaces and octonions [arXiv:2210.14754]
Last revised on September 4, 2023 at 08:16:10. See the history of this page for a list of all contributions to it.