nLab 7-sphere
Context
Spheres
Contents
Idea
This is one of the parallelizable spheres, as such corresponds to the octonions among the division algebras, being the manifold of unit octonions, and is the only one of these which does not carry (Lie) group structure but just Moufang loop structure.
Properties
Quaternionic Hopf fibration
The 7-sphere participates in the quaternionic Hopf fibration, the analog of the complex Hopf fibration with the field of complex numbers replaced by the division ring of quaternions or Hamiltonian numbers .
Here the idea is that can be construed as , with mapping to as an element in the projective line , with each fiber a torsor parametrized by quaternionic scalars of unit norm (so ). This canonical -bundle (or -bundle) is classified by a map .
Coset space realizations
Proposition
(coset space of Spin(7) by G2 is 7-sphere)
Consider the canonical action of Spin(7) on the unit sphere in (the 7-sphere),
-
This action is is transitive;
-
the stabilizer group of any point on is G2;
-
all G2-subgroups of Spin(7) arise this way, and are all conjugate to each other.
Hence the coset space of Spin(7) by G2 is the 7-sphere
(e.g Varadarajan 01, Theorem 3)
Other coset realizations of the usual differentiable 7-sphere (Choquet-Bruhat, DeWitt-Morette 00, p. 288):
These three coset realizations of ‘squashed’ 7-spheres together with a fourth
- ,
the realization of the ‘round’ 7-sphere, may be seen jointly as resulting from the 8-dimensional representations of even Clifford algebras in 5, 6, 7, and 8 dimensions (see Baez) and as such related to the four normed division algebras. See also Choquet-Bruhat+DeWitt-Morette00, pp. 263-274.
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G2 is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G2/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
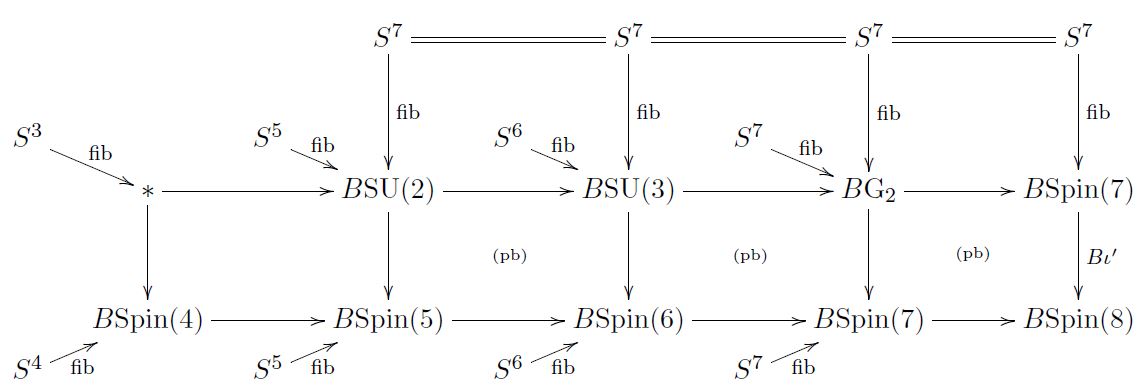
(from FSS 19, 3.4)
The following gives an exotic 7-sphere:
Exotic 7-spheres
A celebrated result of Milnor is that admits exotic smooth structures (see at exotic 7-sphere), i.e., there are smooth manifold structures on the topological manifold that are not diffeomorphic to the standard smooth structure on . More structurally, considering smooth structures up to oriented diffeomorphism, the different smooth structures form a monoid under a (suitable) operation of connected sum, and this monoid is isomorphic to the cyclic group . With the notable possible exception of (where the question of existence of exotic 4-spheres is wide open), exotic spheres first occur in dimension . This phenomenon is connected to the h-cobordism theorem (the monoid of smooth structures is identified with the monoid of h-cobordism classes of oriented homotopy spheres).
One explicit construction of the smooth structures is given as follows (see Milnor 1968). Let be the algebraic variety in defined by the equation
and a sphere of small radius centered at the origin. Then each of the smooth structures on is represented by an intersection , as ranges from to . These manifolds sometimes go by the name Brieskorn manifolds or Brieskorn spheres or Milnor spheres.
-structure
Let be the associative 3-form and let
be given by
(where denotes the canonical coordinate on the first factor of and is pulled back along the projection to ) .
By construction this is its own Hodge dual
This implies that as we restrict to
then there is a unique 3-form
on the 7-sphere such that
This 3-form defines a G2-structure on . It is nearly parallel in that
(e.g. Lotay 12, def.2.4)
Related concepts
References
-
Martin Cederwall, Christian R. Preitschopf, The Seven-sphere and its Kac-Moody Algebra, Commun. Math. Phys. 167 (1995) 373-394 (arXiv:hep-th/9309030)
-
Takeshi Ôno, On the Hopf fibration over , Nagoya Math. J. Volume 59 (1975), 59-64. (Euclid)
Relation to the Milnor fibration:
- Kenneth Intriligator, Hans Jockers, Peter Mayr, David Morrison, M. Ronen Plesser, Conifold Transitions in M-theory on Calabi-Yau Fourfolds with Background Fluxes, Adv.Theor.Math.Phys. 17 (2013) 601-699 (arXiv:1203.6662)
An ADE classification of finite subgroups of acting freely on (see at group action on an n-sphere) such that the quotient is spin and has at least four Killing spinors (see also at ABJM model) is in
-
Paul de Medeiros, José Figueroa-O'Farrill, Sunil Gadhia, Elena Méndez-Escobar, Half-BPS quotients in M-theory: ADE with a twist, JHEP 0910:038,2009 (arXiv:0909.0163, pdf slides)
-
Paul de Medeiros, José Figueroa-O'Farrill, Half-BPS M2-brane orbifolds (arXiv:1007.4761)
Discussion of subgroups:
- Veeravalli Varadarajan, Spin(7)-subgroups of SO(8) and Spin(8), Expositiones Mathematicae, 19 (2001): 163-177 (pdf)
Discussion of exotic smooth structures on 7-spheres includes
- Wikipedia, Exotic sphere, link.
The explicit construction of exotic 7-spheres by intersecting algebraic varieties with spheres is described in
- John Milnor, “Singular points of complex hypersurfaces” , Princeton Univ. Press (1968).
Discussion of (nearly) G2-structures on and calibrated submanifolds includes
- Jason Lotay, Associative Submanifolds of the 7-Sphere, Proc. London Math. Soc. (2012) 105 (6): 1183-1214 (arXiv:1006.0361, talk slides)
On coset-realizations:
-
Linus Kramer, Octonion Hermitian quadrangles, Bull. Belg. Math. Soc. Simon Stevin Volume 5, Number 2/3 (1998), 353-362 (euclid:1103409015)
-
Yvonne Choquet-Bruhat, Cécile DeWitt-Morette, Analysis, manifolds and physics, Part II, North Holland (1982, 2001) ISBN:9780444860170
-
M. A. Awada, Mike Duff, Christopher Pope, Supergravity Breaks Down to , Phys. Rev. Lett. 50, 294 – Published 31 January 1983 (doi:10.1103/PhysRevLett.50.294)
-
Mike Duff, Bengt Nilsson, Christopher Pope, Spontaneous Supersymmetry Breaking by the Squashed Seven-Sphere, Phys. Rev. Lett. 50, 2043 – Published 27 June 1983; Erratum Phys. Rev. Lett. 51, 846 (doi:10.1103/PhysRevLett.50.2043)
-
John Baez, Rotations in the 7th Dimension, (blog post), and TWF 195, (webpage)
Last revised on June 4, 2022 at 17:39:42. See the history of this page for a list of all contributions to it.