Schreiber Equivariant Cohomotopy implies orientifold tadpole cancellation
An article that we have written:
-
Equivariant Cohomotopy implies orientifold tadpole cancellation
Journal of Geometry and Physics
156 (2020) 103775
download article:
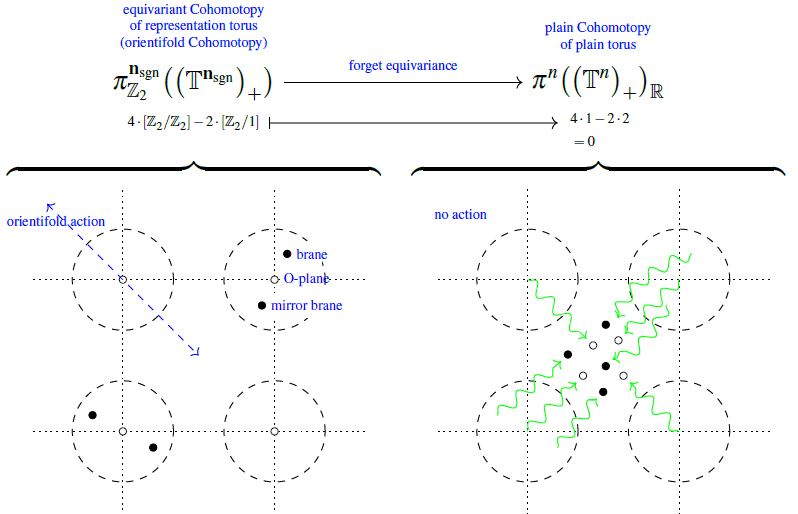
Abstract There are fundamental open problems in the precise global nature of RR-field tadpole cancellation conditions in string theory. Moreover, the non-perturbative lift as M5/MO5-anomaly cancellation in M-theory had been based on indirect plausibility arguments, lacking a microscopic underpinning in M-brane charge quantization. We provide a framework for answering these questions, crucial not only for mathematical consistency but also for phenomenological accuracy of string theory, by formulating the M-theory C-field on flat M-orientifolds in the generalized cohomology theory called Equivariant Cohomotopy. This builds on our previous results for smooth but curved spacetimes, showing in that setting that charge quantization in twisted Cohomotopy (“Hypothesis H”) rigorously implies a list of expected anomaly cancellation conditions. Here we further expand this list by proving that brane charge quantization in unstable equivariant Cohomotopy implies the anomaly cancellation conditions for M-branes and D-branes on flat orbi-orientifolds. For this we (a) use an unstable refinement of the equivariant Hopf-tom Dieck theorem to derive local/twisted tadpole cancellation, and (b) the lift to super-differential cohomology to establish global/untwisted tadpole cancellation. Throughout, we use (c) the unstable Pontrjagin-Thom theorem to identify the brane/O-plane configurations encoded in equivariant Cohomotopy and (d) the Boardman homomorphism to equivariant K-theory to identify Chan-Paton representations of D-brane charge. We find that unstable equivariant Cohomotopy, but not its image in equivariant K-theory, distinguishes D-brane charge from the finite set of types of O-plane charges.
Based on:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
The rational higher structure of M-theory
Proceedings of the LMS-EPSRC Durham Symposium:
Higher Structures in M-Theory, August 2018,
Fortschritte der Physik, 2019
-
John Huerta, Hisham Sati, Urs Schreiber,
Real ADE-equivariant (co)homotopy and Super M-branes
Communications in Mathematical Physics (2019)
-
Simon Burton, Hisham Sati, Urs Schreiber:
Lift of fractional D-brane charge to equivariant Cohomotopy theory
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Followup:
-
Differential Cohomotopy implies intersecting brane observables
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Twisted Cohomotopy implies twisted String structure on M5-branes
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Twistorial Cohomotopy implies Green-Schwarz anomaly cancellation
Related talk notes:
-
Equivariant Cohomotopy of toroidal orbifolds
talk at Prof. Sadok Kallel‘s group seminar
AUS Sharjah, 2019
-
The Higher Structure of 11d Supergravity
talk at Souriau 2019
IHP Paris, May 2019
-
Equivariant Cohomotopy and Branes
talk at String and M-Theory: The New Geometry of the 21st Century
NUS Singapore, 2018
-
Super p-Brane Theory emerging from Super Homotopy Theory
talk at StringMath2017,
Hamburg, 2017
-
Twisted Cohomotopy implies M-theory anomaly cancellation
presentation at Strings2019
Brussels, 2019
-
Equivariant Stable Cohomotopy and Branes
talk at Geometry, Topology and Physics
NYU Abu Dhabi, 2018
-
Equivariant cohomology of M2/M5-branes
talk at Seminar on Higher Structures
MPI Bonn, 2016
Last revised on November 23, 2021 at 18:28:17. See the history of this page for a list of all contributions to it.