Schreiber Equivariant homotopy and super M-branes

An article that we have written:

---

• John Huerta, Hisham Sati, Urs Schreiber,

  
  

  Real ADE-equivariant (co)homotopy and Super M-branes

  
  

  Communications in Mathematical Physics 371 (2019) 425

  
  

  download:

  • doi:10.1007/s00220-019-03442-3

  • arXiv:1805.05987

  • pdf

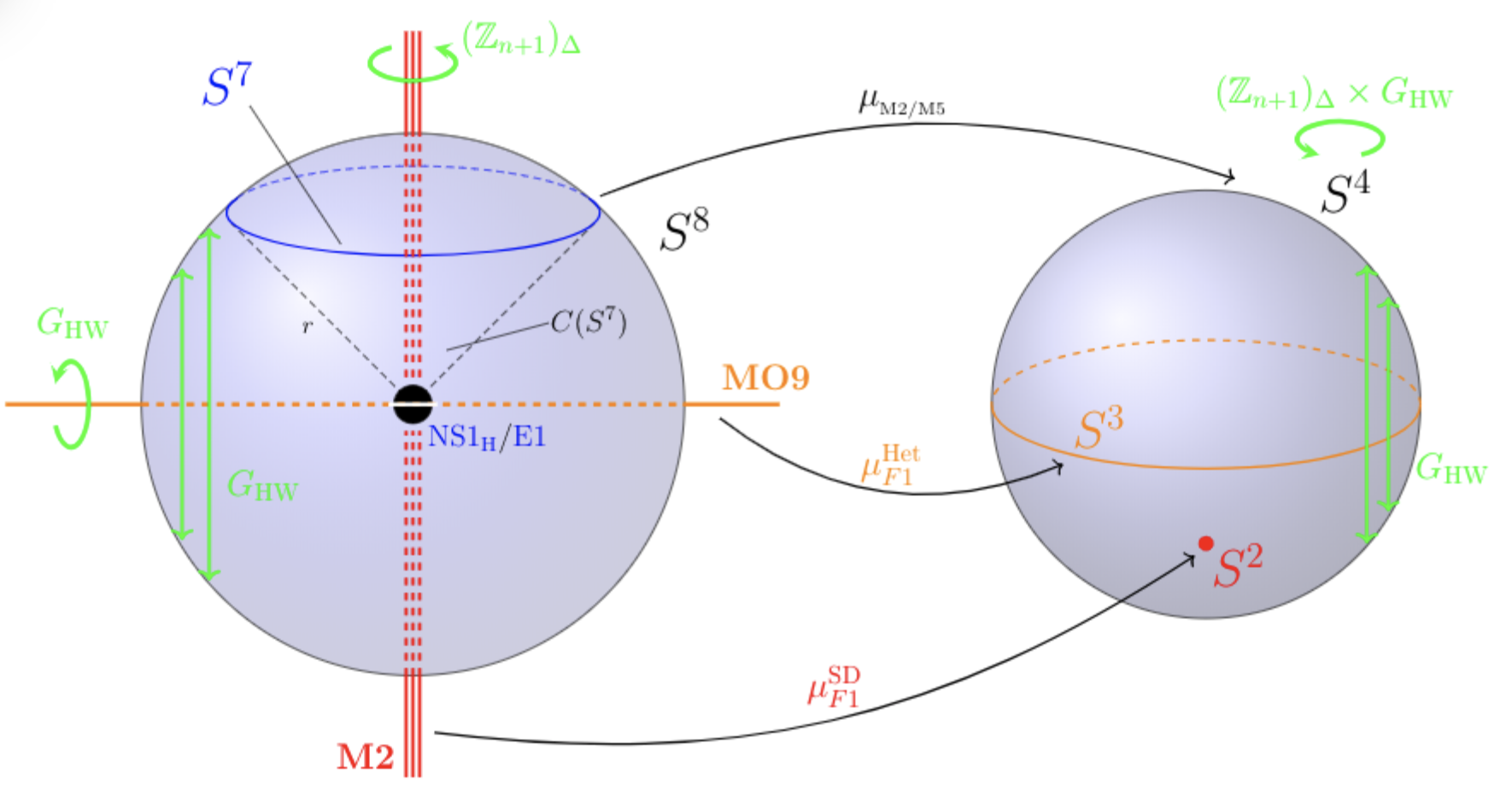
Abstract: A key open problem in M-theory is the identification of the degrees of freedom that are expected to be hidden at ADE-singularities in spacetime. Comparison with the classification of D-branes by K-theory suggests that the answer must come from the right choice of generalized cohomology theory for M-branes. Here we show that real equivariant cohomotopy on superspaces is a consistent such choice, at least rationally. After explaining this new approach, we demonstrate how to use Elmendorf's theorem in equivariant homotopy theory to reveal ADE-singularities as part of the data of equivariant 4-sphere-valued super-cocycles on 11d super-spacetime. We classify these super-cocycles and find a detailed black brane-scan that enhances the entries of the old brane scan to cascades of fundamental brane super-cocycles on strata of intersecting black M-brane species. At each stage the full Green-Schwarz action functional for the given fundamental brane species appears, as the datum associated to the morphisms in the orbit category.

---

$\,$

Related Talk notes:

• Equivariant cohomology of M2/M5-branes

• Structured Homotopy Theory from String Theory (pdf)

• Equivariant Stable Cohomotopy and Branes

Related articles:

• Gauge enhancement of Super M-Branes

• Super Lie n-algebra extensions, higher WZW models and super p-branes

• The WZW term of the M5-brane

• Rational sphere valued supercocycles in M-theory

• T-Duality from super Lie n-algebra cocycles for super p-branes

• Higher T-duality of super M-branes

• M-Theory from the Superpoint

all summed up in

• The rational higher structure of M-theory.

and further developed in

• Twisted Cohomotopy implies M-theory anomaly cancellation

• Equivariant Cohomotopy implies orientifold tadpole cancellation

See also

• Hypothesis H

• The image of the Burnside ring in the Representation ring

• Cobordisms of global quotient orbifolds and an equivariant Pontrjagin-Thom construction

$\,$