Schreiber Super-exceptional embedding construction of the M5-brane
An article that we have written:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Super-exceptional geometry: Origin of heterotic M-theory and super-exceptional embedding construction of M5
Journal of High Energy Physics 2020, 107 (2020).
download:
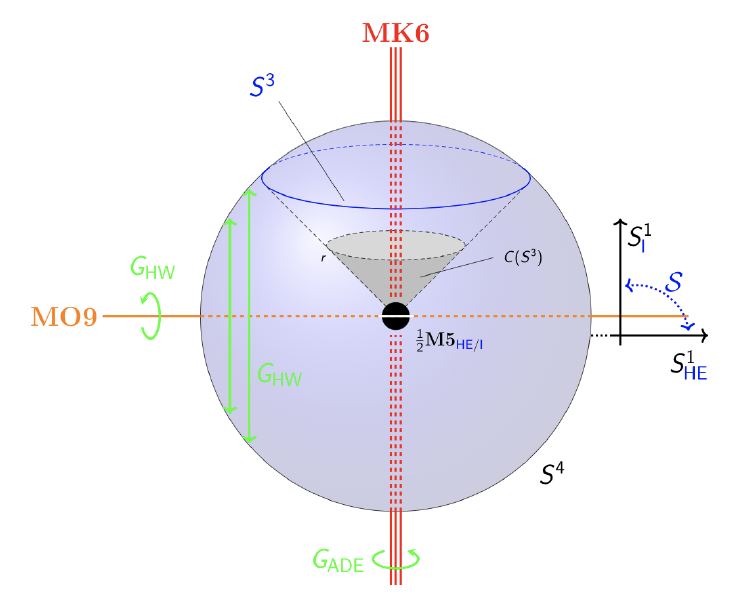
Abstract. The Green-Schwarz-type action functional for the super-membrane in 11d, i.e. for the fundamental M2-brane sigma model, turns out to elegantly arise as the supersymmetric trivialization of the C-field super-space 4-cocycle restricted from 11d-superspace to the M2 brane’s super-worldvolume. This is known as the “super-embedding construction”. An analogous construction of the M5-brane’s GS sigma-model action had remained an open problem. Here we present a result which shows that the M5-brane action, too, does arise from a super-embedding construction – but after first passing from plain 11d superspace to super-exceptional superspace.

From inspection of the resulting 5d super Yang-Mills Lagrangian we find that the extra fermion field appearing in super-exceptional M-geometry, whose physical interpretation had remained open, is the M-theoretic avatar of the gaugino field on the heterotic MO9-planes.
Based on:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber
The rational higher structure of M-theory
Proceedings of the LMS-EPSRC Durham Symposium:
Higher Structures in M-Theory, August 2018
Fortschritte der Physik, 2019
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber
Higher T-duality of super M-branes
Higher T-duality in M-theory via local supersymmetry
Physics Letters B Volume 781
10 June 2018, Pages 694-698
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Twisted Cohomotopy implies level quantization of the full 6d Wess-Zumino-term of the M5-brane
Followup:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber
Super-exceptional M5-brane model – Emergence of SU(2)-flavor sector
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
Twisted Cohomotopy implies twisted String structure on M5-branes
Related talks:
-
Super p-Brane Theory emerging from Super Homotopy Theory
talk at StringMath2017
Hamburg 2017
-
Equivariant Cohomotopy and Branes
talk at String and M-Theory: The New Geometry of the 21st Century
Singapore 2018
-
The rational higher structure of M-theory
talk at Higher Structures in M-Theory
Durham 2018
-
The Higher Structure of 11d Supergravity
talk at Souriau 2019
Paris 2019
-
Twisted Cohomotopy implies M-theory anomaly cancellation
Brussels 2019
Last revised on October 3, 2020 at 07:37:11. See the history of this page for a list of all contributions to it.