nLab Hopf invariant

Definition

In ordinary cohomology

For $n \in \mathbb{N}$ with $n \gt 1$, consider continuous functions between spheres of the form

(1)$$f \;\colon\; S^{2n-1} \longrightarrow S^n \,.$$

The homotopy cofiber of $f$ (the attaching space induced by $f$)

$$C_f \;\coloneqq\; S^n \underset{S^{2n-1}}{\cup} D^{2n}$$

has ordinary cohomology

$$H^k(C_f, \mathbb{Z}) \simeq \left\{ \array{ \mathbb{Z} & for\; k = n, 2n; \\ 0 & otherwise } \right. \,.$$

Hence for $\alpha_n, \beta_{2n}$ generators of the cohomology groups in degree $n$ and $2n$ (unique up to choice of sign), respectively, there exists an integer $HI(f)$ which expresses the cup product square of $\alpha_n$ as a multiple of $\beta_{2n}$:

(2)$$\alpha_n \cup \alpha_n \;=\; HI(f) \cdot \beta_{2n} \,.$$

This integer $HI(f) \in \mathbb{Z}$ is called the Hopf invariant of $f$ (e.g. Mosher-Tangora 86, p. 33).

This depends on the choices made only up to sign. In particular it has a well-defined mod-2 reduction image $[HI(f)] \in \mathbb{F}_2 = \mathbb{Z}/2\mathbb{Z}$ (in Z/2), and as such it is the Steenrod square

$$[HI(f)] \cdot (-) \;\colon\; \mathbb{F}_2 \;\simeq\; H^n \big( C_f; \, \mathbb{F}_2 \big) \stackrel{Sq^n}{\longrightarrow} H^{2n} \big( C_f; \, \mathbb{F}_2 \big) \;\simeq\; \mathbb{F}_2 \,.$$

In generalized cohomology

Here is a more abstract picture of the Hopf invariant in abstract homotopy theory (following SS21):

Let $E$ be a multiplicative cohomology theory, assumed to vanish in degree $2n - 1$

(3)$$\widetilde E \big( S^{2n-1} \big) \,\simeq\, \pi_{2n-1}(E) \,\simeq\, 0 \,.$$

We write $E_n \;\coloneqq\; \Omega^\infty \Sigma^n E$ for its classifying spaces, hence for the component spaces of its representing spectrum.

(For the case of ordinary cohomology $E = H \mathbb{Z}$ we have $E_n \,\simeq\, K(\mathbb{Z},n)$ an Eilenberg-MacLane space.)

Now let

$$S^{2n-1} \overset{f}{\longrightarrow} S^n$$

be a map (1). Then its $E$-Hopf invariant “is” the following homotopy pasting diagram of pointed homotopy types (see also at e-invariant is Todd class of cobounding (U,fr)-manifold):

from SS21

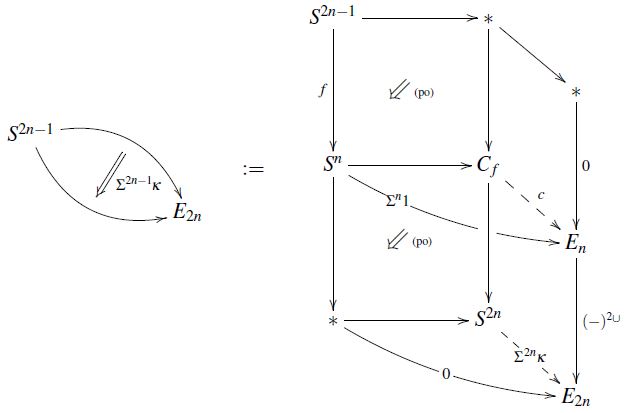
• the top square is defined to be a homotopy pushout, exhibiting the attaching space $C_f$;

• the total rectangle is defined to be a homotopy pushout, exhibiting the suspension of $S^{2n-1}$ to $S^{2n}$;

• the bottom square is hence a homotopy pushout by the pasting law;

• by assumption (3) the restriction of $\Sigma^{2n} 1$ to $S^{2n-1}$ trivializes, exhibited by a choice of homotopy filling the full top part of the diagram; and by the universal property of the top homotopy-pushout this corresponds equivalently to the dashed morphism $c$;

• the restriction of the cup square cohomology operation on $c$ to $S^n$ trivializes: $c$ factors through the $n$ component space of the connective cover $E\langle 0\rangle$, whence its cup square (by the discussion at connective cover – For ring spectra) factors through the $2n$-connective $2n$th component space of the same connective cover (as in a standard argument in complex oriented cohomology theory, e.g. Lurie, Lec. 4. Exmpl. 8, or see Conner-Floyd 66, Part I, Cor. 7.2):

• This yields the homotopy filling the full bottom part of the diagram above; and by the universal property of the bottom homotopy-pushout this corresponds equivalently to a dashed morphism $S^{2n} \to E_{2n}$, labeled by some class

  $$\kappa \,\in\, \pi_0(E) \,\simeq\, \widetilde E(S^0) \overset{\Sigma^{2n}}{\longrightarrow} \widetilde E(S^{2n}) \, = \, \big[ S^{2n} \longrightarrow E_{2n} \big] \,;$$

• finally, by the homotopy-pushout property of the total rectangle, this class $\kappa$ also labels the total homotopy filling the full diagram.

We see that:

• for $E = H \mathbb{Z}$ being ordinary cohomology, $\kappa \,\in\, \mathbb{Z}$ is the traditional Hopf invariant as discussed above;

• for $E = KU$ being complex topological K-theory, $\kappa \,\in\, \mathbb{Z}$ is the Hopf invariant in K-theory as used in Adams-Atiyah 66.

In the case that the map $f$ is one the classical Hopf fibrations, the attaching space above is a projective space (by the discussion at cell structure of projective spaces) and the choice of homotopy $c$ is the choice of an orientation in $E$-cohomology theory to second stage. Specifically:

from SS21

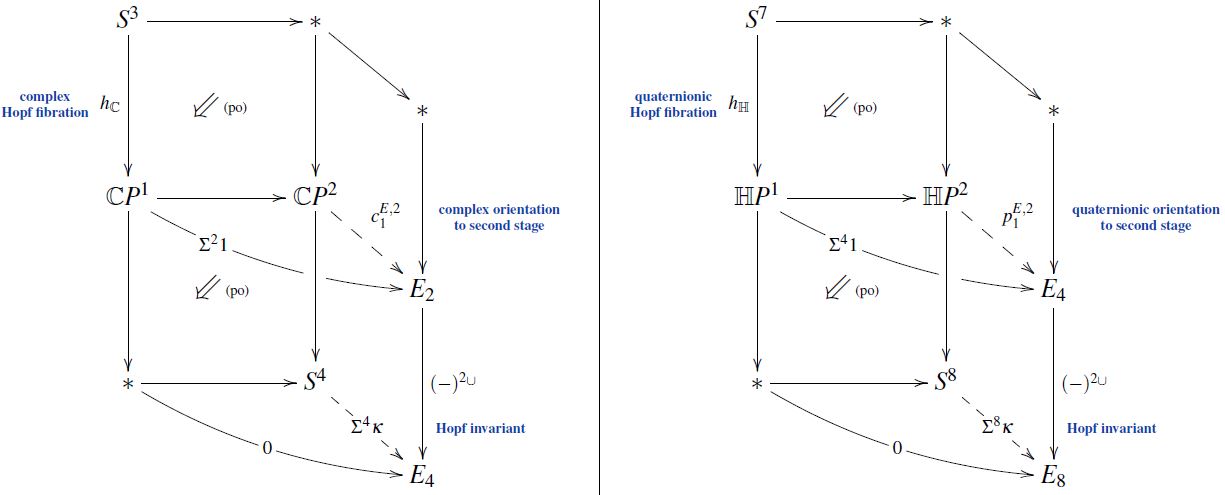
• for the complex Hopf fibration $f = h_{\mathbb{C}}$ the attaching space is complex projective space $\mathbb{C}P^2$ and the choice of homotopy $c$ is a choice of complex orientation to second stage;

• for the quaternionic Hopf fibration $f = h_{\mathbb{H}}$ the attaching space is quaternionic projective space $\mathbb{H}P^2$ and the choice of homotopy $c$ is a choice of quaternionic orientation to second stage.

Moreover, the de-composition of this pasting diagram exhibits the homotopy Whitehead integral/functional cup product-formula for the Hopf invariant:

from SS21

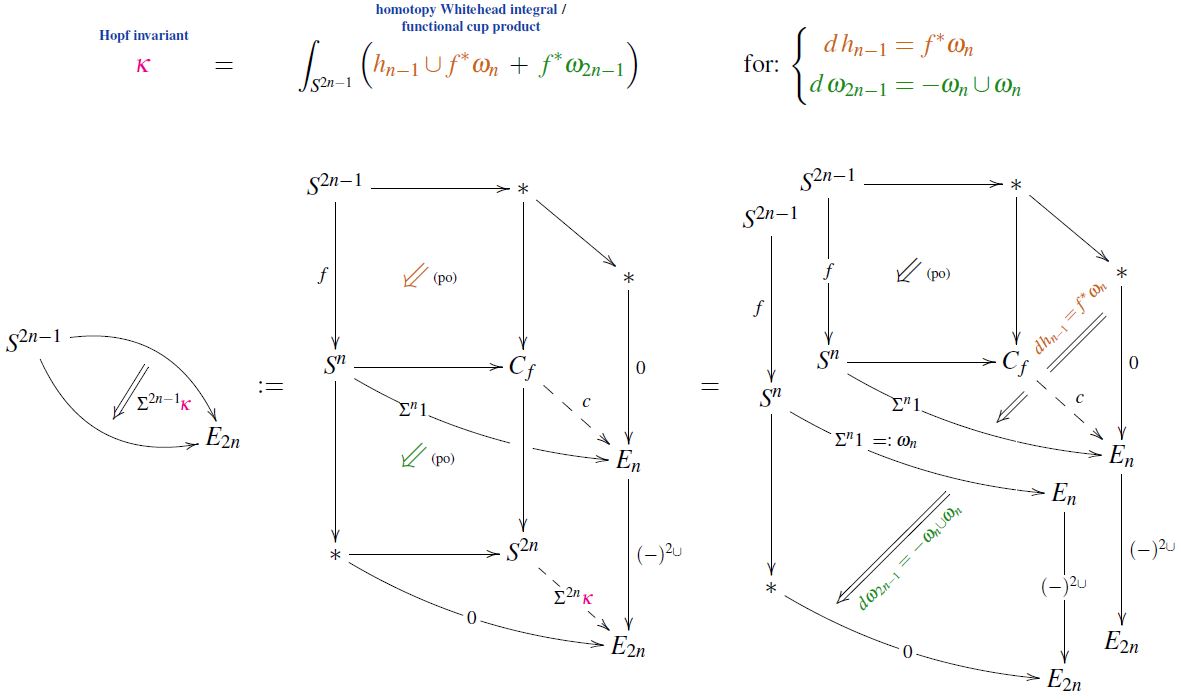
Properties

Generic values

For $n$ odd, the Hopf invariant necessarily vanishes. For $n$ even however, then there is a homomorphism

$$\pi_{2n-1}(S^n) \longrightarrow \mathbb{Z}$$

whose image contains at least the even integers.

Hopf invariant one

A famous open question in the 1950s was which maps $f$ (1) have Hopf invariant one, namely $[HI(f)] = 1$ (2).

The Hopf invariant one theorem (Adams60) states that the only maps of Hopf invariant one, $[HI(f)] = 1$, are the Hopf constructions on the four real normed division algebras:

• the real Hopf fibration;

• the complex Hopf fibration;

• the quaternionic Hopf fibration;

• the octonionic Hopf fibration.

Via Sullivan models

Proposition

By standard results in rational homotopy theory, every continuous function

$$S^{4k-1} \overset{f}{\longrightarrow} S^{2k}$$

corresponds to a unique dgc-algebra homomorphism

$$CE \big( \mathfrak{l}S^{4k-1} \big) \overset{ CE(\mathfrak{l}f) }{\longleftarrow} CE \big( \mathfrak{l}S^{2k} \big)$$

between Sullivan models of n-spheres.

The unique free coefficient of this homomorphism $CE(\mathfrak{l}f)$ is the Hopf invariant $HI(f)$ of $f$:

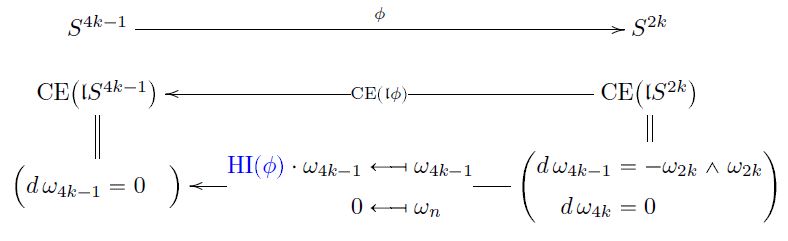
Whitehead integral formula

See at Whitehead integral formula and see the references below

Related concepts

• Hopf invariant one

• Whitehead integral formula

  • functional cup product

  • Hopf-Wess-Zumino term

• e-invariant

• Hopf degree theorem

• EHP spectral sequence

References

General

• Dale Husemöller, chapter 15 of: Fibre Bundles, Graduate Texts in Mathematics 20, Springer New York (1966) (doi:10.1007/978-1-4757-2261-1)

• Robert Mosher, Martin Tangora, p. 33 of Cohomology operations and applications in homotopy theory, Harper & Row 1986 (pdf)

• Michael Crabb, Andrew Ranicki, The Geometric Hopf Invariant and Surgery Theory, Springer Monographs in Mathematics, Springer (2017) $[$doi:10.1007/978-3-319-71306-9, slides pdf, pdf$]$

  (in relation to surgery theory)

• Klaus Wirthmüller, section 12 of: Vector bundles and K-theory, 2012 (pdf)

• Gereon Quick, The Hopf invariant one problem via K-theory, lecture notes in: Advanced algebraic topology, 2014 (pdf)

See also:

• Wikipedia, Hopf invariant

And see the references at Hopf invariant one for more, in particular for the formulation via topological K-theory.

Whitehead’s integral formula

Discussion via differential forms/real homotopy theory/rational homotopy theory (see also at functional cup product):

• J. H. C. Whitehead, An expression of Hopf’s invariant as an integral, Proc. Nat. Acad. Sci. USA 33 (1947), 117–123 (jstor:87688)

• Hassler Whitney, Section 31 in Geometric Integration Theory, 1957 (pup:3151)

• André Haefliger, p. 3 of Whitehead products and differential forms, In: P.A. Schweitzer (ed.), Differential Topology, Foliations and Gelfand-Fuks Cohomology, Lecture Notes in Mathematics, vol 652. Springer 1978 (doi:10.1007/BFb0063500)

• Raoul Bott, Loring Tu, Prop. 17.22 in Differential Forms in Algebraic Topology, Graduate Texts in Mathematics 82, Springer 1982 (doi:10.1007/BFb0063500)

• Lee Rudolph, Whitehead’s Integral Formula, Isolated Critical Points, and the Enhancement of the Milnor Number, Pure and Applied Mathematics Quarterly Volume 6, Number 2, 2010 (arXiv:0912.4974)

• Phillip Griffiths, John Morgan, Section 14.5 of: Rational Homotopy Theory and Differential Forms, Progress in Mathematics Volume 16, Birkhauser (1981, 2013) (doi:10.1007/978-1-4614-8468-4)

• Dev Sinha, Ben Walter, Lie coalgebras and rational homotopy theory II: Hopf invariants, Trans. Amer. Math. Soc. 365 (2013), 861-883 (arXiv:0809.5084, doi:10.1090/S0002-9947-2012-05654-6)

• Felix Wierstra, Hopf Invariants in Real and Rational Homotopy Theory (2017) [diva:146246, pdf]

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M5 WZ term level quantization, Comm. Math. Phys. 2020 (arXiv:1906.07417)