nLab e-invariant is Todd class of cobounding (U,fr)-manifold
Context
Algebraic topology
algebraic topology – application of higher algebra and higher category theory to the study of (stable) homotopy theory
Cobordism theory
cobordism theory = manifolds and cobordisms + stable homotopy theory/higher category theory
Concepts of cobordism theory
-
homotopy classes of maps to Thom space MO
-
complex cobordism cohomology theory
flavors of bordism homology theories/cobordism cohomology theories, their representing Thom spectra and cobordism rings:
bordism theoryM(B,f) (B-bordism):
relative bordism theories:
global equivariant bordism theory:
algebraic:
Contents
Idea
The e-invariant is, a priori, a homotopy invariant of morphisms in the stable homotopy category, hence in particular of the stable homotopy groups of spheres. Under the identification of the latter, via the Pontrjagin-Thom isomorphism, with the framed bordism ring, the e-invariant turns out to equal the Todd class of any cobounding (U,fr)-manifold (Conner-Floyd 66).
Preliminaries
Remark
In generalization to how the U-bordism ring is represented by homotopy classes of maps into the Thom spectrum MU, so the (U,fr)-bordism ring is represented by maps into the quotient spaces (for the canonical inclusion):
Remark
The bordism rings for MU, MUFr and MFr sit in a short exact sequence of the form
where is the evident inclusion, while is restriction to the boundary.
(By this Prop. at MUFr.)
In particular, this means that is surjective, hence that every -manifold is the boundary of a (U,fr)-manifold.
Statement
Proposition
(Todd class on cobounding (U,fr)-manifolds computes e-invariant)
Evaluation of the Todd class on (U,fr)-manifolds yields rational numbers which are integers on actual -manifolds. It follows with the short exact sequence (2) that assigning to -manifolds the Todd class of any of their cobounding -manifolds yields a well-defined element in Q/Z.
Under the Pontrjagin-Thom isomorphism between the framed bordism ring and the stable homotopy group of spheres , this assignment coincides with the Adams e-invariant in its Q/Z-incarnation:
(Conner-Floyd 66, Theorem 16.2)
Proof
The first step in the proof of (3) is the observation (Conner-Floyd 66, p. 100-101) that the representing map (1) for a (U,fr)-manifold cobounding a -manifold represented by a map is given by the following homotopy pasting diagram (see also at Hopf invariant – In generalized cohomology):
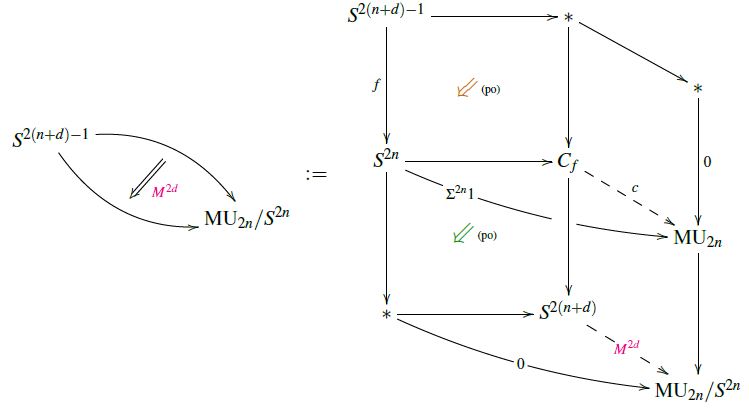
From this, Conner-Floyd conclude essentially by considering the following homotopy pasting diagram (the diagrammatic perspective here follows SS21, for more see at Adams e-invariant via unit cofiber theories):
Here for the identification of the Todd class in the bottom of the diagram we used that the rational Todd class is the Chern character of the Thom class.
That this Todd class equals the Q/Z-valued e-invariant follows now since the latter is the top-degree component of the Chern character of any complex topological K-theory-class lifting to (this Prop.).
Variants
An analogous but finer construction works for special unitary group-structure instead of unitary group-structure and in dimensions :
Since on -dimensional -manifolds the Todd class is divisible by 2 (Conner-Floyd 66, Prop. 16.4) we have (Conner-Floyd 66, p. 104) the following short exact sequence of MSUFr-bordism rings, in variation of (3):
This produces , the Adams e-invariant with respect to KO-theory instead of KU (Adams 66, p. 39), which, in degrees , is indeed half of the e-invariant for (by Adams 66, Prop. 7.14).
In fact, for we have:
Proposition
(Adams 66, Example 7.17 and p. 46)
In degree 3, the KO-theoretic e-invariant takes the value on the quaternionic Hopf fibration and hence reflects the full third stable homotopy group of spheres:
while sees only “half” of it (by Adams 66, Prop. 7.14).
Related statements
References
- Pierre Conner, Edwin Floyd, Theorem 16.2 in: The Relation of Cobordism to K-Theories, Lecture Notes in Mathematics 28 Springer 1966 (doi:10.1007/BFb0071091, MR216511)
An alternative formulation via index theory:
- Michael Atiyah, Vijay Patodi, Isadore Singer, Theorem 4.14 of: Spectral asymmetry and Riemannian geometry. II, Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78, Issue 3, 1975, pp. 405-432 (doi:10.1017/S0305004100051872)
Review in:
- Ulrich Bunke, Niko Naumann, Section 2 of: The f-invariant and index theory, Manuscripta Math. 132, 365–397 (2010) (arXiv:0808.0257, https://doi.org/10.1007/s00229-010-0351-7)
Last revised on January 15, 2021 at 18:17:45. See the history of this page for a list of all contributions to it.