nLab rho meson
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
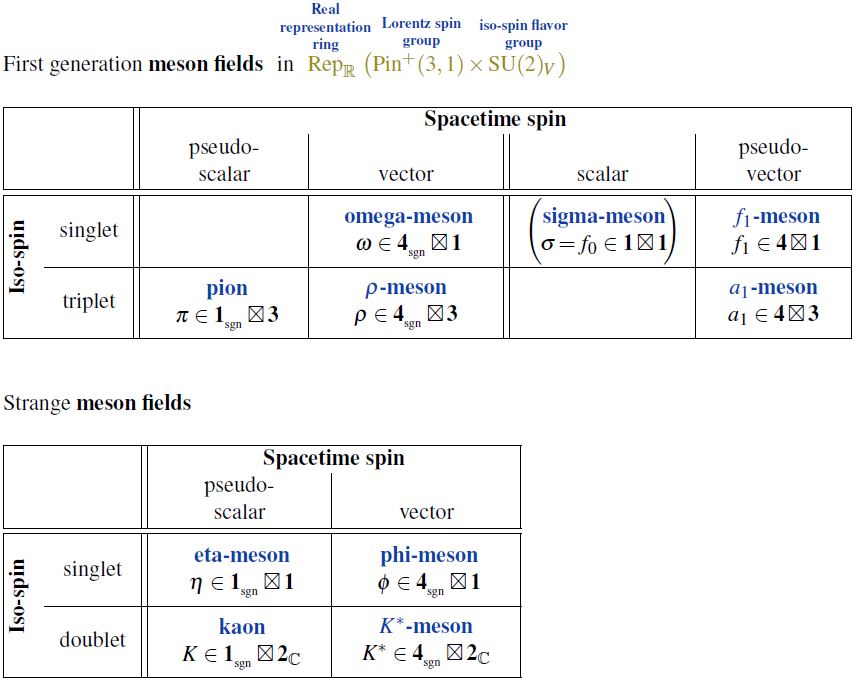
In nuclear physics, specifically in the chiral perturbation theory of quantum chromodynamics, the rho-meson is the isospin-triplet vector meson field in the first-generation of fermions, i.e. a bound state of an up quark and a down quark (a light meson), the chiral partner of the a1-meson;
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
Properties
Relation to Skyrmions
The skyrmion-model (see there) realizes baryons as solitons/instantons in a cloud of pions. If one adds to this also the ρ one gets also good Skyrmion models of light atomic nuclei (Naya=Sutcliffe 18)
Related concepts
References
General
See also
-
Wikipedia, Rho meson
-
Paul Singer, Radiative -Meson Decay, Phys. Rev. 130, 2441 (1963) (doi:10.1103/PhysRev.130.2441)
Via holographic light front QCD:
- Satvir Kaur, Chandan Mondal, Harleen Dahiya, Light-front holographic -meson distributions in the momentum space (arXiv:2009.04288)
Skyrme hadrodynamics with vector mesons (---model)
Inclusion of vector mesons (omega-meson and rho-meson/A1-meson) into the Skyrmion model of quantum hadrodynamics, in addition to the pion:
First, on the equivalence between hidden local symmetry- and massive Yang-Mills theory-description of Skyrmion quantum hadrodynamics:
- Atsushi Hosaka, H. Toki, Wolfram Weise, Skyrme Solitons With Vector Mesons: Equivalence of the Massive Yang-Mills and Hidden Local Symmetry Scheme, 1988, Z. Phys. A332 (1989) 97-102 (spire:24079)
See also
- Marcelo Ipinza, Patricio Salgado-Rebolledo, Meron-like topological solitons in massive Yang-Mills theory and the Skyrme model (arXiv:2005.04920)
Inclusion of the -meson
Original proposal for inclusion of the ω-meson in the Skyrme model:
- Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
Relating to nucleon-scattering:
- J. M. Eisenberg, A. Erell, R. R. Silbar, Nucleon-nucleon force in a skyrmion model stabilized by omega exchange, Phys. Rev. C 33, 1531 (1986) (doi:10.1103/PhysRevC.33.1531)
Combination of the omega-meson-stabilized Skyrme model with the bag model for nucleons:
- Atsushi Hosaka, Omega stabilized chiral bag model with a surface coupling, Nuclear Physics A Volume 546, Issue 3, 31 (1992) Pages 493-508 (doi:10.1016/0375-9474(92)90544-T)
Discussion of nucleon phenomenology for the -stabilized Skyrme model:
- Sven Bjarke Gudnason, James Martin Speight, Realistic classical binding energies in the -Skyrme model (arXiv:2004.12862)
Inclusion of the -meson
Original proposal for inclusion of the ρ-meson:
-
Y. Igarashi, M. Johmura, A. Kobayashi, H. Otsu, T. Sato, S. Sawada, Stabilization of Skyrmions via -Mesons, Nucl.Phys. B259 (1985) 721-729 (spire:213451, doi:10.1016/0550-3213(85)90010-0)
-
Gregory Adkins, Rho mesons in the Skyrme model, Phys. Rev. D 33, 193 (1986) (spire:16895, doi:10.1103/PhysRevD.33.193)
Discussion for phenomenology of light atomic nuclei:
-
Carlos Naya, Paul Sutcliffe, Skyrmions and clustering in light nuclei, Phys. Rev. Lett. 121, 232002 (2018) (arXiv:1811.02064)
-
Carlos Naya, Paul Sutcliffe, Skyrmions in models with pions and rho, JHEP 05 (2018) 174 (arXiv:1803.06098)
APS Synopsis: Revamping the Skyrmion Model, 2018
Inclusion of the - and -meson
The resulting -- model:
-
Ulf-G. Meissner, Ismail Zahed, Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
(includes also the A1-meson)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, Norbert Kaiser, Andreas Wirzba, Wolfram Weise, Skyrmions with and Mesons as Dynamical Gauge Bosons, Phys. Rev. Lett. 57, 1676 (1986) (doi:10.1103/PhysRevLett.57.1676)
-
Ulf-G. Meissner, Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
L. Zhang, Nimai C. Mukhopadhyay, Baryon physics from mesons: Leading order properties of the nucleon and in the chiral soliton model, Phys. Rev. D 50, 4668 (1994) (doi:10.1103/PhysRevD.50.4668, spire:384906)
-
Yong-Liang Ma, Ghil-Seok Yang, Yongseok Oh, Masayasu Harada, Skyrmions with vector mesons in the hidden local symmetry approach, Phys. Rev. D87:034023, 2013 (arXiv:1209.3554)
-
Ju-Hyun Jung, Ulugbek T. Yakhshiev, Hyun-Chul Kim, In-medium modified -- mesonic Lagrangian and properties of nuclear matter, Physics Letters B Volume 723, Issues 4–5, 25 June 2013, Pages 442-447 (arXiv:1212.4616, doi:10.1016/j.physletb.2013.05.042)
-
Ju-Hyun Jung, Ulugbek Yakhshiev, Hyun-Chul Kim, Peter Schweitzerm, In-medium modified energy-momentum tensor form factors of the nucleon within the framework of a -- soliton model, Phys. Rev. D 89, 114021 (2014) (arXiv:1402.0161)
-
Yongseok Oh, Skyrmions with vector mesons revisited (arXiv:1402.2821)
See also
- Ki-Hoon Hong, Ulugbek Yakhshiev, Hyun-Chul Kim, Modification of hyperon masses in nuclear matter, Phys. Rev. C 99, 035212 (2019) (arXiv:1806.06504)
Review:
-
Roland Kaiser, Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
-
Gottfried Holzwarth, Section 2.3 of: Electromagnetic Form Factors of the Nucleon in Chiral Soliton Models (arXiv:hep-ph/0511194), Chapter 2 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Yongseok Oh, Skyrmions with vector mesons: Single Skyrmion and baryonic matter, 2013 (pdf)
Combination of the omega-rho-Skyrme model with the bag model of quark confinement:
- H. Takashita, S. Yoro, H. Toki, Chiral bag plus skyrmion hybrid model with vector mesons for nucleon, Nuclear Physics A Volume 485, Issues 3–4, August 1988, Pages 589-605 (doi:10.1016/0375-9474(88)90555-6)
Inclusion of the -meson
Inclusion of the sigma-meson:
- Thomas D. Cohen, Explicit meson, topology, and the large- limit of the Skyrmion, Phys. Rev. D 37 (1988) (doi:10.1103/PhysRevD.37.3344)
For analysis of neutron star equation of state:
- David Alvarez-Castillo, Alexander Ayriyan, Gergely Gábor Barnaföldi, Hovik Grigorian, Péter Pósfay, Studying the parameters of the extended - model for neutron star matter (arXiv:2006.03676)
Last revised on September 10, 2020 at 18:40:32. See the history of this page for a list of all contributions to it.