nLab M-string

Idea

The brane intersection of an M2-brane with an M5-brane (i.e. a self-dual string in the M5’s worldvolume D=6 N=(2,0) SCFT is called an M-string if the other end of the M2-brane intersects another, parallel, M5-brane.

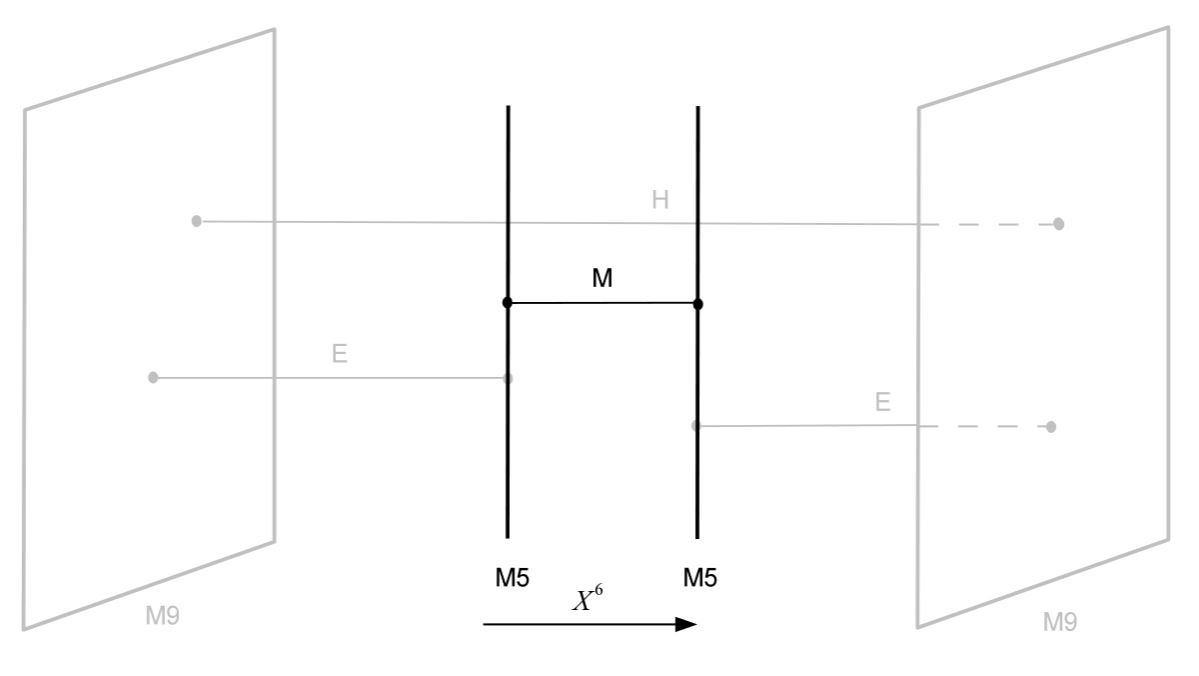
graphics grabbed from HLV 14

In contrast, if the other end of the M2 intersects an MO9-plane, then the former intersection is an E-string.

Properties

M-string elliptic genus

See at M-string elliptic genus.

Related concepts

brane intersections/bound states/wrapped branes/polarized branes

• D-branes and anti D-branes form bound states by tachyon condensation, thought to imply the classification of D-brane charge by K-theory

• intersecting D-branes/fuzzy funnels:

  • Dp-D(p+2)-brane bound state and Yang-Mills monopoles

    • D0-D2 brane bound state

    • D1-D3 brane bound state

    • D2-D4 brane bound state

    • D3-D5 brane bound state

    • D4-D6 brane bound state

    • D6-D8-brane bound state

  • Dp-D(p+4)-brane bound state and Yang-Mills instantons

    • D0-D4 brane bound state

    • D1-D5 brane bound state

    • D2-D6 brane bound state

    • D3-D7 brane bound state

    • D4-D8 brane bound state

    • D5-D9 brane bound state

      small instanton

• Dp-D(p+6) brane bound state

  • D0-D6 brane bound state

  • D1-D7 brane bound state

  • D2-D8 brane bound state

• NS5-D4-D2 bound states

• Hanany-Witten effect

S-duality$\,$bound states:

• (p,q)-string

• (p,q)5-branes

• string network

• 5-brane web

intersecting$\,$M-branes:

• M5-MO9 brane bound state

• M2-M5 brane bound state

  • M-string, E-string

• membrane triple junction

References

General

• Babak Haghighat, Amer Iqbal, Can Kozcaz, Guglielmo Lockhart, Cumrun Vafa, M-Strings, Commun. Math. Phys. 334, 779–842 (2015) (arXiv:1305.6322, doi:10.1007/s00220-014-2139-1)

• Babak Haghighat, Can Kozcaz, Guglielmo Lockhart, Cumrun Vafa, On orbifolds of M-Strings, Physical Review D 89.4 (2014): 046003 (arXiv:1310.1185)

Elliptic genera as super $p$-brane partition functions

The interpretation of elliptic genera (especially the Witten genus) as the partition function of a 2d superconformal field theory (or Landau-Ginzburg model) – and especially of the heterotic string (“H-string”) or type II superstring worldsheet theory has precursors in

• A. N. Schellekens, Nicholas P. Warner, Anomalies and modular invariance in string theory, Physics Letters B 177 (3-4), 317-323, 1986 (doi:10.1016/0370-2693(86)90760-4)

• A. N. Schellekens, Nicholas P. Warner, Anomalies, characters and strings, Nuclear Physics B Volume 287, 1987, Pages 317-361 (doi:10.1016/0550-3213(87)90108-8)

• Wolfgang Lerche, Bengt Nilsson, A. N. Schellekens, Nicholas P. Warner, Anomaly cancelling terms from the elliptic genus, Nuclear Physics B Volume 299, Issue 1, 28 March 1988, Pages 91-116 (doi:10.1016/0550-3213(88)90468-3)

and then strictly originates with:

• Edward Witten, Elliptic genera and quantum field theory, Comm. Math. Phys. Volume 109, Number 4 (1987), 525-536. (euclid:cmp/1104117076)

• Edward Witten, On the Landau-Ginzburg Description of $N=2$ Minimal Models, Int. J. Mod. Phys.A9:4783-4800,1994 (arXiv:hep-th/9304026)

• Toshiya Kawai, Yasuhiko Yamada, Sung-Kil Yang, Elliptic Genera and $N=2$ Superconformal Field Theory, Nucl. Phys. B414:191-212, 1994 (arXiv:hep-th/9306096, doi:10.1016/0550-3213(94)90428-6)

• Sujay K. Ashok, Jan Troost, A Twisted Non-compact Elliptic Genus, JHEP 1103:067, 2011 (arXiv:1101.1059)

• Matthew Ando, Eric Sharpe, Elliptic genera of Landau-Ginzburg models over nontrivial spaces, Adv. Theor. Math. Phys. 16 (2012) 1087-1144 (arXiv:0905.1285)

Review in:

• Miranda Cheng, (Mock) Modular Forms in String Theory and Moonshine, lecture notes 2016 (pdf)

• Katrin Wendland, Section 2.4 in: Snapshots of Conformal Field Theory, in: Mathematical Aspects of Quantum Field Theories Mathematical Physics Studies. Springer 2015 (arXiv:1404.3108, doi:10.1007/978-3-319-09949-1_4)

Formulations

Via super vertex operator algebra

Formulation via super vertex operator algebras:

• Hirotaka Tamanoi, Elliptic Genera and Vertex Operator Super-Algebras, Springer 1999 (doi:10.1007/BFb0092541)

• Chongying Dong, Kefeng Liu, Xiaonan Ma, Elliptic genus and vertex operator algebras, Algebr. Geom. Topol. 1 (2001) 743-762 (arXiv:math/0201135, doi:10.2140/agt.2001.1.743)

and for the topologically twisted 2d (2,0)-superconformal QFT (the heterotic string with enhanced supersymmetry) via sheaves of vertex operator algebras in

• Pokman Cheung, The Witten genus and vertex algebras (arXiv:0811.1418)

based on chiral differential operators:

• Vassily Gorbounov, Fyodor Malikov, Vadim Schechtman, Gerbes of chiral differential operators, Math. Res. Lett. 7(1), 55–66 (2000) (arXiv:math/9906117, arXiv:math/0003170, arXiv:math/0005201)

In relation to error-correcting codes:

• Kohki Kawabata, Shinichiro Yahagi, Elliptic genera from classical error-correcting codes $[$arXiv:2308.12592$]$

Via Dirac-Ramond operators on free loop space

Tentative interpretation as indices of Dirac-Ramond operators as would-be Dirac operators on smooth loop space:

• Edward Witten, The Index Of The Dirac Operator In Loop Space, in: Elliptic Curves and Modular Forms in Algebraic Topology, Lecture Notes in Mathematics 1326, Springer (1988) 161-181 [doi:10.1007/BFb0078045, spire]

  originating from:

  Edward Witten, p. 92-94 in: Global anomalies in string theory, in: W. Bardeen and A. White (eds.) Symposium on Anomalies, Geometry, Topology, World Scientific (1985) 61-99 [pdf, spire:214913]

• Orlando Alvarez, T. P. Killingback, Michelangelo Mangano, Paul Windey, The Dirac-Ramond operator in string theory and loop space index theorems, Nuclear Phys. B Proc. Suppl., 1A:189–215, 1987, in: Nonperturbative methods in field theory, 1987 (doi"10.1016/0920-5632(87)90110-1)

• Orlando Alvarez, T. P. Killingback, Michelangelo Mangano, Paul Windey, String theory and loop space index theorems, Comm. Math. Phys., 111(1):1–10, 1987 (euclid:cmp/1104159462)

• Gregory Landweber, Dirac operators on loop space, PhD thesis (Harvard 1999) (pdf)

• Orlando Alvarez, Paul Windey, Analytic index for a family of Dirac-Ramond operators, Proc. Natl. Acad. Sci. USA, 107(11):4845–4850, 2010 (arXiv:0904.4748)

Via conformal nets

Tentative formulation via conformal nets:

• Chris Douglas, André Henriques, Topological modular forms and conformal nets, in Hisham Sati, Urs Schreiber (eds.), Mathematical Foundations of Quantum Field and Perturbative String Theory, Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:1103.4187, doi:10.1090/pspum/083)

Conjectural interpretation in tmf-cohomology

The resulting suggestion that, roughly, deformation-classes (concordance classes) of 2d SCFTs with target space $X$ are the generalized cohomology of $X$ with coefficients in the spectrum of topological modular forms (tmf):

• Stephan Stolz, Peter Teichner, Supersymmetric field theories and generalized cohomology, in Hisham Sati, Urs Schreiber (eds.), Mathematical foundations of Quantum field theory and String theory, Proceedings of Symposia in Pure Mathematics, Volume 83, AMS 2011 (arXiv:1108.0189)

and the more explicit suggestion that, under this identification, the Chern-Dold character from tmf to modular forms, sends a 2d SCFT to its partition function/elliptic genus/supersymmetric index:

• Davide Gaiotto, Theo Johnson-Freyd, Section 5 of: Holomorphic SCFTs with small index, Canadian Journal of Mathematics (arXiv:1811.00589, doi:10.4153/S0008414X2100002X)

This perspective is also picked up in Gukov, Pei, Putrov & Vafa 18.

Discussion of the 2d SCFTs (namely supersymmetric SU(2)-WZW-models) conjecturally corresponding, under this conjectural identification, to the elements of $\mathbb{Z}/24$ $\simeq$ $tmf^{-3}(\ast) = \pi_3(tmf)$ $\simeq$ $\pi_3(\mathbb{S})$ (the third stable homotopy group of spheres):

• Davide Gaiotto, Theo Johnson-Freyd, Edward Witten, p. 17 of: A Note On Some Minimally Supersymmetric Models In Two Dimensions, (arXiv:1902.10249) in S. Novikov et al. Integrability, Quantization, and Geometry: II. Quantum Theories and Algebraic Geometry, Proc. Symposia Pure Math., 103(2), 2021 (ISBN: 978-1-4704-5592-7)

• Davide Gaiotto, Theo Johnson-Freyd, Mock modularity and a secondary elliptic genus (arXiv:1904.05788)

• Theo Johnson-Freyd, Topological Mathieu Moonshine (arXiv:2006.02922)

Discussion properly via (2,1)-dimensional Euclidean field theory:

• Daniel Berwick-Evans, How do field theories detect the torsion in topological modular forms? $[$arXiv:2303.09138$]$

• Daniel Berwick-Evans, How do field theories detect the torsion in topological modular forms?, talk at QFT and Cobordism, CQTS (Mar 2023) $[$web, video:YT$]$

See also:

• Ying-Hsuan Lin, Du Pei, Holomorphic CFTs and topological modular forms [arXiv:2112.10724]

• Jan Albert, Justin Kaidi, Ying-Hsuan Lin, Topological modularity of Supermoonshine $[$arXiv:2210.14923$]$

• Yuji Tachikawa, Mayuko Yamashita, Kazuya Yonekura, Remarks on mod-2 elliptic genus $[$arXiv:2302.07548$]$

• Yuji Tachikawa, Hao Y. Zhang, On a $\mathbb{Z}_3$-valued discrete topological term in 10d heterotic string theories [arXiv:2403.08861]

• Theo Johnson-Freyd, Mayuko Yamashita, On the 576-fold periodicity of the spectrum SQFT: The proof of the lower bound via the Anderson duality pairing [arXiv:2404.06333]

Occurrences in string theory

H-string elliptic genus

Further on the elliptic genus of the heterotic string being the Witten genus:

The interpretation of equivariant elliptic genera as partition functions of parametrized WZW models in heterotic string theory:

• Jacques Distler, Eric Sharpe, section 8.5 of Heterotic compactifications with principal bundles for general groups and general levels, Adv. Theor. Math. Phys. 14:335-398, 2010 (arXiv:hep-th/0701244)

• Matthew Ando, Equivariant elliptic cohomology and the Fibered WZW models of Distler and Sharpe, talk 2007 (lecture notes pdf)

Proposals on physics aspects of lifting the Witten genus to topological modular forms:

• Yuji Tachikawa, Topological modular forms and the absence of a heterotic global anomaly, Progress of Theoretical and Experimental Physics, 2022 4 (2022) 04A107 $[$arXiv:2103.12211, doi:10.1093/ptep/ptab060$]$

• Yuji Tachikawa, Mayuko Yamashita, Topological modular forms and the absence of all heterotic global anomalies, Comm. Math. Phys. 402 (2023) 1585-1620 $[$arXiv:2108.13542, doi:10.1007/s00220-023-04761-2$]$

• Yuji Tachikawa, Mayuko Yamashita, Anderson self-duality of topological modular forms, its differential-geometric manifestations, and vertex operator algebras $[$arXiv:2305.06196$]$

M5-brane elliptic genus

On the M5-brane elliptic genus:

A 2d SCFT argued to describe the KK-compactification of the M5-brane on a 4-manifold (specifically: a complex surface) originates with

• Juan Maldacena, Andrew Strominger, Edward Witten, Black Hole Entropy in M-Theory, JHEP 9712:002, 1997 (arXiv:hep-th/9711053)

Discussion of the resulting elliptic genus (2d SCFT partition function) originates with:

• Davide Gaiotto, Andrew Strominger, Xi Yin, The M5-Brane Elliptic Genus: Modularity and BPS States, JHEP 0708:070, 2007 (hep-th/0607010)

• Davide Gaiotto, Xi Yin, Examples of M5-Brane Elliptic Genera, JHEP 0711:004, 2007 (arXiv:hep-th/0702012)

Further discussion in:

• Murad Alim, Babak Haghighat, Michael Hecht, Albrecht Klemm, Marco Rauch, Thomas Wotschke, Wall-crossing holomorphic anomaly and mock modularity of multiple M5-branes, Comm. Math. Phys. 339 (2015) 773–814 $[$arXiv:1012.1608, doi:10.1007/s00220-015-2436-3$]$

• Sergei Gukov, Du Pei, Pavel Putrov, Cumrun Vafa, 4-manifolds and topological modular forms, J. High Energ. Phys. 2021 84 (2021) $[$arXiv:1811.07884, doi:10.1007/JHEP05(2021)084, spire:1704312$]$

M-string elliptic genus

On the elliptic genus of M-strings inside M5-branes:

• Stefan Hohenegger, Amer Iqbal, M-strings, Elliptic Genera and $\mathcal{N}=4$ String Amplitudes, Fortschritte der PhysikVolume 62, Issue 3 (arXiv:1310.1325)

• Stefan Hohenegger, Amer Iqbal, Soo-Jong Rey, M String, Monopole String and Modular Forms, Phys. Rev. D 92, 066005 (2015) (arXiv:1503.06983)

• M. Nouman Muteeb, Domain walls and M2-branes partition functions: M-theory and ABJM Theory (arXiv:2010.04233)

• Kimyeong Lee, Kaiwen Sun, Xin Wang, Twisted Elliptic Genera [arXiv:2212.07341]

E-string elliptic genus

On the elliptic genus of E-strings as wrapped M5-branes:

• J. A. Minahan, D. Nemeschansky, Cumrun Vafa, N. P. Warner, E-Strings and $N=4$ Topological Yang-Mills Theories, Nucl. Phys. B527 (1998) 581-623 (arXiv:hep-th/9802168)

• Wenhe Cai, Min-xin Huang, Kaiwen Sun, On the Elliptic Genus of Three E-strings and Heterotic Strings, J. High Energ. Phys. 2015, 79 (2015). (arXiv:1411.2801, doi:10.1007/JHEP01(2015)079)

On the elliptic genus of E-strings as M2-branes ending on M5-branes:

• Joonho Kim, Seok Kim, Kimyeong Lee, Jaemo Park, Cumrun Vafa, Elliptic Genus of E-strings, JHEP 1709 (2017) 098 (arXiv:1411.2324)