nLab black brane

Idea

The theory of gravity in $3+1$ dimensions famously has black hole solutions, being the limiting configuration of a point mass gravitational source. In higher dimensional gravity, and in particular in higher dimensional supergravity, there are analogous solutions, which however are limiting configurations of a gravitational source that is supported on a line, or a surface, or a higher dimensional space. For a surface one might speak of black membrane solutions hence generally of black brane solutions.

Particularly the BPS states among the black branes in supergravity, i.e. those solutions that carry Killing spinors, include configurations that look like the strong-coupling version of the Green-Schwarz super p-branes.

1/2 BPS black branes in supergravity: D-branes, F1-brane, NS5-brane, M2-brane, M5-brane

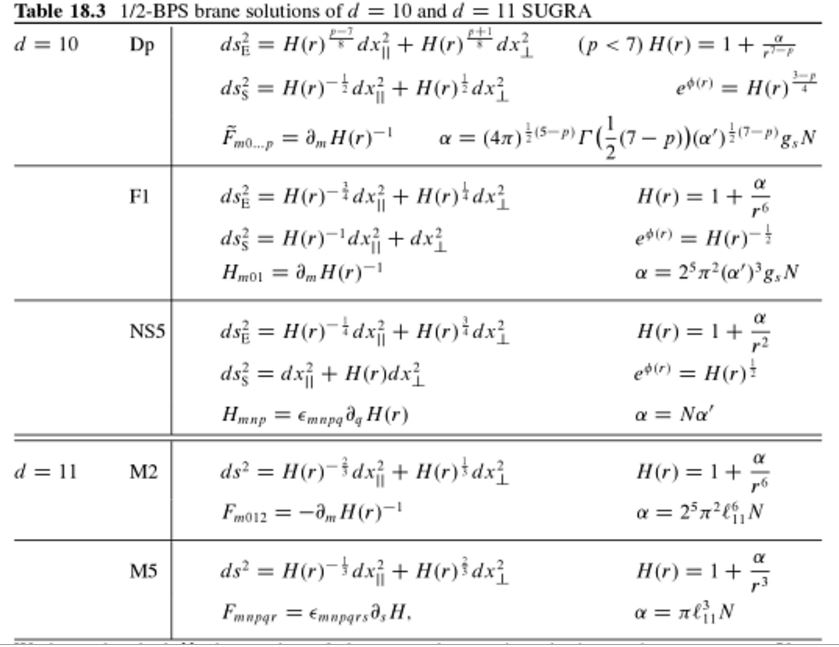
(table from Blumenhagen, Lüst & Theisen 2013, Chapter 18.5)

The near-horizon geometry of these black branes is generically that of anti de Sitter spacetime times a sphere. To the extent that the worldvolume theory of the branes is a superconformal QFT, this is the origin of the AdS-CFT correspondence.

Properties

Weak coupling correspondence

The types of black branes that can occur in theories of supergravity that are obtained from the maximal 11-dimensional supergravity match precisely the types of D-branes and NS-branes that appear in the corresponding perturbative superstring theories.

The idea is that both these brane-phenomena are aspects of one single entity:

• At low string coupling the D-brane/NS-brane description is accurate. Low string coupling implies that the coupling of gravity is weak, hence that the back-reaction of the branes on the background geometry is negligible.

• At large string coupling but low energy, the effective supergravity description becomes accurate. Here the branes do back-react on the gravitational background and hence create the black brane spacetime geometry.

This duality of the brane picture is at the heart of the AdS/CFT correspondence. See there for more details.

Examples

• black hole, black hole in string theory

• black string

• black membrane?

• black fivebrane

• string triple junction

• membrane triple junction

Related concepts

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

brane	in supergravity	charged under gauge field	has worldvolume theory
black brane	supergravity	higher gauge field	SCFT
D-brane	type II	RR-field	super Yang-Mills theory
$(D = 2n)$	type IIA	$\,$	$\,$
D(-2)-brane	$\,$	$\,$
D0-brane	$\,$	$\,$	BFSS matrix model
D2-brane	$\,$	$\,$	$\,$
D4-brane	$\,$	$\,$	D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane	$\,$	$\,$	D=7 super Yang-Mills theory
D8-brane	$\,$	$\,$
$(D = 2n+1)$	type IIB	$\,$	$\,$
D(-1)-brane	$\,$	$\,$	$\,$
D1-brane	$\,$	$\,$	2d CFT with BH entropy
D3-brane	$\,$	$\,$	N=4 D=4 super Yang-Mills theory
D5-brane	$\,$	$\,$	$\,$
D7-brane	$\,$	$\,$	$\,$
D9-brane	$\,$	$\,$	$\,$
(p,q)-string	$\,$	$\,$	$\,$
(D25-brane)	(bosonic string theory)
NS-brane	type I, II, heterotic	circle n-connection	$\,$
string	$\,$	B2-field	2d SCFT
NS5-brane	$\,$	B6-field	little string theory
D-brane for topological string			$\,$
A-brane			$\,$
B-brane			$\,$
M-brane	11D SuGra/M-theory	circle n-connection	$\,$
M2-brane	$\,$	C3-field	ABJM theory, BLG model
M5-brane	$\,$	C6-field	6d (2,0)-superconformal QFT
M9-brane/O9-plane			heterotic string theory
M-wave
topological M2-brane	topological M-theory	C3-field on G₂-manifold
topological M5-brane	$\,$	C6-field on G₂-manifold
S-brane
SM2-brane, membrane instanton
M5-brane instanton
D3-brane instanton
solitons on M5-brane	6d (2,0)-superconformal QFT
self-dual string		self-dual B-field
3-brane in 6d

References

By “black branes” one mostly refers to – generally higher-dimensional – singular solutions of theories of supergravity, referenced below at

• Black branes in supergravity

But closely related discussion has historically been had on the possibility of identifying electrons and other fundamental particles with Kerr-Newman black holes (“black 0-branes”):

Matching KN black holes to elementary particles

On the similarity between Kerr-Newman black holes (charged and spinning “black 0-branes”) and elementary particles (sigma-model 0-branes) like electrons.

Historical precursor discussion on the possibility of geometrodynamics for fundamental particles:

• Albert Einstein, Leopold Infeld, B. Hoffmann, The gravitational equations and the problem of motion, Annals of Mathematics 39 1 (1938) [doi:10.2307/1968714, jstor:1968714]

Seminal observation that the gyromagnetic ratio of the Kerr-Newman black hole is 2, just as the for electron (cf. at anomalous magnetic moment):

• Brandon Carter, p. 1562 of: Global Structure of the Kerr Family of Gravitational Fields, Phys. Rev. 174 (1968) 1559 [doi:10.1103/PhysRev.174.1559]

• Werner Israel, Source of the Kerr Metric, Phys. Rev. D 2 641 (1970) [doi:10.1103/PhysRevD.2.641]

Further discussion:

• Carlos A. López, Extended model of the electron in general relativity, Phys. Rev. D 30 313 (1984) [doi:10.1103/PhysRevD.30.313]

• H. I. Arcos, J. G. Pereira: Kerr–Newman Solution as a Dirac Particle, General Relativity and Gravitation 36 (2004) 2441–2464 [doi:10.1023/B:GERG.0000046832.71368.a5, arXiv:hep-th/0210103]

• Alexander Burinskii, The Dirac-Kerr-Newman electron, Gravit. Cosmol. 14 (2008) 109–122 [doi:10.1134/S0202289308020011, arXiv:hep-th/0507109]

• Alexander Burinskii, Kerr–Newman electron as spinning soliton, International Journal of Modern Physics A 29 26, 1450133 (2014) [doi:10.1142/S0217751X14501334, arXiv:1410.2888]

See also:

• Wikipedia, Black hole electron

Black branes in supergravity

Original articles on black branes in supergravity (and thereby in string/M-theory):

• Michael Duff, Ramzi R. Khuri, Jian Xin Lu, String and Fivebrane Solitons: Singular or Non-singular?, Nucl.Phys. B 377 (1992) 281-294 [arXiv:hep-th/9112023, doi:10.1016/0550-3213(92)90025-7]

• Michael Duff, Jian Xin Lu, Black and super $p$-branes in diverse dimensions, Nucl. Phys. B 416 (1994) 301-334 [arXiv:hep-th/9306052, doi:10.1016/0550-3213(94)90586-X]

• Mike Duff, Ramzi R. Khuri, Jian Xin Lu, String Solitons, Phys. Rept. 259 (1995) 213-326 [arXiv:hep-th/9412184, doi:10.1016/0370-1573(95)00002-X]

  (solitonic branes)

• Michael Duff, H. Lu, Christopher Pope, The Black Branes of M-theory, Phys. Lett. B 382 (1996) [arXiv:hep-th/9604052]

The M5-brane was maybe first found as a black brane of 11-dimensional supergravity (the black fivebrane) in

• Rahmi Gueven, Black $p$-brane solutions of $D = 11$ supergravity theory, Phys. Lett. B276 (1992) 49 and in Mike Duff (ed.)The World in Eleven Dimensions_ 135-141 (spire:338203)

The observation that black $p$-branes metric for odd $p$ are completely non-singular is due to

• Gary Gibbons, Gary Horowitz, Paul Townsend, p. 15 of Higher-dimensional resolution of dilatonic black hole singularities, Class. Quant. Grav.12:297-318,1995 (arXiv:hep-th/9410073)

The suggestion that extremal/BPS state black branes are the strong coupling incarnation of fundamental branes originates in

• Chris Hull, Paul Townsend, Unity of Superstring Dualities, Nucl. Phys. B 438 (1995) 109-137 [arXiv:hep-th/9410167]

• Edward Witten, p. 6 (bottom) of: String Theory Dynamics In Various Dimensions, Nucl. Phys. B 443 (1995) 85-126 [arXiv:hep-th/9503124]

Review:

• Mike Duff, chapter 5 of: The World in Eleven Dimensions: Supergravity, Supermembranes and M-theory, IoP (1999) [ISBN:9780750306720]

• Kellogg Stelle, around section 3.3 of: BPS Branes in Supergravity, in: Quantum Field Theory: Perspective and Prospective, NATO Science Series 530 (1999) 257-351 [arXiv:hep-th/9803116, doi:10.1007/978-94-011-4542-8_12]

• Ofer Aharony, S. S. Gubser, Juan Maldacena, H. Ooguri, Y. Oz, section 1.3 of Large N Field Theories, String Theory and Gravity [arXiv:hep-th/9905111]

• Thomas Mohaupt, Black holes in supergravity and string theory, Class. Quantum Grav. 17 (2000) 3429–3482 (pdf)

• Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, Brane solutions in supergravity, chapter 18.5 in: Basic Concepts of String Theory, Springer (2013) [doi:10.1007/978-3-642-29497-6]

and in the context of multiple M2-branes in the BLG model:

• Jonathan Bagger, Neil Lambert, Sunil Mukhi, Constantinos Papageorgakis, section 1.6 of Multiple Membranes in M-theory (arXiv:1203.3546)

Further developments include

• Gerard Clement, Dmitri Gal’tsov, Cedric Leygnac, Black branes on the linear dilaton background, Phys. Rev. D71 (2005) 084014 (arXiv:hep-th/0412321)

• D. Gal’tsov, S. Klevtsov, D. Orlov, G. Clement, More on general $p$-brane solutions, Int.J.Mod.Phys.A21:3575-3604, 2006 (arXiv:hep-th/0508070)

• Michael Duff, Near-horizon brane scan revived, Nucl. Phys. B810:193-209, 2009 (arXiv:0804.3675)

• Jay Armas, Joan Camps, Troels Harmark, Niels A. Obers, The Young Modulus of Black Strings and the Fine Structure of Blackfolds (arXiv:1110.4835)

Blackfold approach

• Roberto Emparan, Troels Harmark, Vasilis Niarchos, Niels A. Obers, Essentials of Blackfold Dynamics, JHEP 1003 063 (2010) [arXiv:0910.1601, doi:10.1007/JHEP03(2010)063]

• Roberto Emparan, Troels Harmark, Vasilis Niarchos, Niels A. Obers, Blackfolds in Supergravity and String Theory, JHEP 1108 (2011) 154 [arXiv:1106.4428doi:10.1007/JHEP08(2011)154]

Microscopic AdS/CFT via $p$-brane sigma-models

Over a decade before the modern formulation of the AdS-CFT correspondence, a candicate “microscopic” explanation was observed:

Immersing the worldvolume of a sigma-model super $p$-brane (hence a “light” brane without backreaction) along the near horizon geometry (an AdS supergravity solution) of its own black brane incarnation (hence the “heavy” incarnation of the same brane, causing backreaction), its worldvolume fluctuations (after super-diffeomorphism gauge fixing) are described by the corresponding superconformal field theory (exhibited by superconformal multiplets such as “supersingletons”) [graphics from GSS24].

The original observation for the M2-brane:

• Eric Bergshoeff, Michael Duff, Christopher Pope, Ergin Sezgin: Supersymmetric Supermembrane Vacua and Singletons, Phys. Lett. B 199 (1987) 69-74 [doi:10.1016/0370-2693(87)91465-1, InSpire:250244]

• Miles P. Blencowe, Mike Duff, Supersingletons, Physics letters B, 203 3 (1988) 229-236 [doi:10.1016/0370-2693(88)90544-8, cds:184143]

• Gianguido Dall'Agata, Davide Fabbri, Christophe Fraser, Pietro Fré, Piet Termonia, Mario Trigiante, The $Osp(8|4)$ singleton action from the supermembrane, Nucl. Phys. B 542 (1999) 157-194 [doi:10.1016/S0550-3213(98)00765-2, arXiv:hep-th/9807115]

with popular exposition in:

• Mike Duff, Christine Sutton: The Membrane at the End of the Universe, New Scientist 118 (1988) 67-71 [inspire:268230, ISSN:0028-6664]

Further discussion including also M5-branes and D-branes:

• Piet Claus, Renata Kallosh, Antoine Van Proeyen, M 5-brane and superconformal $(0,2)$ tensor multiplet in 6 dimensions, Nucl. Phys. B 518 (1998) 117-150 [doi:10.1016/S0550-3213(98)00137-0, arXiv:hep-th/9711161]

• Piet Claus, Renata Kallosh, J. Kumar, Paul K. Townsend, Antoine Van Proeyen, Conformal Theory of M2, D3, M5 and “D1+D5” Branes, JHEP 9806 (1998) 004 [doi:10.1088/1126-6708/1998/06/004, arXiv:hep-th/9801206]

• Paolo Pasti, Dmitri Sorokin, Mario Tonin, Branes in Super-AdS Backgrounds and Superconformal Theories, Proceedings, International Workshop on Supersymmetries and Quantum Symmetries (SQS’99), Moscow (July 27-31, 1999) [arXiv:hep-th/9912076, inspire:511348]

• C. Grojean, J. Mourad, Super fivebranes near the boundary of $AdS_7 \times S^4$, Nuclear Physics B 567 1–2 (2000) 133-150 [doi:10.1016/S0550-3213(99)00335-1, arXiv:hep-th/9903164]

• Alexei Nurmagambetov, I. Y. Park On the M5 and the $\mathrm{AdS}_7/CFT_6$ correspondence, Physics Letters B

  524 1–2 (2002) 185-191 [doi:10.1016/S0370-2693(01)01375-2, arXiv:hep-th/0110192]

Review:

• Mike Duff, Anti-de Sitter space, branes, singletons, superconformal field theories and all that, Int. J. Mod. Phys. A 14 (1999) 815-844 [doi:10.1142/S0217751X99000403, arXiv:hep-th/9808100]

• Mike Duff, TASI Lectures on Branes, Black Holes and Anti-de Sitter Space, lectures at 9th CRM Summer School: Theoretical Physics at the End of the 20th Century at TASI 99 (1999) [arXiv:hep-th/9912164, inspire:511822]

The resulting super-conformal brane scan:

• Michael Duff, Near-horizon brane-scan revived, Nucl. Phys. B 810 (2009) 193-209 [doi:10.1016/j.nuclphysb.2008.11.001, arXiv:0804.3675]

• Michael Duff, The conformal brane-scan: an update, J. High Energ. Phys. 2022 54 (2022) [doi:10.1007/JHEP06(2022)054, arXiv:2112.13784]

Related:

• Hironori Mori, Satoshi Yamaguchi, §3 in: M5-branes and Wilson Surfaces in AdS7/CFT6 Correspondence, Phys. Rev. D 90 (2014) 026005 [doi:10.1103/PhysRevD.90.026005, arXiv:1404.0930]

Analogous discussion for embeddings with less supersymmetry, corresponding to defects

• Nadav Drukker, Simone Giombi, Arkady A. Tseytlin, Xinan Zhou, Defect CFT in the 6d $(2,0)$ theory from M2 brane dynamics in $AdS_7 \times S^4$, J. High Energ. Phys. 2020 101 (2020) [doi:10.1007/JHEP07(2020)101, arXiv:2004.04562]

• Varun Gupta, Holographic M5 branes in $\mathrm{AdS}_7 \times S^4$, J. High Energ. Phys. 2021 32 (2021) [doi:10.1007/JHEP12(2021)032, arXiv:2109.08551]

• Varun Gupta, More Holographic M5 branes in $\mathrm{AdS}_7 \times S^4$, Phys. Lett. B 853 (2024) 138650 [doi:10.1016/j.physletb.2024.138650, arXiv:2301.02528]