nLab 11d supergravity Lie 3-algebra
Context
-Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Contents
Definition
The supergravity Lie 3-algebra or M2-brane extension is a super L-∞ algebra that is a shifted extension
of the super Poincare Lie algebra in 10+1 dimensions induced by the exceptional degree 4-super Lie algebra cocycle
This is the same mechanism by which the String Lie 2-algebra is a shifted central extension of .
Properties
The Chevalley-Eilenberg algebra
Proposition
The Chevalley-Eilenberg algebra is generated on
-
elements and of degree
-
a single element of degree
-
and elements of degree
with the differential defined by
(fill in details)
Hidden super Lie 1-algebra
At the end of (D’Auria-Fre 82) the authors ask for a super Lie 1-algebra , equipped with a degree-3 element in its Chevalley-Eilenberg algebra, and equipped with a homomorphism such that the pullback of the 4-cocycle along is trivialized by :
In the homotopy theory of L-infinity algebras? this means that
Compare this to the characterization of as the homotopy fiber of , hence as the universal solution to this situation
In any case, in (D’Auria-Fre 82) possible choices for are found.
Curiously, the bosonic body of is such that when adapted to a compactification to 4d, then it is the exceptional tangent bundle on which the U-duality group E7 has a canonical action.
In (BAIPV 04) these solutions are shown to extend to a 1-parameter family of solutions. Further comments are in (Andrianopoli-D’Auria-Ravera 16).
Relation to M5-brane action functional
The supergravity Lie 3-algebra carries a 7-cocycle (the one that induces the supergravity Lie 6-algebra-extension of it). The corresponding WZW term is that of the M5-brane in its Green-Schwarz action functional-like formulation.
The brane scan.
The Green-Schwarz type super -brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | M2 | M5 | ||||||||
| 10 | D0 | F1, D1 | D2 | D3 | D4 | NS5, D5 | D6 | D7 | D8 | D9 |
| 9 | * | |||||||||
| 8 | * | |||||||||
| 7 | M2 | |||||||||
| 6 | F1, S1 | S3 | ||||||||
| 5 | * | |||||||||
| 4 | * | * | ||||||||
| 3 | * |
(The first columns follow the exceptional spinors table.)
The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | on sIso(10,1) | on m2brane | ||||||||
| 10 | on sIso(9,1) | on StringIIA | on StringIIB | on StringIIA | on sIso(9,1) | on StringIIA | on StringIIB | in StringIIA | on StringIIB | |
| 9 | on sIso(8,1) | |||||||||
| 8 | on sIso(7,1) | |||||||||
| 7 | on sIso(6,1) | |||||||||
| 6 | on sIso(5,1) | on sIso(5,1) | ||||||||
| 5 | on sIso(4,1) | |||||||||
| 4 | on sIso(3,1) | on sIso(3,1) | ||||||||
| 3 | on sIso(2,1) |
The Brane molecule
Furthermore, there exists a more general classification of possible supermembranes in spacetime with spatial dimensions and time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.
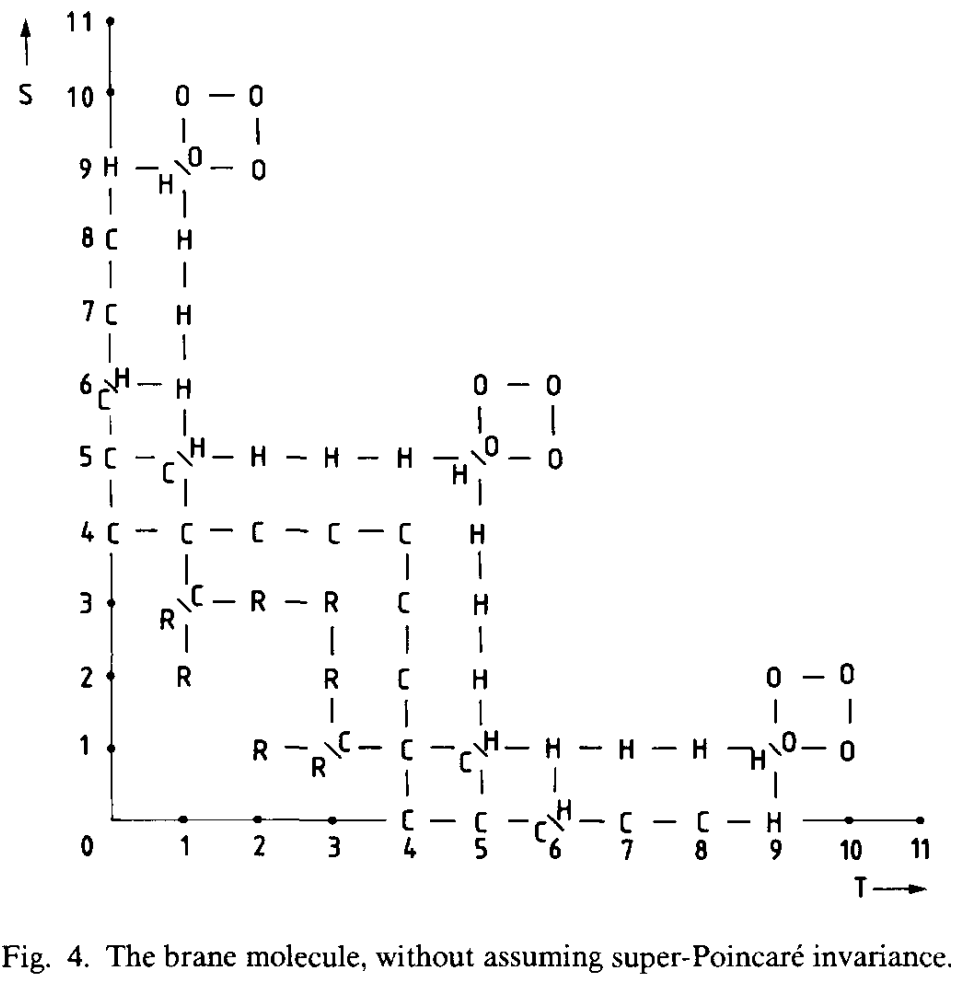
Compare:
-
Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)
Relation to the 11-dimensional polyvector super Poincaré-algebra
Via derivations
Proposition
Let be the automorphism ∞-Lie algebra of . This is a dg-Lie algebra. Write for the ordinary Lie algebra in degree 0.
This is isomorphic to the polyvector-extension of the super Poincaré Lie algebra (see there) in – the “M-theory super Lie algebra” – with “2-brane central charge”: the Lie algebra spanned by generators and graded Lie brackets those of the super Poincaré Lie algebra as well as
etc.
This observation appears implicitly in (Castellani 05, section 3.1), see (FSS 13).
Proof
With the presentation of the Chevalley-Eilenberg algebra as in prop. above, the generators are identified with derivations on as
and
and
and
etc. With this it is straightforward to compute the commutators. Notably the last term in
arises from the contraction of the 4-cocycle with .
Via the Heisenberg Lie 3-algebras
(…)
Applications
The field configurations of 11-dimensional supergravity may be identified with ∞-Lie algebra-valued forms with values in . See D'Auria-Fre formulation of supergravity.
Related concepts
supergravity Lie 6-algebra supergravity Lie 3-algebra super Poincaré Lie algebra
References
The Chevalley-Eilenberg algebra of first appears in (3.15) of
- Riccardo D'Auria, Pietro Fré, Geometric Supergravity in D=11 and its hidden supergroup, Nuclear Physics B201 (1982)
and later in the textbook
- Leonardo Castellani, Riccardo D'Auria, Pietro Fré, Supergravity and Superstrings - A Geometric Perspective
The manifest interpretation of this as a Lie 3-algebra and the supergravity field content as ∞-Lie algebra valued forms with values in this is mentioned in
-
Hisham Sati, Urs Schreiber, Jim Stasheff, L-∞ algebra connections
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields
A systematic study of the super-Lie algebra cohomology involved is in
-
John Baez, John Huerta, Division algebras and supersymmetry I (arXiv:0909.0551)
-
John Baez, John Huerta, Division algebras and supersymmetry II (arXiv:1003.34360)
See also division algebra and supersymmetry.
Further discussion of its “hidden” super Lie algebra includes
-
Igor Bandos, José de Azcárraga, José M. Izquierdo, Moises Picon, Oscar Varela, On the underlying gauge group structure of supergravity, Phys. Lett. B 596 (2004) 145-155 [arXiv;hep-th/0406020]
-
Igor Bandos, Jose de Azcarraga, Moises Picon, Oscar Varela, On the formulation of supergravity and the composite nature of its three-from field, Annals Phys. 317 (2005) 238-279 [arXiv:hep-th/0409100]
-
Laura Andrianopoli, Riccardo D'Auria, Lucrezia Ravera, Hidden Gauge Structure of Supersymmetric Free Differential Algebras [arXiv:1606.07328]
Further review:
- Lucrezia Ravera, On the hidden symmetries of supergravity [arXiv:2112.00445]
The computation of the automorphism Lie algebra of is in
- Leonardo Castellani, Lie derivatives along antisymmetric tensors and the M-theory superalgebra, J. Phys. Math. 3 (2011) 1-7 [arXiv:hep-th/0508213]
A similar argument with more explicit use of the Lie 3-algebra as underlying the Green-Schwarz-like action functional for the M5-brane is in
- Dmitri Sorokin, Paul Townsend, M-theory superalgebra from the M-5-brane, Phys. Lett. B 412 (1997) 265-273 [arXiv:hep-th/9708003]
Last revised on February 25, 2024 at 16:21:13. See the history of this page for a list of all contributions to it.