nLab NS5-brane
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
- Idea
- Properties
- As a black brane
- Relation to little string theory
- D-branes ending on NS5-branes
- Open D-brane theories on the NS5
- D4-branes ending on NS5-branes
- D6-branes ending on NS5-branes
- D6 branes intersecting D8-branes over NS5-branes
- NS5 half-branes
- Webs
- NS5/D4/D2 bound states
- Relation to Khovanov homology
- Related concepts
- References
Idea
In the context of string theory the NS5-brane is a certain extended physical objects – a brane – that appears in/is predicted by the theory.
There are different incarnations of this object:
For instance the effective background QFT of the type II string – type II supergravity – admits solutions to its generalized Einstein equations which describe higher dimensional analogs of charged black holes in ordinary gravity. Among them is a 5+1-dimensional “black brane” which is magnetically charged under the Kalb-Ramond field. Since the KR field and the field of gravity constituting this solution of type II supergravity have as quanta the worldsheet excitations of the spinning string sigma-model that sit in what is called the Neveu-Schwarz sector? one calls this the NS5-brane.
This is to distinguish it from the D5-brane which is instead charged under the RR-field whose quanta come from the Ramond-Ramond sector? of the superstring.
There are other incarnations of the NS 5-brane:
by the general logic of higher electromagnetism the (1+1)-dimensional string has under electric-magnetic duality a magnetic dual . By dimension counting this is a 5-brane. If we think of the string this way as the structure that supports the sigma-model that defines perturbative string theory, we also call it the F1-brane (the fundamental 1-brane). In this sense the the corresponding magnetic dual is the F5-brane – the fundamental fivebrane.
One can understand the NS5-“black brane” solution to type II supergravity as being the solitonic incarnation of the fundamental 5-brane in much the same way as an ordinary black hole in ordinary gravity is a solitonic incarnation of the fundamental particle: as the particle, the black hole it is characterized just by mass, charge and angular momentum.
Similarly, the “black” NS5-brane is characterizes by mass, B-field charge and angular momentum.
Properties
As a black brane
1/2 BPS black branes in supergravity: D-branes, F1-brane, NS5-brane, M2-brane, M5-brane
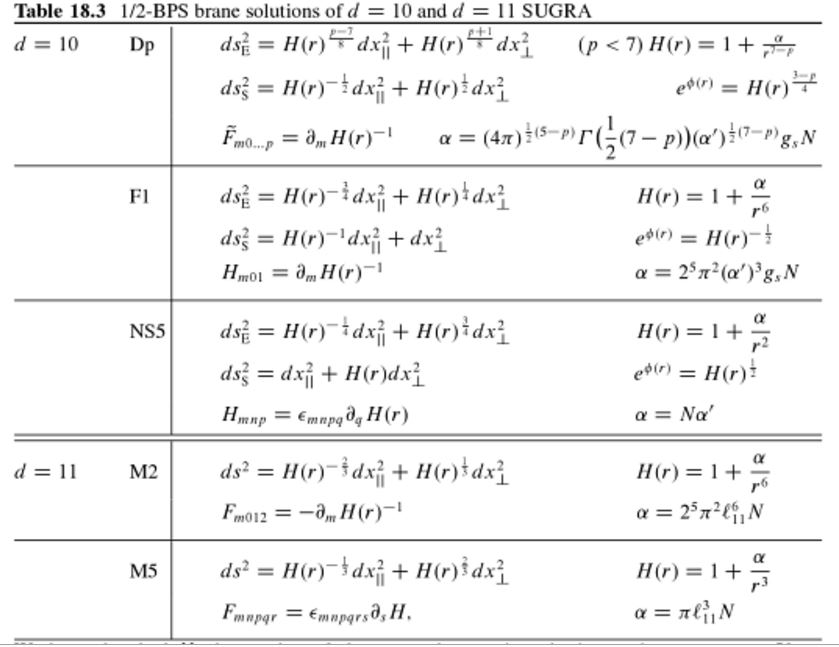
(table from Blumenhagen, Lüst & Theisen 2013, Chapter 18.5)
Relation to little string theory
By the brane scan, on the worldvolume of an NS5-brane propagates a superstring. This is called the little string, see there for more.
D-branes ending on NS5-branes
The black D-branes may end on black NS5-branes (Callan-Harvey-Strominger 91, sections IV.C and V.B, Tseytlin 96, Argurio-Englert-Houart 97, Brodie-Hanany 97, EGKRS 00).
One way to see this is to analyze the twisted Bianchi identity for the RR-field flux densities sourced by D-branes, in the presence of the B-field-flux density which is sourced by the NS5-brane – see at Hanany-Witten effect for this analysis.
Another way to see this is to assume that S-duality and T-duality work as expected, since then the B/NS5 intersections appear as “duals” of the intersections of the fundamental string with D-branes which exist by definition of D-branes:
This leads to what is called geometric engineering of quantum field theory on the worldvolume of these branes (following Hanany-Witten 1997, review includes Fazzi 17).
Open D-brane theories on the NS5
Combining the above two items, the corresponding worldvolume theories of the NS5-branes (see also at little string theory) in the presence of light D-branes ending on/inside them are also referred to as “open D-brane theories” or “OD theories” (Gopakumar-Minwalla-Seiberg-Strominger 00, section 6, Harmark 00, section 4.2, Lu 06, section 6)
D4-branes ending on NS5-branes
See Witten 1997.
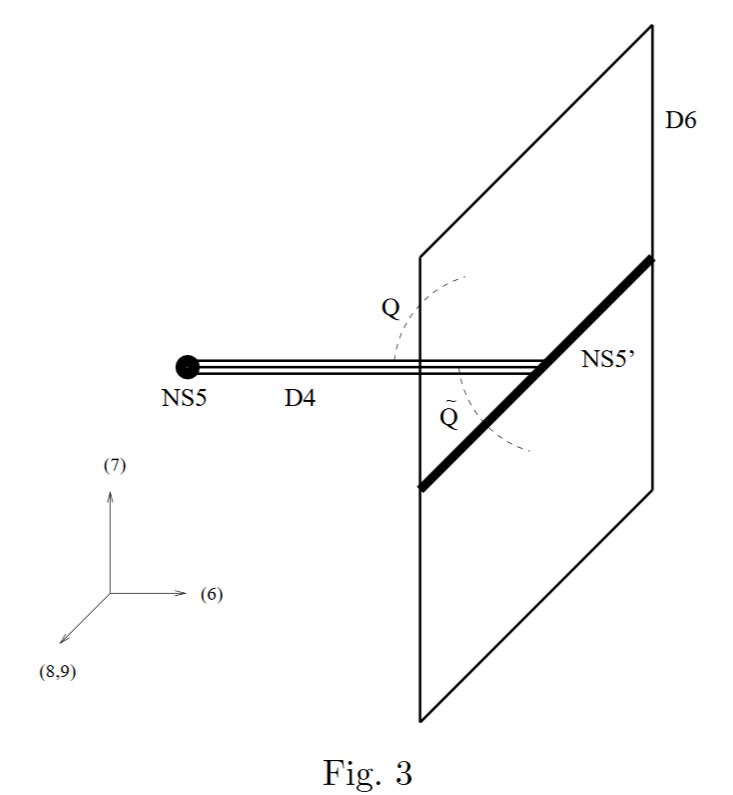
The M-theory lift is a single M5-brane branching along a Seiberg-Witten curve (see there). In the singular limit this is the intersection locus of two M5-branes on an “M3-brane” (see there).
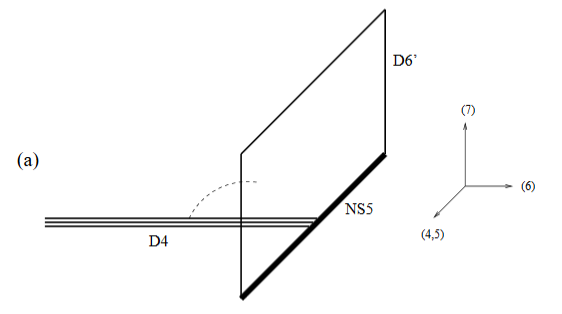
D6-branes ending on NS5-branes
Consider a black NS5-brane with near horizon geometry (EGKRS 00, p. 8):

The 3-sphere factor is the unit sphere around the black NS5-brane worldvolume , and parameterizes the radial distance from it.
Placing a D6-brane at one point of the -factor (EGKRS 00, p. 20)
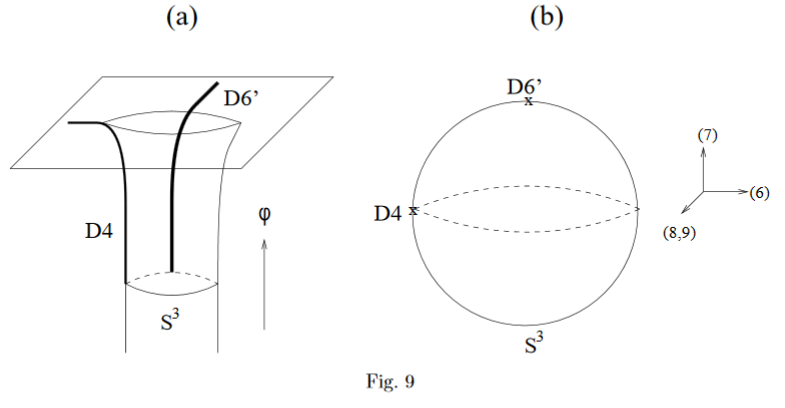
means to take its worldvolume to be the factor , hence extending to one side of the NS5-brane (EGKRS 00, p. 7):
Placing another D6-brane at the corresponding antipodal point means to have it extend also to the other side (EGKRS 00, p. 5):
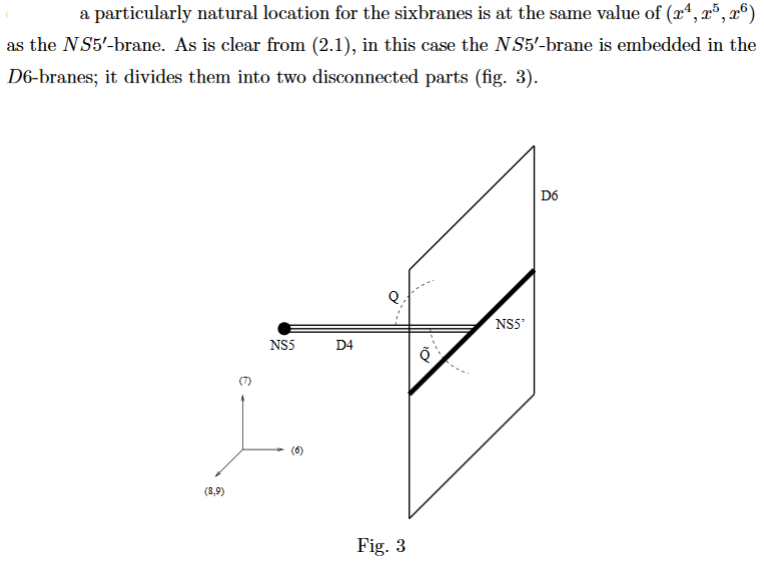
or else to have embedded the black NS5-brane into a single D6-brane.
Special properties D6-branes ending on NS5-branes were highlighted in (Brodie-Hanany 97, section 2.4): the worldvolume theory becomes chiral.
The M-theory-lift of this situation should be the 4-spherical orbifold near horizon geometry of an M5-brane (MFF 12, section 8.3)
where is a finite subgroup of SU(2) (hence in the ADE classification), acting via the identification (see at 4-sphere the section SU(2)-action). For non-trivial , this action has precisely two fixed points . Hence must be the worldvolume of two KK-monopoles of 11d supergravity, which is the M-theory lift of the two D6-branes. While the M-theory lift of the NS5-brane is the M5-brane with worldvolume . See also Fazzi 17, p. 38:
The NS5-D6 Hanany–Witten setup engineering six-dimensional theories is equivalent to M5-branes at an singularity in eleven dimensions.
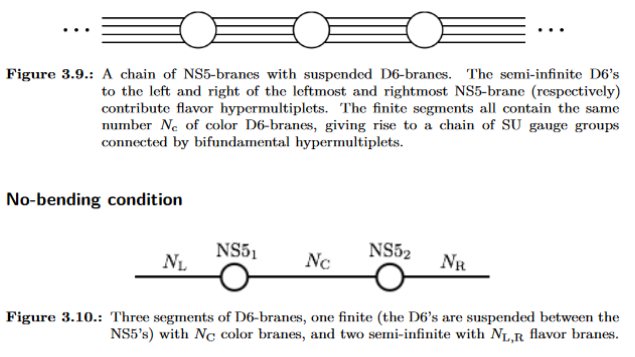
Next, this construction may be repeated, having the D6-branes end on different NS5-branes, hence “suspended between NS5-branes” (graphics from Fazzi 17, p. 33):
D6 branes intersecting D8-branes over NS5-branes
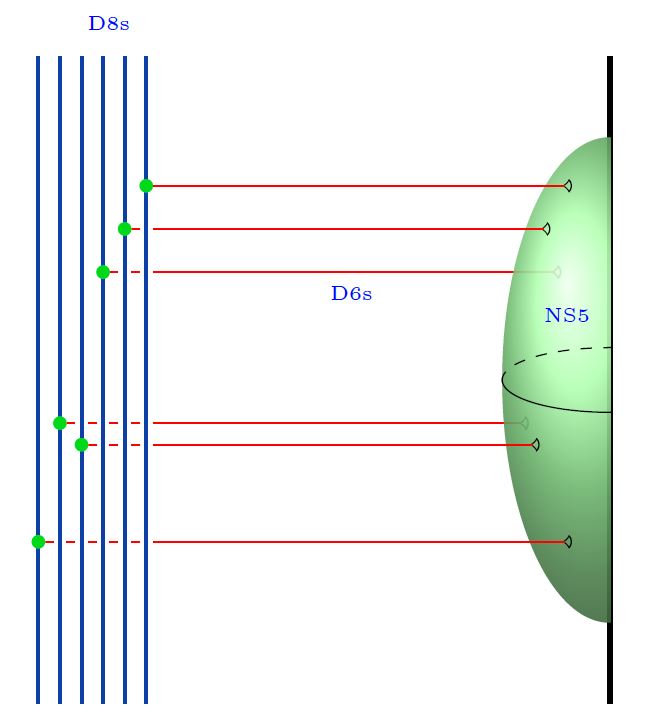
…and on the other end, the D6-branes may end on D8-branes over an NS5-brane (Janssen-Meessen-Ortin 99, Section 3) yielding D6-D8 brane intersections (for more detials see at Hanany-Witten effect, here):
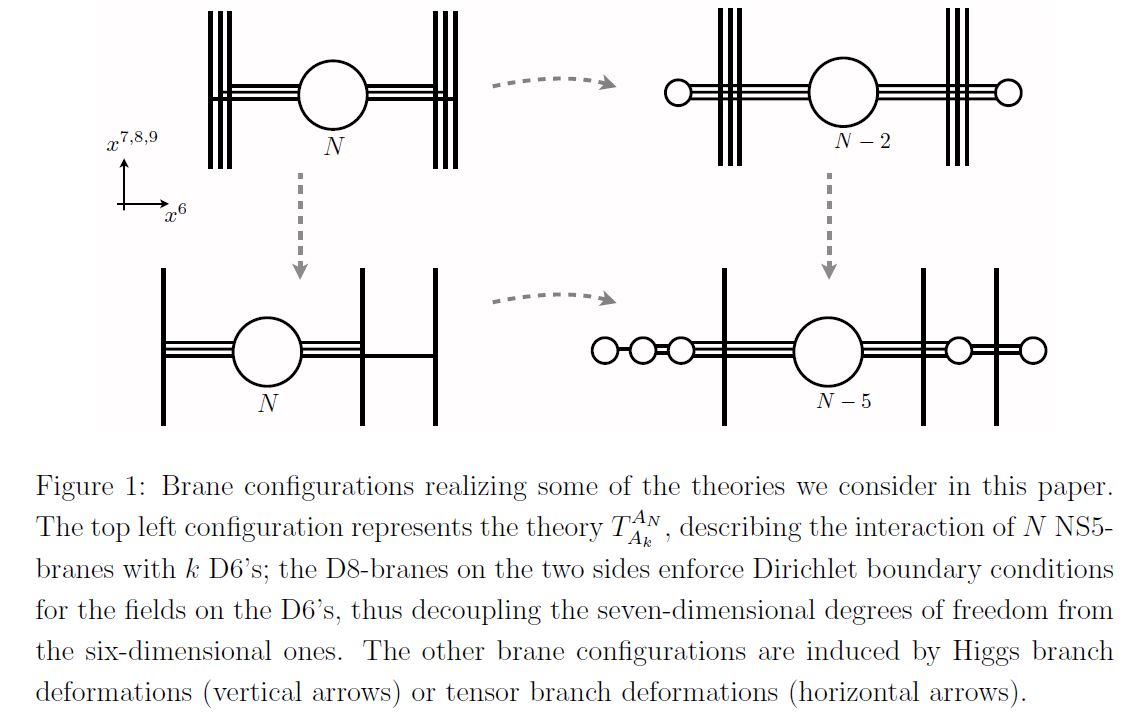
graphics grabbed from Gaiotto-Tomasiello 14
Subject to the s-rule:
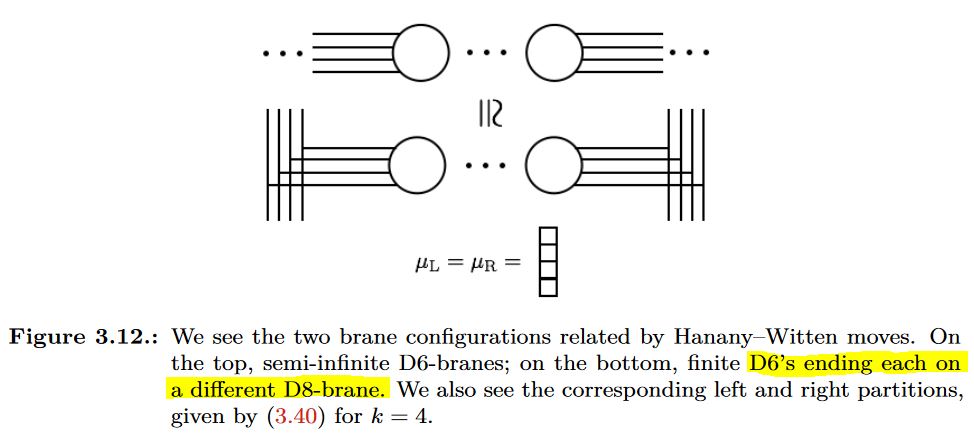
graphics grabbed from Fazzi 17
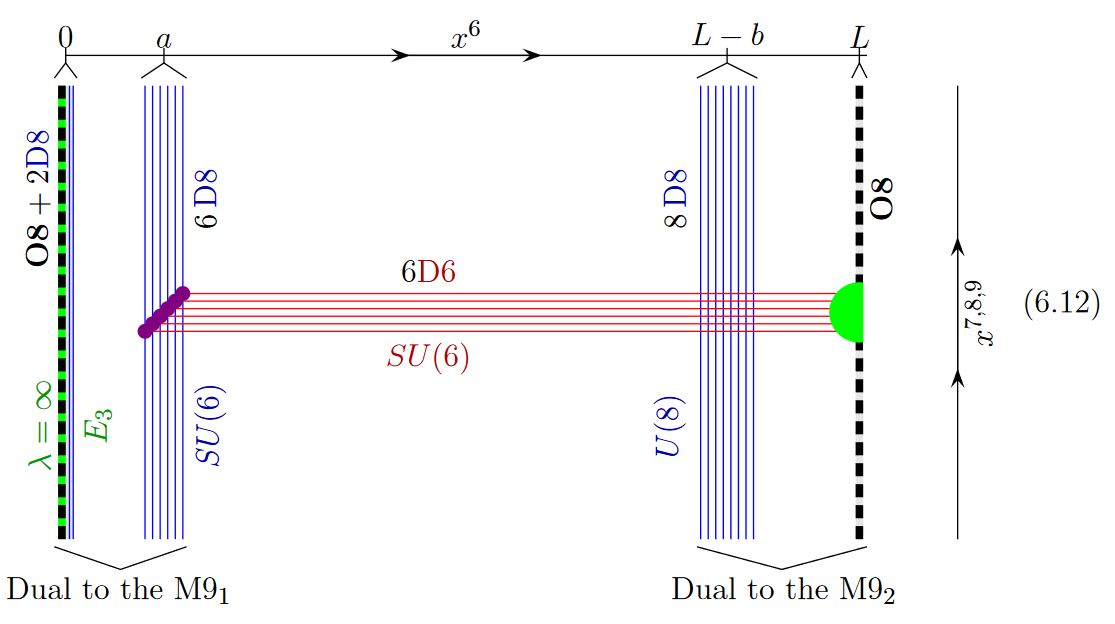
graphics grabbed from GKSTY 02
fuzzy funnelnoncommutative geometry:
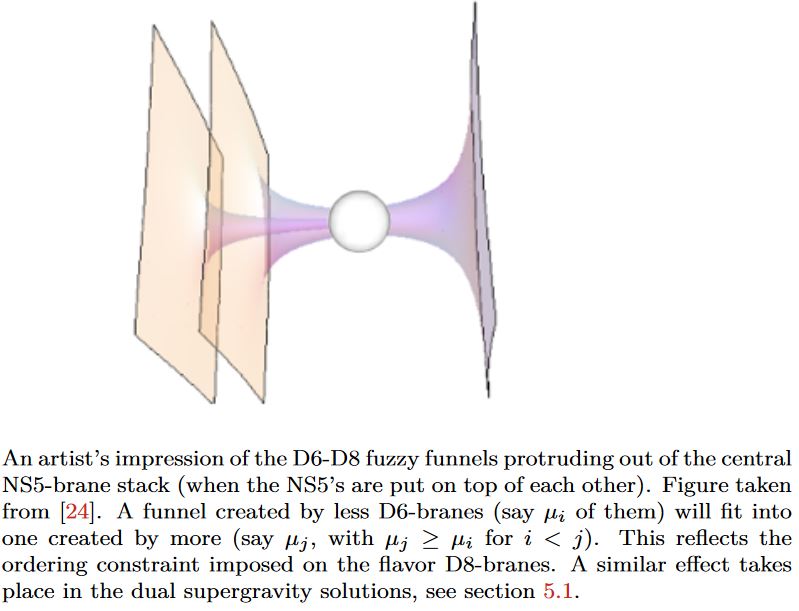
graphics grabbed from Fazzi 17, Fig. 3.14, taken in turn from Gaiotto-Tomassiello 14, Figure 5
Generally Dp-D(p+2)-brane intersections geometrically engineer Yang-Mills monopoles in the worldvolume of the higher dimensional D-branes.
Specifically for , i.e. for D6-D8-brane intersections, this fits with the Witten-Sakai-Sugimoto model geometrically engineering quantum chromodynamics, and then gives a geometric engineering of the Yang-Mills monopoles in actual QCD (HLPY 08, p. 16).
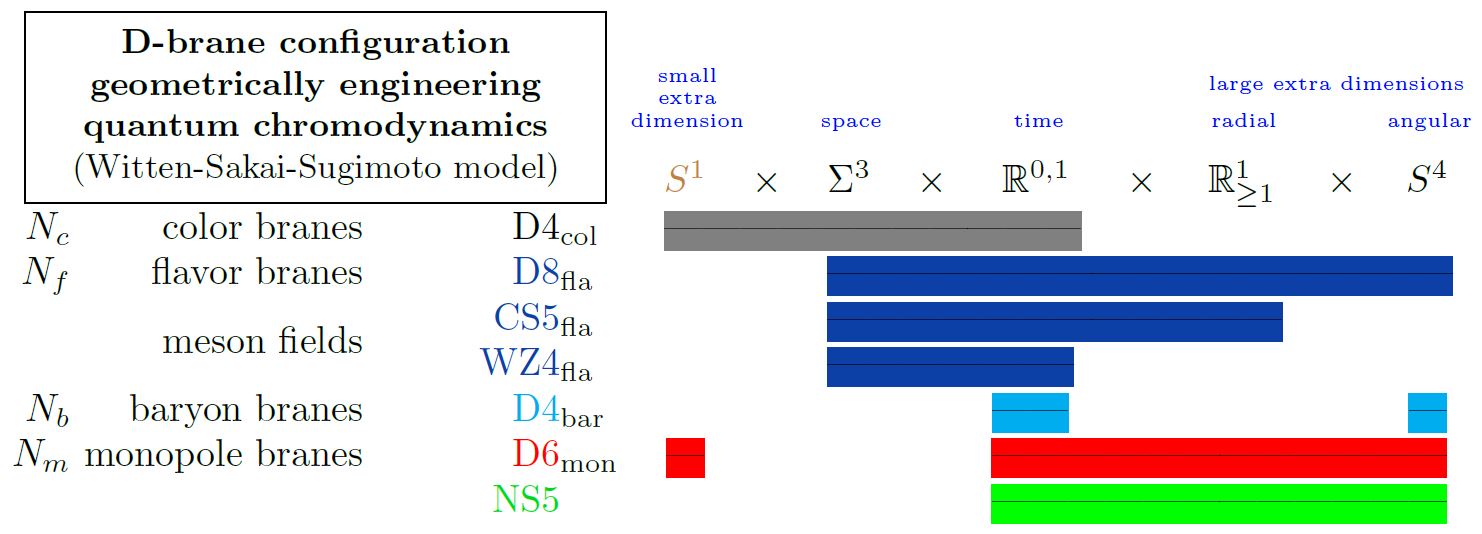
Here we are showing
-
with
-
the 5d Chern-Simons theory on their worldvolume
-
the corresponding 4d WZW model on the boundary
both exhibiting the meson fields
-
-
(see at WSS – Baryons)
-
the Yang-Mills monopole D6-branes
(see at D6-D8-brane bound state)
-
the NS5-branes.
graphics grabbed from Sati-Schreiber 20
NS5 half-branes
By the discussion above, a black D6-brane may end on a black NS5-brane, and in fact a priori each brane NS5-brane has to be the junction of two black D6-branes.
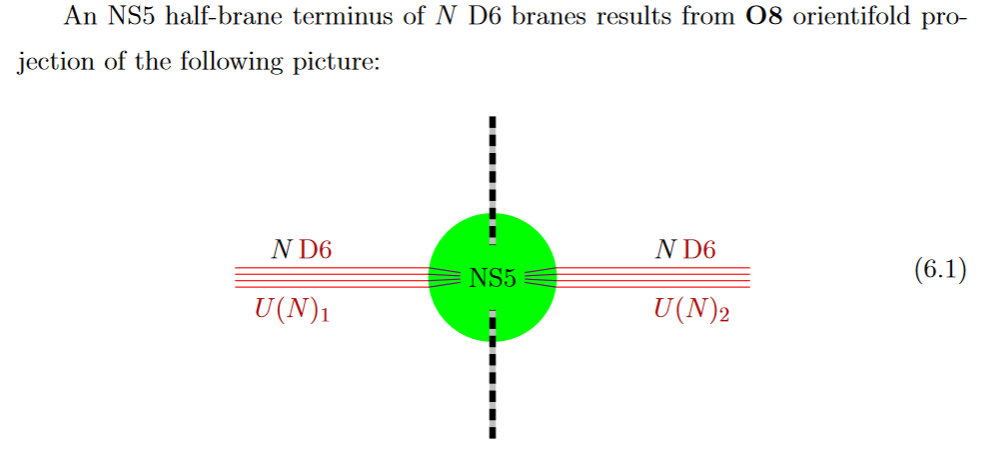
from GKSTY 02
If in addition the black NS5-brane sits at an O8-plane, hence at the orientifold fixed point-locus, then in the ordinary -quotient it appears as a “half-brane” with only one copy of D6-branes ending on it:
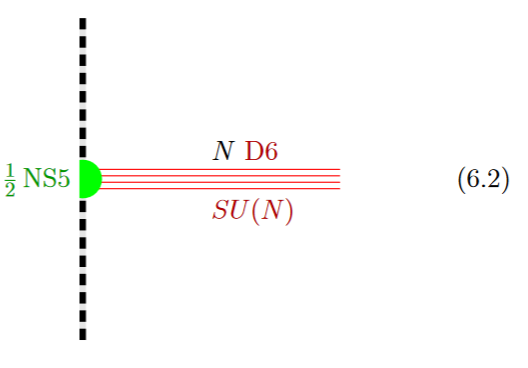
from GKSTY 02
(In Hanany-Zaffaroni 99 this is interpreted in terms of the 't Hooft-Polyakov monopole.)
The lift to M-theory of this situation is an M5-brane intersecting an M9-brane (see at MO5-plane and at heterotic M-theory on ADE-orbifolds):
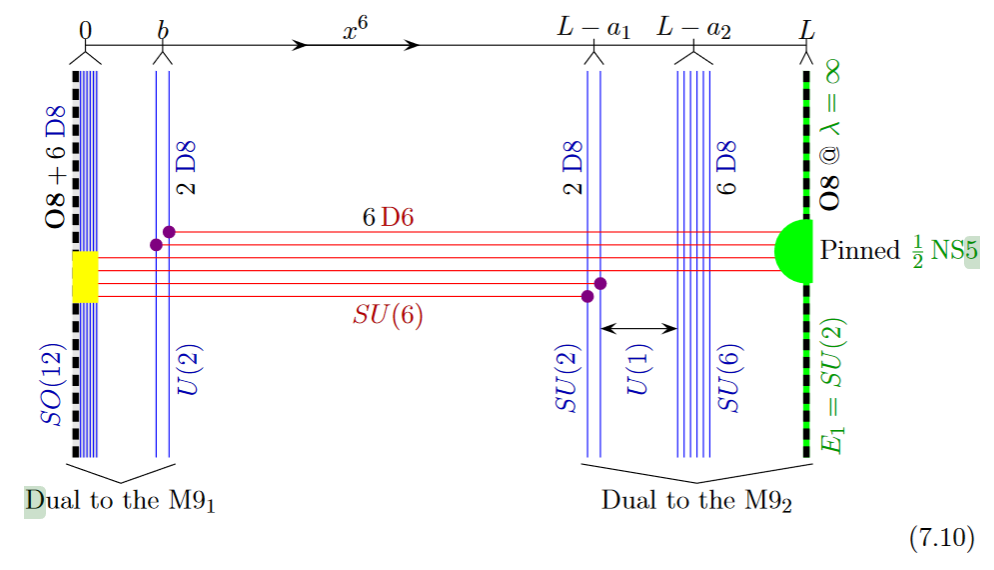
from GKSTY 02
Alternatively the O8-plane may intersect the black D6-branes away from the black NS5-brane:
from HKLY 15
In general, some of the NS5 sit away from the O8-plane, while some sit on top of it:
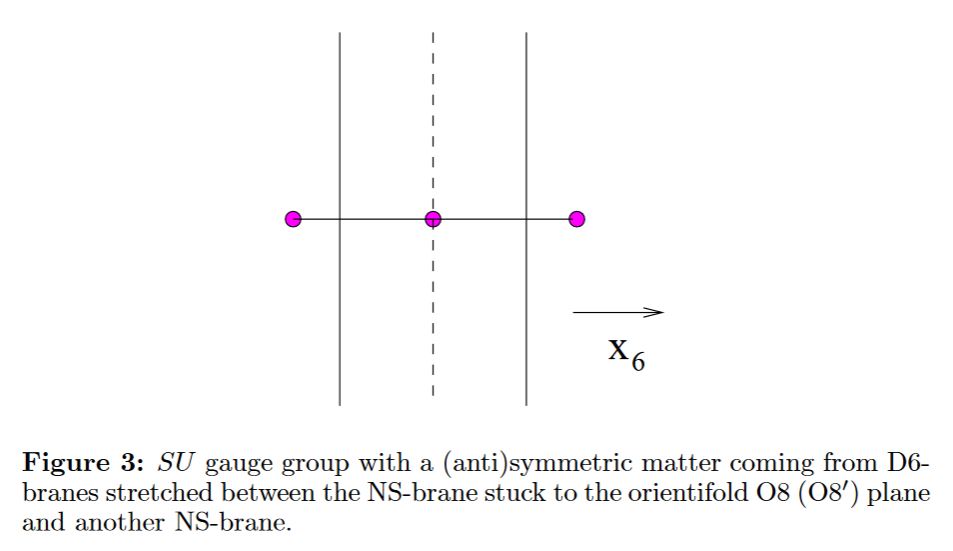
from Hanany-Zaffaroni 98

graphics grabbed from Apruzzi-Fazzi 17, p. 18
The lift to M-theory under duality between M-theory and heterotic string theory is the half M5-brane.
See also at intersecting D-brane models the section Intersection of D6s with O8s.
Webs
corresponding brane webs:
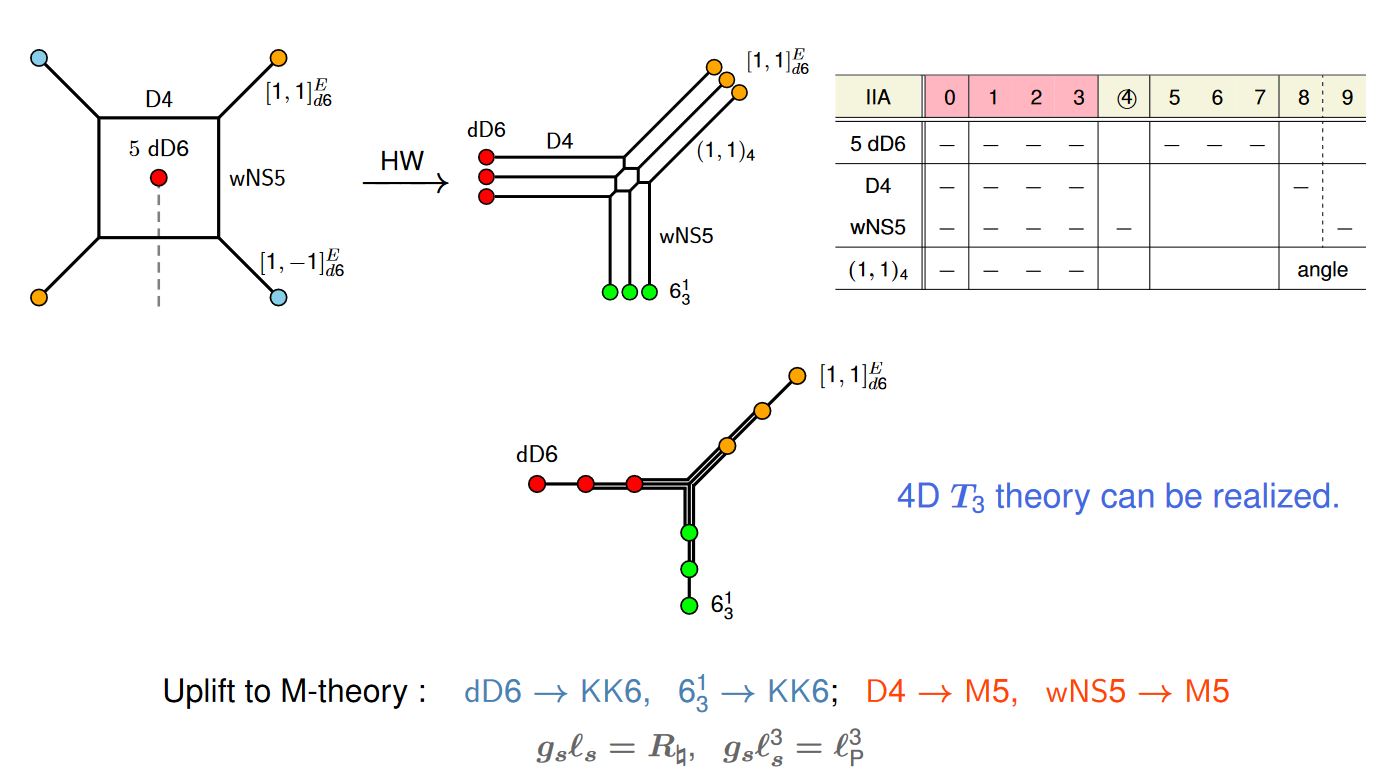
graphics grabbed from (Kimura 16 pdf)
NS5/D4/D2 bound states
bound states of NS5-branes with D4-branes and D2-branes:
Mitra-Roy 00, section 4, Mukhi-Suryanarayana 00, Jia-Lu-Roy 17, p. 12, Table 1, also Mitra-Roy 01, Alishahiha-Oz 00.
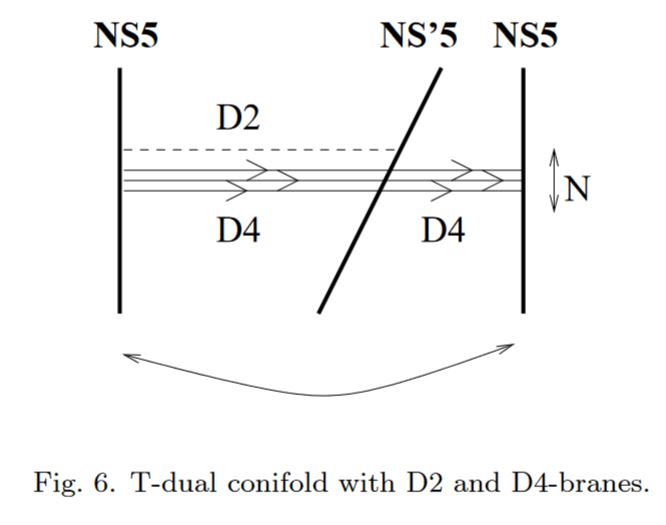
graphics grabbed from Mukhi-Suryanarayana 00
Notice that this includes configurations with the D4-branes and D2-branes contained strictly inside the NS5: Mitra-Roy 00, section 4
Review includes Camino 02, section 4.5
see also Petri 18
For the lift to M-theory see at M2-M5 brane bound state
Relation to Khovanov homology
Khovanov homology has long been expected to appear as the observables in a 4-dimensional TQFT in higher analogy of how the Jones polynomial arises as an observable in 3-dimensional Chern-Simons theory. For instance for a cobordism between two knots there is a natural morphism
between the Khovanov homologies associated to the two knots.
In (Witten11) it is argued, following indications in (GukovSchwarzVafa) that this 4d TQFT is related to the worldvolume theory of the image in type IIA of D3-branes ending on NS5-branes in type IIB after one S-duality and one T-duality operation:
Earlier indication for this had come from the observation that Chern-Simons theory is the effective background theory for the A-model 2d TCFT (see TCFT – Worldsheet and effective background theories for details).
Notice that after the above T-duality operation the -system wraps the (circle) along which the T-duality takes place.
Lifting that configuration to 11-dimensional supergravity gives M5-branes (the erstwhile D4-branes) on Taub-NUT (). The M5-branes wrap the circle-fiber of Taub-NUT, which shrinks to zero size at the origin (the location of the erstwhile D6, which is where the D4s “end”). The low-energy theory, on a stack of M5-branes, is the 6d (2,0)-susy QFT.
Related concepts
Table of branes appearing in supergravity/string theory (for classification see at brane scan).
References
As a black brane
The 5-brane in heterotic string theory was found as a black brane in
-
Heterotic solitons, Nucl.Phys. B343 (1990) 167-184 Nucl.Phys. B353 (1991) 565 (spire)
Erratum: Nucl. Phys. B353 (1991) 565-565 (doi:10.1016/0550-3213(91)90349-3, spire:27900)
-
Curtis Callan, Jeffrey Harvey, Andrew Strominger, Worldbrane actions for string solitons, Nuclear Physics B Volume 367, Issue 1, 16 December 1991, Pages 60-82 (doi:10.1016/0550-3213(91)90041-U)
-
Marco Cariglia, Kurt Lechner, NS5-branes in IIA supergravity and gravitational anomalies (arXiv:hep-th/0203238)
The intersection laws with black D-branes are discussed in
-
Arkady Tseytlin, No-force condition and BPS combinations of p-branes in 11 and 10 dimensions, Nucl.Phys.B487:141-154,1997 (arXiv:hep-th/9609212)
-
Amihay Hanany, Edward Witten, Type IIB Superstrings, BPS Monopoles, And Three-Dimensional Gauge Dynamics, Nucl. Phys. B492:152-190, 1997 (arXiv:hep-th/9611230)
-
R. Argurio, François Englert, L. Houart, Intersection Rules for -Branes, Phys. Lett. B398:61-68, 1997 (arXiv:hep-th/9701042)
-
Edward Witten, Solutions Of Four-Dimensional Field Theories Via M Theory, Nucl.Phys.B500:3-42,1997 (arXiv:hep-th/9703166)
-
John Brodie, Amihay Hanany, Type IIA Superstrings, Chiral Symmetry, and N=1 4D Gauge Theory Dualities, Nucl.Phys. B506 (1997) 157-182 (arXiv:hep-th/9704043)
-
Shmuel Elitzur, Amit Giveon, David Kutasov, Eliezer Rabinovici, Gor Sarkissian, D-Branes in the Background of NS Fivebranes, JHEP 0008 (2000) 046 [arXiv:hep-th/0005052, doi:10.1088/1126-6708/2000/08/046]
Review includes
- Marco Fazzi, Higher-dimensional field theories from type II supergravity (arXiv:1712.04447)
The M-theory-lift of the black NS5-brane embedded into a D6-brane should be the configuration from section 8.3 of
- Paul de Medeiros, José Figueroa-O'Farrill, Half-BPS M2-brane orbifolds, Adv. Theor. Math. Phys. Volume 16, Number 5 (2012), 1349-1408. (arXiv:1007.4761, Euclid)
As a Green-Schwarz sigma-model
The Green-Schwarz action functionals for the NS5-brane:
In heterotic string theory (see also at dual heterotic string theory):
-
Kurt Lechner, Mario Tonin, Worldvolume and target space anomalies in the D=10 super–fivebrane sigma–model (arXiv:hep-th/9603094)
-
J. Mourad, Anomalies of the five-brane and their cancellation, Nucl.Phys. B512 (1998) 199-208 (arxiv:hep-th/9709012)
-
Kurt Lechner, Quantum properties of the heterotic five-brane, Phys.Lett.B693:323-329, 2010 (arxiv:1005.5719)
-
Igor Bandos, Alexei Nurmagambetov, Dmitri Sorokin, The type IIA NS5–Brane (arXiv:hep-th/0003169)
-
Daniel Persson, Fivebrane Instantons and Hypermultiplets (2010) (pdf)
as a higher WZW model:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields
Under dualities
Discussion of the effect of T-duality on NS5-branes includes
-
Eduardo Eyras, Bert Janssen, Yolanda Lozano, 5-branes, KK-monopoles and T-duality, Nucl. Phys. B 531 (1998) 275-301 [arXiv:hep-th/9806169, doi:10.1016/S0550-3213(98)00575-6]
-
David Tong, NS5-Branes, T-Duality and Worldsheet Instantons, JHEP 0207:013,2002 (arXiv:hep-th/0204186)
Relation to the M5-brane
Most of the following references are more on the M5-brane.
The fact that the worldvolume theory of the M5-brane should support fields that are self-dual connections on a 2-bundle ( a gerbe) is discussed in
- Edward Witten, Conformal field theory in four and six dimensions, in Ulrike Tillmann, Topology, Geometry and Quantum Field Theory: Proceedings of the 2002 Oxford Symposium in Honour of the 60th Birthday of Graeme Segal, London Mathematical Society Lecture Note Series (2004) (arXiv:0712.0157)
as well as sections 3 and 4 of
- Edward Witten, Geometric Langlands From Six Dimensions (arXiv:0905.2720)
.
A review of some aspects is in
- Robbert Dijkgraaf, The mathematics of fivebranes (pdf)
The relation to Khovanov homology is discussed in
-
Edward Witten, Fivebranes and Knots, Quantum Topology, Volume 3, Issue 1, 2012, pp. 1-137 (arXiv:1101.3216, doi:10.4171/QT/26)
-
Sergei Gukov, Albert Schwarz, Cumrun Vafa, Khovanov-Rozansky Homology And Topological Strings , Lett. Math. Phys. 74 (2005) 53-74, (arXiv:hep-th/0412243)
See also
- Greg Moore, On the role of six‐dimensional -theories in recent developments in
Physical Mathematics_ , talk at Strings2011 (pdf slides)
The above discussion makes use of some blog comments (notably by Jacques Distler) appearing at
- Urs Schreiber, 4d QFT for Khovanov Homology (web)
Intersection with O8/D8
Intersection of black NS5-branes with O8-planes/black D8-branes is discussed in
-
Amihay Hanany, Alberto Zaffaroni, Branes and Six Dimensional Supersymmetric Theories, Nucl.Phys. B529 (1998) 180-206 (arXiv:hep-th/9712145)
-
Bert Janssen, Patrick Meessen, Tomas Ortin, The D8-Brane Tied up: String and Brane Solutions in Massive Type IIA Supergravity, Phys. Lett. B453 (1999) 229-236 (arXiv:hep-th/9901078)
-
Amihay Hanany, Alberto Zaffaroni, Monopoles in String Theory, JHEP 9912 (1999) 014 (arXiv:hep-th/9911113)
-
E. Gorbatov, Vadim Kaplunovsky, Jacob Sonnenschein, Stefan Theisen, Shimon Yankielowicz, On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015, 2002 (arXiv:hep-th/0108135)
-
Davide Gaiotto, Alessandro Tomasiello, Holography for theories in six dimensions (arXiv:1404.0711)
-
Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Futoshi Yagi, 6d SCFTs, 5d Dualities and Tao Web Diagrams, JHEP05(2019)203 (arXiv:1509.03300)
-
Fabio Apruzzi, Marco Fazzi, with orientifolds, J. High Energ. Phys. (2018) 2018: 124 (arXiv:1712.03235)
-
John Huerta, Hisham Sati, Urs Schreiber, Example 2.2.7 of: Real ADE-equivariant (co)homotopy and Super M-branes, Communications in Mathematical Physics (2019) (arXiv:1805.05987, doi:10.1007/s00220-019-03442-3)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Section 4 of: Super-exceptional geometry: origin of heterotic M-theory and super-exceptional embedding construction of M5 (arXiv:1908.00042)
On the orientifold T-dual of half M5-branes:
- Bo Feng, Yang-Hui He, Andreas Karch, Angel Uranga, Orientifold dual for stuck NS5 branes, JHEP 0106:065, 2001 (arXiv:hep-th/0103177)
For more see at M-theory on S1/G_HW times H/G_ADE.
NS5/D4/D2 bound states
bound states of NS5-branes with D4-branes and D2-branes (see also at M2-branes – Dyonic membranes)
-
Indranil Mitra, Shibaji Roy, (NS5,Dp) and (NS5,D(p+2),Dp) bound states of type IIB and type IIA string theories, JHEP 0102:026, 2001 (arXiv:hep-th/0011236)
-
Mohsen Alishahiha, Yaron Oz, Supergravity and “New” Six-Dimensional Gauge Theories, Phys.Lett.B495:418-426, 2000 (arXiv:hep-th/0008172)
-
Indranil Mitra, Shibaji Roy, (NS5,D5,D3) bound state, OD3, OD5 limits and SL(2,Z) duality, Phys.Rev. D65 (2002) 106001 (arXiv:hep-th/0107127)
-
Sunil Mukhi, Nemani V. Suryanarayana, Stable Non-BPS States and Their Holographic Duals, Int. J. Mod. Phys. A16 (2001) 966-975 (arXiv:hep-th/0011185)
-
J. M. Camino, section 4.5 of Worldvolume Dynamics of Branes (arXiv:hep-th/0210249)
-
Qiang Jia, J. X. Lu, Shibaji Roy, On 1/4 BPS ((F, D1), (NS5, D5)) bound states of type IIB string theory, JHEP 08 (2017) 007 (arXiv:1704.01463)
-
Giuseppe Dibitetto, Nicolò Petrim, 6d surface defects from massive type IIA, JHEP 01 (2018) 039 (arXiv:1707.06154)
-
Nicolò Petri, Surface defects in massive IIA, talk at Recent Trends in String Theory and Related Topics 2018 (pdf)
Open D-brane theories on the NS5
-
Rajesh Gopakumar, Shiraz Minwalla, Nathan Seiberg, Andrew Strominger, OM Theory in Diverse Dimensions, JHEP 0008:008, 2000 (arXiv:hep-th/0006062)
-
Troels Harmark, Open Branes in Space-Time Non-Commutative Little String Theory, Nucl.Phys. B593 (2001) 76-98 (arXiv:hep-th/0007147)
-
J. X. Lu, -Dimensional Open Brane Theories, JHEP 0108:049, 2001 (arXiv:hep-th/0102056)
Last revised on January 27, 2024 at 16:57:16. See the history of this page for a list of all contributions to it.