nLab orbifold
Context
Higher Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Higher Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Contents
Idea
An orbifold is much like a smooth manifold but possibly with singularities of the form of fixed points of finite group-actions.
Where a smooth manifold is a space locally modeled on Cartesian spaces/Euclidean spaces , an orbifold is, more generally, a space that is locally modeled on smooth action groupoids (homotopy quotients) of a finite group acting on a Cartesian space.
This turns out to be broadly captured (Moerdijk-Pronk 97, Moerdijk 02) by saying that an orbifold is a proper étale Lie groupoid. (Morita equivalent Lie groupoids correspond to the same orbifolds.)
The word orbifold was introduced in (Thurston 1992), while the original name was -manifold (Satake), and was taken in a more restrictive sense, assuming that the actions of finite groups on the charts are always effective. Nowadays these are called effective orbifolds and those which are global quotients by a finite group are global quotient orbifolds.
There is also a notion of finite stabilizers in algebraic geometry. A singular variety is called an (algebraic) orbifold if it has only so-called orbifold singularities.
Definition
An orbifold is a stack presented by an orbifold groupoid.
Properties
General
-
One can consider a bicategory of proper étale Lie groupoids and the orbifolds will be the objects of certain bicategorical localization of this bicategory (a result of Moerdijk-Pronk 97).
-
Equivalently, every orbifold is globally a quotient of a smooth manifold by an action of finite-dimensional Lie group with finite stabilizers in each point. (eg (Adem-Leida-Ruan 2007), Corollary 1.24)
Global quotient orbifolds
In (ALR 07, theorem 1.23) it is asserted that every effective orbifold (paracompact, Hausdorff) is isomorphic to a global quotient orbifold, specifically to a global quotient of (where is the dimension of ) acting on the frame bundle of (which is a manifold).
(Co)homology
It has been noticed that the topological invariants of the underlying topological space of an orbifold as a topological space with an orbifold structure are not appropriate, but have to be corrected leading to orbifold Euler characteristics, orbifold cohomology etc. One of the constructions which is useful in this respect is the inertia orbifold (the inertia stack of the original orbifold) which gives rise to “twisted sectors” in Hilbert space of a quantum field theory on the orbifold, and also to twisted sectors in the appropriate cohomology spaces. A further generalization gives multitwisted sectors.
Examples
-
Some basic building blocks of orbifolds:
The quotient of a ball by a discrete subgroup of the special orthogonal group of rotations is an orbifold, and orbifolds may be obtained by cutting out balls from ordinary smooth manifolds and gluing in these orbifold quotients.
-
The moduli stack of elliptic curves over the complex numbers is an orbifold, being the homotopy quotient of the upper half plane by the special linear group acting by Möbius transformations.
-
For any orbifold, then the mapping space is again an orbifold, called the inertia orbifold.
-
See also Lange 2024
Related concepts
Orbifolds are in differential geometry what Deligne-Mumford stacks are in algebraic geometry. See also at geometric invariant theory and GIT-stable point.
Orbifolds may be regarded as a kind of stratified spaces.
See also
Orbifolds in string theory:
References
General
The original articles:
-
Ichiro Satake, On a generalisation of the notion of manifold, Proc. Nat. Acad. Sci. U.S.A. 42 (1956), 359–363 (doi:10.1073/pnas.42.6.359)
-
Ichiro Satake, The Gauss–Bonnet theorem for -manifolds, J. Math. Soc. Japan 9 (1957), 464–492 (euclid:1261153826)
-
William Thurston, Three-dimensional geometry and topology, preliminary draft, University of Minnesota, Minnesota, (1992)
which in completed and revised form is available as his book:
The Geometry and Topology of Three-Manifolds; (web)
in particular the orbifold discussion is in chapter 13
-
André Haefliger, Groupoides d’holonomie et classifiants, Astérisque no. 116 (1984), p. 70-97 (numdam:AST_1984__116__70_0/)
and specifically for orbifolds in complex geometry:
-
Walter Lewis Baily, On the quotient of an analytic manifold by a group of analytic homeomorphisms, PNAS 40 (9) 804-808 (1954) (doi:10.1073/pnas.40.9.804)
-
Walter Lewis Baily, The Decomposition Theorem for V-Manifolds, American Journal of Mathematics Vol. 78, No. 4 (Oct., 1956), pp. 862-888 (jstor:2372472)
For careful comparative review of the definitions in these original articles see IKZ 10.
Survey of basic orbifold theory:
-
Daryl Cooper, Craig Hodgson, Steve Kerckhoff, Three-dimensional Orbifolds and Cone-Manifolds, MSJ Memoirs Volume 5, 2000 (pdf, euclid:1389985812)
-
Ieke Moerdijk, Janez Mrčun, Section 2.4 of: Introduction to foliations and Lie groupoids, Cambridge Studies in Advanced Mathematics 91, 2003. x+173 pp. ISBN: 0-521-83197-0 (doi:10.1017/CBO9780511615450)
-
Charles Boyer, Krzysztof Galicki, Chapter 4 of: Sasakian Geometry, Oxford Mathematical Monographs, Oxford University Press, 2007 (doi:10.1093/acprof:oso/9780198564959.001.0001)
-
Adam Kaye, Two-Dimensional Orbifolds, 2007 (pdf)
-
Michael Davis, Lectures on orbifolds and reflection groups, 2008 (pdf)
-
Joan Porti, An introduction to orbifolds, 2009 (pdf)
-
Andrew Snowden, Introduction to orbifolds, 2011 (pdf)
-
Alejandro Adem, Michele Klaus, Lectures on orbifolds and group cohomology (pdf, pdf)
-
Francisco C. Caramello Jr, Introduction to orbifolds (arXiv:1909.08699)
See also
-
Wikipedia, Orbifolds
(which is mainly tailored toward Thurston’s approach).
Additional examples:
- Christian Lange. Good, but not very good orbifolds (2024). (arXiv:2404.14234).
Textbook account:
-
John Ratcliffe, Geometric Orbifolds, chapter 13 in Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer 2006 (doi:10.1007/978-0-387-47322-2, pdf)
-
Michael Kapovich, Chapter 6 of: Hyperbolic Manifolds and Discrete Groups, Modern Birkhäuser Classics, Birkhäuser 2008 (doi:10.1007/978-0-8176-4913-5)
Application to moduli spaces of curves and moduli spaces of Riemann surfaces:
- Lizhen Ji, Shing-Tung Yau, Transformation Groups and Moduli Spaces of Curves, International Press of Boston 2011 (ISBN:9781571462237)
-
Christian Lange, Orbifolds from a metric viewpoint (arXiv:1801.03472)
-
Renato G. Bettiol, Andrzej Derdzinski, Paolo Piccione, Teichmüller theory and collapse of flat manifolds, Annali di Matematica (2018) 197: 1247 (arXiv:1705.08431, doi:10.1007/s10231-017-0723-7)
-
S. T. Hyde, S. J. Ramsden and V. Robins, Unification and classification of two-dimensional crystalline patterns using orbifolds, Acta Cryst. (2014). A70, 319-337 (doi:10.1107/S205327331400549X)
Survey of applications in mathematical physics and notably in string theory:
- Alejandro Adem, Jack Morava, Yongbin Ruan, Orbifolds in Mathematics and Physics, Contemporary Mathematics 310 American Mathematical Society, 2002
Orbifolds often appear as moduli spaces in differential geometric setting:
- Joel W. Robbin, Dietmar A. Salamon, A construction of the Deligne–Mumford orbifold, J. Eur. Math. Society 8, Nº 4 (2006) 611–699, arXiv:math/0407090 MR2009d:32012, Corrigendum, J. Eur. Math. Soc. (JEMS) 9 (2007), no. 4, 901–905, doi
The generalization of orbifolds to weighted branched manifolds is discussed in
- Dusa McDuff, Groupoids, branched manifolds and multisections, J. Symplectic Geom. Volume 4, Number 3 (2006), 259-315 (project euclid).
On orbifolds, orbifold cohomology and specifically on Chen-Ruan cohomology and orbifold K-theory:
- Alejandro Adem, Johann Leida, Yongbin Ruan, Orbifolds and Stringy Topology, Cambridge Tracts in Mathematics 171 (2007) (doi:10.1017/CBO9780511543081, pdf)
As Lie groupoids
Discussion of orbifolds as Lie groupoids/differentiable stacks:
-
Ieke Moerdijk, Dorette Pronk, Orbifolds, sheaves and groupoids, K-theory 12 3-21 (1997) (pdf, doi:10.4171/LEM/56-3-4)
-
Ieke Moerdijk, Orbifolds as Groupoids: an Introduction, in: Alejandro Adem, Jack Morava, Yongbin Ruan (eds.) Orbifolds in Mathematics and Physics, Contemporary Math 310, AMS (2002), 205–222 (arXiv:math.DG/0203100)
-
Eugene Lerman, Orbifolds as stacks?, Enseign. Math. 56 3-4 (2010) 315-363 [arXiv:0806.4160, doi:10.4171/LEM/56-3-4]
Review:
- Alexander Amenta, The Geometry of Orbifolds via Lie Groupoids, ANU 2012 (arXiv:1309.6367)
Analogous discussion for topological orbifolds as topological stacks:
- Vesta Coufal, Dorette Pronk, Carmen Rovi, Laura Scull, Courtney Thatcher, Orbispaces and their Mapping Spaces via Groupoids: A Categorical Approach, Contemporary Mathematics 641 (2015): 135-166 (arXiv:1401.4772)
Discussion of the corresponding perspective in algebraic geometry, via Deligne-Mumford stacks:
- Andrew Kresch, On the geometry of Deligne-Mumford stacks (doi:10.5167/uzh-21342, pdf), in: D. Abramovich, A. Bertram, L. Katzarkov, R. Pandharipande, M. Thaddeus (eds.) Algebraic Geometry: Seattle 2005, Proceedings of Symposia in Pure Mathematics 80, Providence, Rhode Island: American Mathematical Society 2009, 259-271 (pspum-80-1)
The mapping stacks of orbifolds are discussed in
-
Weimin Chen, On a notion of maps between orbifolds, I. Function spaces, Commun. Contemp. Math. 8 (2006), no. 5, 569–620 (arXiv:math/0603671, doi:10.1142/S0219199706002246).
-
David Roberts, Raymond Vozzo, The Smooth Hom-Stack of an Orbifold, In : Wood D., de Gier J., Praeger C., Tao T. (eds) 2016 MATRIX Annals. MATRIX Book Series, vol 1. Springer, Cham (2018) (arXiv:1610.05904, doi:10.1007/978-3-319-72299-3_3)
Discussion of principal bundles and fiber bundles over orbifolds:
-
Camille Laurent-Gengoux, Jean-Louis Tu, Ping Xu, Chern-Weil map for principal bundles over groupoids, Math. Z. 255, 451–491 (2007) (arXiv:math/0401420, doi:10.1007/s00209-006-0004-4)
-
Christopher Seaton, Characteristic Classes of Bad Orbifold Vector Bundles, Journal of Geometry and Physics 57 (2007), no. 11, 2365–2371 (arXiv:math/0606665)
An expected relation of orbifolds (orbispaces) to global equivariant homotopy theory:
- Stefan Schwede, Orbispaces, orthogonal spaces, and the universal compact Lie group (arXiv:1711.06019) (on the relation to orbispaces/topological stacks)
As diffeological spaces
On orbifolds regarded as naive local quotient spaces (instead of homotopy quotients/Lie groupoids/differentiable stacks) but as such formed in diffeological spaces:
-
Patrick Iglesias-Zemmour, Yael Karshon, Moshe Zadka, Orbifolds as diffeologies, Transactions of the American Mathematical Society 362 (2010), 2811-2831 (arXiv:math/0501093)
-
Jordan Watts, The Differential Structure of an Orbifold, Rocky Mountain Journal of Mathematics, Vol. 47, No. 1 (2017), pp. 289-327 (arXiv:1503.01740)
and as stratified diffeological spaces:
- Serap Gürer, Patrick Iglesias-Zemmour, Orbifolds as stratified diffeologies, Differential Geometry and its Applications 86 (2023) 101969 [doi:10.1016/j.difgeo.2022.101969]
On this approach seen in the broader context of cohesive higher differential geometry:
-
Hisham Sati, Urs Schreiber, Proper Orbifold Cohomology (arXiv:2008.01101)
-
David Jaz Myers, Orbifolds as microlinear types in synthetic differential cohesive homotopy type theory [arXiv:2205.15887]
Orbifold cobordism
Orbifold cobordisms are discussed in
-
K. S. Druschel, Oriented Orbifold Cobordism, Pacific J. Math., 164(2) (1994), 299-319 (doi:10.2140/pjm.1994.164.299, pdf)
-
K. S. Druschel, The Cobordism of Oriented Three Dimensional Orbifolds, Pacific J. Math., bf 193(1) (2000), 45-55.
-
Andres Angel, Orbifold cobordism (pdf)
See also at orbifold cobordism.
tangential structure on orbifolds (in the context of factorization homology):
-
Tim Weelinck, Equivariant factorization homology of global quotient orbifolds (arXiv:1810.12021, talk pdf)
-
John Pardon, Orbifold bordism and duality for finite orbispectra (arXiv:2006.12702)
In string theory
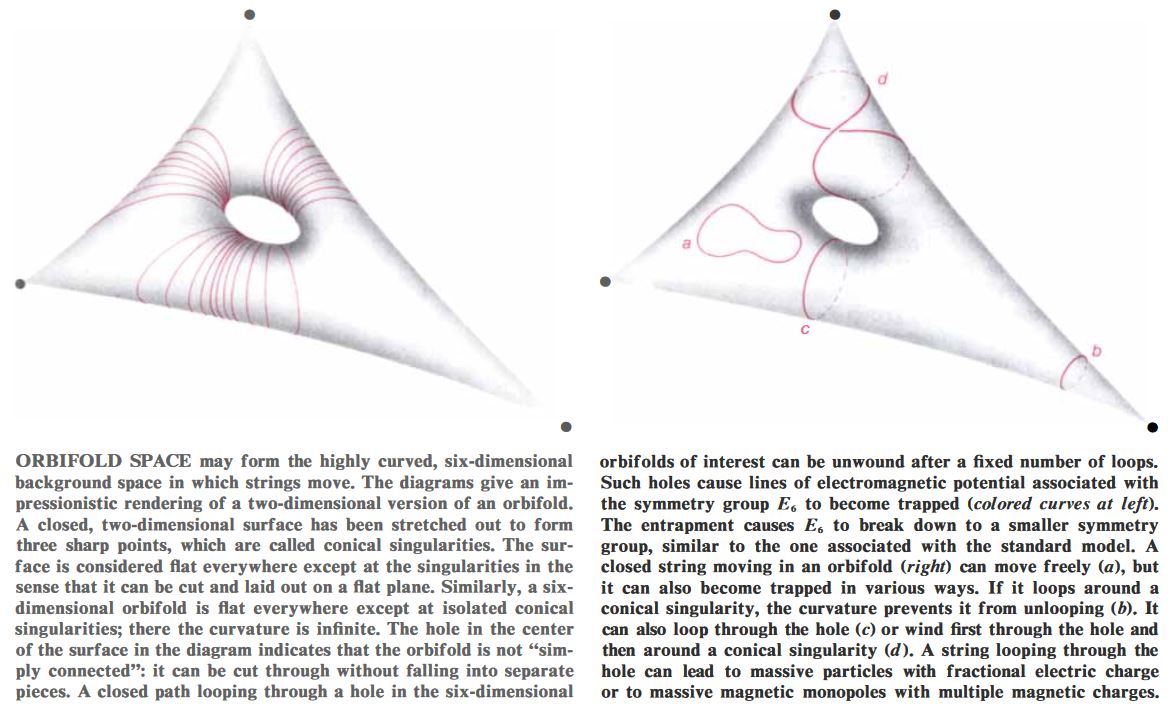
In perturbative string theory, orbifolds as target spaces for a string sigma-model were first considered in
-
Lance Dixon, Jeff Harvey, Cumrun Vafa, Edward Witten, Strings on orbifolds, Nuclear Physics B Volume 261, 1985, Pages 678-686 (doi:10.1016/0550-3213(85)90593-0)
-
Lance Dixon, Jeff Harvey, Cumrun Vafa, Edward Witten, Strings on orbifolds (II), Nuclear Physics B Volume 274, Issue 2, 15 September 1986, Pages 285-314 (doi:10.1016/0550-3213(86)90287-7)
and then further developed notably in
-
Robbert Dijkgraaf, Cumrun Vafa, Erik Verlinde, Herman Verlinde, The operator algebra of orbifold models, Comm. Math. Phys. Volume 123, Number 3 (1989), 485-526 (euclid:1104178892)
-
Eric Zaslow, Topological orbifold models and quantum cohomology rings, Comm. Math. Phys. 156 (1993), no. 2, 301–331.
See also:
- Stefano Giaccari, Roberto Volpato, A fresh view on string orbifolds [arXiv:2210.10034]
Discussion of blow-up of orbifold singularities in string theory:
- Paul Aspinwall, Resolution of Orbifold Singularities in String Theory (arXiv:hep-th/9403123)
In terms of vertex operator algebras:
- Yi-Zhi Huang, Representation theory of vertex operator algebras and orbifold conformal field theory (arXiv:2004.01172)
For orbifolds in string theory see also the references at
Review of orbifolds in the context of string KK-compactifications and intersecting D-brane models:
-
D. Bailin, A. Love, Orbifold compactifications of string theory, Phys. Rept. 315 (1999) 285-408 (doi:10.1016/S0370-1573(98)00126-4, spire:504382)
-
Katrin Wendland, Orbifold Constructions of K3: A Link between Conformal Field Theory and Geometry, in Orbifolds in Mathematics and Physics (arXiv:hep-th/0112006)
-
Joel Giedt, Heterotic Orbifolds (arXiv:hep-ph/0204315)
-
Dieter Lüst, S. Reffert, E. Scheidegger, S. Stieberger, Resolved Toroidal Orbifolds and their Orientifolds, Adv.Theor.Math.Phys.12:67-183, 2008 (arXiv:hep-th/0609014)
-
Susanne Reffert, The Geometer’s Toolkit to String Compactifications, lectures at String and M theory approaches to particle physics and cosmology, 2007 (arXiv:0706.1310)
-
Luis Ibáñez, Angel Uranga, Chapter 8 of String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012 (doi:10.1017/CBO9781139018951)
-
Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, Chapter 10.5 Toroidal orbifolds, of Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics pp 585-639 Springer 2013
and for orbifolds of G2-manifolds for M-theory on G2-manifolds:
-
Bobby Acharya, M theory, Joyce Orbifolds and Super Yang-Mills, Adv. Theor. Math. Phys. 3 (1999) 227-248 [arXiv:hep-th/9812205]
-
Frank Reidegeld, -orbifolds from K3 surfaces with ADE-singularities [arXiv:1512.05114]
-
Frank Reidegeld, -orbifolds with ADE-singularities [pdf]
and for heterotic string phenomenology:
- Saul Ramos-Sanchez, Michael Ratz, Heterotic Orbifold Models, in Handbook of Quantum Gravity, Springer (2024) [arXiv:2401.03125, doi:10.1007/978-981-19-3079-9]
For topological strings the path integral as a pull-push transform for target orbifolds – in analogy to what Gromov-Witten theory is for Deligne-Mumford stacks – has first been considered in
-
Weimin Chen, Yongbin Ruan, Orbifold Gromov-Witten Theory, in Orbifolds in Mathematics and Physics (Madison, WI, 2001), 25–85, Contemp. Math., 310, Amer. Math. Soc., Providence, RI, 2002 (arXiv:math/0103156)
A review with further pointers is in
-
Dan Abramovich, Lectures on Gromov-Witten invariants of orbifolds (arXiv:math/0512372)
On orbifolds by 2-groups in view of sigma-models inspired from string theory:
- Alonso Perez-Lona, Eric Sharpe, Three-dimensional orbifolds by 2-groups [arXiv:2303.16220]
Last revised on April 23, 2024 at 09:12:49. See the history of this page for a list of all contributions to it.