nLab groupoid
This page is about the notion of groupoids prevalent in category theory and homotopy theory, also known as Brandt groupoids (Brandt (1927)). For the notion involving a globally defined binary operation, see magma.
Context
Algebra
Algebraic theories
Algebras and modules
Higher algebras
-
symmetric monoidal (∞,1)-category of spectra
Model category presentations
Geometry on formal duals of algebras
Theorems
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Contents
Idea
Where a group may be thought of as a group of symmetry transformations that isomorphically relates one object to itself (the symmetries of one object, such as the isometries of a polyhedron) a groupoid is a collection of symmetry transformations acting between possibly more than one object.
Hence a groupoid consists of a set of objects and for each pair of objects there is a set of transformations, usually denoted by arrows
which may be composed if they are composable (i.e. if the first ends where the second starts)
such that this composition is associative
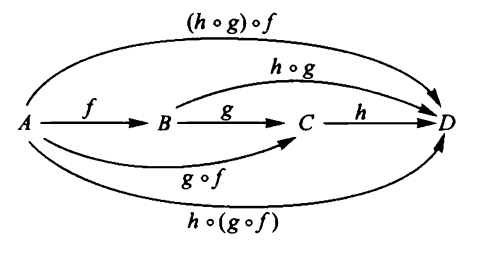
and such that for each object there is identity transformation in that this is a neutral element for the composition of transformations, whenever defined.
So far this structure is what is called a small category. What makes this a (small) groupoid is that all these transformations are to be “symmetries” in that they are invertible morphisms meaning that for each transformation there is a transformation the other way around such that
If there is only a single object , then this definition reduces to that of a group, and in this sense groupoids are “groups with many objects”. Conversely, given any groupoid and a choice of one of its objects , then the subcollection of transformations from and to is a group, sometimes called the automorphism group of in .
Just as for groups, the “transformations” above need not necessarily be given by concrete transformations (say by bijections between objects which are sets). Just as for groups, such a concrete realization is always possible, but is an extra choice (called a representation of the groupoid). Generally one calls these “transformations” morphisms: is a morphism with “source” and “domain” .
An archetypical example of a groupoid is the fundamental groupoid of a topological space (def. below, for introduction see here): For a topological space, this is the groupoid whose
-
objects are the points ;
-
morphisms are the homotopy relative boundary-equivalence classes of paths in , with and ;
and composition is given, on representatives, by concatenation of paths. Here the class of the reverse path constitutes the inverse morphism, making this a groupoid.
If one chooses a point , then the corresponding group at that point is the fundamental group of at that point.
This highlights one of the reasons for being interested in groupoids over groups: Sometimes this allows to avoid unnatural ad-hoc choices and it serves to streamline and simplify the theory.
A homomorphism between groupoids is the obvious: a function between their underlying objects together with a function between their morphisms which respects source and target objects as well as composition and identity morphisms. If one thinks of the groupoid as a special case of a category, then this is a functor. Between groupoids with only a single object this is the same as a group homomorphism.
For example if is a continuous function between topological spaces, then postcomposition of paths with this function induces a groupoid homomorphism between the fundamental groupoids from above.
Groupoids with groupoid homomorphisms (functors) between them form a category Grpd (def. below) which includes the categeory Grp of groups as the full subcategory of the groupoids with a single object. This makes precise how groupoid theory is a generalization of group theory.
However, for groupoids more than for groups one is typically interested in “conjugation actions” on homomorphisms. These are richer for groupoids than for groups, because one may conjugate with a different morphism at each object. If we think of groupoids as special cases of categories, then these “conjugation actions on homomorphisms” are natural transformations between functors.
For examples if are two continuous functions between topological spaces, and if is a homotopy from to , then the homotopy relative boundary classes of the paths constitute a natural transformation between in that for all paths in we have the “conjugation relation”
One may take care of the existence of these conjugation actions/natural transformation in two ways:
-
If one quotients them out, i.e. if one identifies two groupoid homomorphisms that differ by a conjugation action, then the resulting category of groupoids and classes of homomorphisms is called the homotopy category of Grpd (def. below). This is equivalent to the full subcategory of the classical homotopy category of topological spaces on those that are (CW-complexes and) homotopy 1-types, i.e. those for which the fundamental groupoid is the only homotopy invariant, with all higher homotopy groups being trivial:
This means that the concept of groupoids may be regarded as a combinatorial model for homotopy 1-types in homotopy theory, in contrast to the models by topological spaces given by topological homotopy theory. This equivalence generalizes to homotopy n-types as one passes to n-groupoids and eventually to all homotopy types as one passes to infinity-groupoids.
-
Instead of forgetting all the information encoded in the conjugations/natural transformations, one may also collect it all into the structure of a 2-category Grpd (in fact a (2,1)-category). As such this is the sub-2-category of Cat on those (small) categories all whose morphisms are invertible morphism.
For more introduction on this see at geometry of physics – homotopy types.
In either of these two cases, beware that the category Grp of groups is not a full subcategory either of the homotopy category or of the (2,1)-category Grpd, because conjugation action is is not part of the definition of . Instead in homotopy theory it is pointed one-object groupoids which are equivalent to groups
(Even though there is a unique choice of point for a one-object groupoid, the respect for this (unique) choice forces the conjugation actions on groupoids to be trivial. ) This simple statement is in fact a special case of the May recognition theorem (see there) which holds for more general homotopy types and even for directed homotopy types.
The equivalence of groupoids with homotopy 1-types shows immediately that, with homotopy taken into accont, the difference between groupoids and groups is rather mild, after all: Every groupoid is equivalent (isomorphic in ) to a disjoint union of groupoids with a single object (prop. below). In particular groupoid representations are equivalently just tuples of group representations (prop. below.) This is the reason why the competition between general topology textbooks that do and that do not prefer the fundamental groupoid over the fundamental group remains inconclusive.
However, this equivalence of groupoids with disjoint unions of groups depends on the axiom of choice. Even if this is assumed in the underlying foundations/set theory, it breaks once one considers groupoids equipped with geometric structure:
Just as one may consider topological groups and Lie groups, etc., there are the evident concepts of topological groupoids and Lie groupoids etc. (generally: internal groupoids). Their theory turns out to be genuinely richer than that of their group analogs, due to the interaction between the geometry and the homotopy theory (“higher geometry”).
The correct concept of homomorphisms between Lie groupoids for instance goes by many names, including Morita morphisms, Hilsum-Skandalis morphisms and bibundles. The general way to understand this and all other geometric groupoid theory is via the concept of stacks of groupoids. For more pointers on this see at higher geometry and for introduction in the case of higher differential geometry see at geometry of physics – smooth homotopy types.
Definition
Groupoids
Definition
(groupoid – homotopily typed definition)
A small groupoid is a space or homotopy type such that for all points and in , all paths and in the path space (type) , all homotopies (2-paths) and in the path space type , the path space type is contractible.
Definition
(groupoid – dependently typed definition)
A small groupoid is
-
for all pairs of objects a set , to be called the set of morphisms with domain or source and codomain or target ;
-
for all triples of objects a function
to be called composition
-
for all objects an element
to be called the identity morphism on ;
-
for all pairs of objects a function
to be called the inverse-assigning function
such that
-
(associativity) for all quadruples of objects and all triples of morphisms , and an equality
-
(unitality) for all pairs of objects and all moprhisms equalities
-
(invertibility) for all pairs of objects and every morphism equalities
If are two groupoids, then a homomorphism or functor between them, denoted
is
-
a function between the respective sets of objects;
-
for each pair of objects a function
between sets of morphisms
such that
-
(respect for composition) for all triples and all and an equality
-
(respect for identities) for all an equality
For two groupoids, and for two groupoid homomorphisms/functors, then a conjugation or homotopy or natural transformation (necessarily a natural isomorphism)
is
- for each object of a morphism
such that
-
for all and an equality
For two groupoids and three functors between them and and conjugation actions/natural isomorphisms between these, there is the composite
with components the composite of the components
This yields for any two groupoid a hom-groupoid
whose objects are the groupoid homomorphisms / functors, and whose morphisms are the conjugation actions / natural transformations.
Remark
(groupoids are special cases of dagger categories)
A small groupoid (def. ) is equivalently a small dagger category? in which all morphisms are unitary.
Remark
(groupoids are special cases of categories)
A small groupoid (def. ) is equivalently a small category in which all morphisms are isomorphisms.
Remark
(Higher groupoid theory vs higher category theory) Due to the two preceding remarks, groupoid theory may be regarded as a special case of dagger category theory? or category theory, it is noteworthy that the two theories are quite different in character. For example higher groupoid theory is homotopy theory which is rich but quite tractable, for instance via tools such as simplicial homotopy theory or homotopy type theory, while higher category theory and higher dagger category theory is intricate and becomes tractable mostly by making recourse to higher groupoid theory in the guise of (infinity,1)-category theory and (infinity,n)-categories.
Definition
(groupoid – global definition)
A small groupoid is
Remark
(Notation and Terminology)
If are objects (also called vertices) of the groupoid then the set of morphisms (also called arrows) from to is written , or other notations for hom-sets. The set (which is a group under composition) is also written and called the vertex group of at . It is also written and called the automorphism group of in , or written and called the fundamental group of at (especially if you think of a groupoid as giving a homotopy 1-type).
As in any category, there is a question of notation for the composition, and in particular of the order in which to write things. It can be more convenient to write the composition of and as , although a more traditional notation would be . The two conventions can be distinguished by writing or (which is the most traditional notation for categories). See composition for further discussion.
A groupoid is connected, or transitive?, if is nonempty for all ; it is called inhabited?, or nonempty, if it has at least one object. A maximal inhabited connected subgroupoid? of is called a component of , and is then the disjoint union (the coproduct in ) of its connected components. The set of components of is written (especially if you think of a groupoid as giving a homotopy 1-type).
Categories of groupoids
But since this 1-category does not reflect the existence of homotopies/natural isomorphisms between homomorphsims/functors of groupoids (def. ) this 1-category is not what one is interested in when considering homotopy theory/higher category theory.
In order to obtain the right notion of category of groupoids that does reflect homotopies, we first consider now the horizontal composition of homotopies/natural transformations.
Lemma
(horizontal composition of homotopies with morphisms)
Let , , , be groupoid and let
be morphisms and a homotopy . Then there is a homotopy
between the respective composites, with components given by
This operation constitutes a groupoid homomorphism/functor
Proof
The respect for identities is clear. To see the respect for composition, let
be two composable homotopies. We need to show that
Now for any object of we find
Here all steps are unwinding of the definition of horizontal and of ordinary (vertical) composition of homotopies, except the third equality, which is the functoriality of .
Lemma
(horizontal composition of homotopies)
Consider a diagram of groupoids, groupoid homomorphsims (functors) and homotopies (natural transformations) as follows:
The horizontal composition of the homotopies to a single homotopy of the form
may be defined in temrs of the horizontal composition of homotopies with morphisms (lemma ) and the (“vertical”) composition of homotopies with themselves, in two different ways, namely by decomposing the above diagram as
or as
In the first case we get
while in the second case we get
These two definitions coincide.
Proof
For an object of , then we need that the following square diagram commutes in
But the ommutativity of the square on the right is the defining compatibility condition on the components of applied to the morphism in .
Proposition
(horizontal composition with homotopy is natural transformation)
Consider groupoids, homomorphisms and homotopies of the form
Then horizontal composition with the homotopies (lemma ) constitutes a natural transformation between the functors of horizontal composition with morphisms (lemma )
It first of all follows that the following makes sense
Definition
(homotopy category of groupoids)
There is also the homotopy category whose
-
objects are small groupoids;
-
morphisms are equivalence classes of groupoid homomorphisms modulo homotopy (i.e. functors modulo natural transformations).
This is usually denoted .
Of course what the above really means is that, without quotienting out homotopies, groupoids form a 2-category, in fact a (2,1)-category, in fact an enriched category which is enriched over the naive 1-category of groupoids from remark , hece a strict 2-category with hom-groupoids.
Equivalences of groupoids
Definition
Given two groupoids and , then a homomorphism
is an equivalence if it is an isomorphism in the homotopy category (def. ), hence if there exists a homomorphism the other way around
and a homotopy/natural transformations of the form
Definition
(connected components of a groupoid)
Given a groupoid with set of objects , then the relation “there exists a morphism from to ”, i.e.
is clearly an equivalence relation on . The corresponding set of equivalence classes is denoted
and called the set of connected components of .
Definition
Given a groupoid and an object , then under composition the set forms a group. This is called the automorphism group or vertex group or isotropy group of in .
Definition
(weak homotopy equivalence of groupoids)
Let and be groupoids. Then a morphism (functor)
is called a weak homotopy equivalence if
-
it induces a bijection on connected components (def. ):
-
for each object of the morphism
is an isomorphism of automorphism groups (def. )
Groupoid representations
Definition
Let be a groupoid. Then:
A linear representation of is a groupoid homomorphism (functor)
to the groupoid core of the category Vect of vector spaces (example ). Hence this is
-
For each object of a vector space ;
-
for each morphism of a linear map
such that
-
(respect for composition) for all composable morphisms in the groupoid we have an equality
-
(respect for identities) for each object of the groupoid we have an equality
Similarly a permutation representation of is a groupoid homomorphism (functor)
to the groupoid core of Set. Hence this is
such that composition and identities are respected, as above.
For and two such representations, then a homomorphism of representations
is a natural transformation between these functors, hence is
-
for each object of the groupoid a (linear) function
-
such that for all morphisms we have
Representations of and homomorphisms between them constitute a category, called the representation category .
Examples
Example
Let be a topological space. For two points, write for the set of paths in from to . Consider the equivalence relation “homotopy relative boundary” on this set and write
for the set of equivalence classes under this relation. The concatenation of paths descends to these equivalence classes. This yields a groupoid with set of objects the set of points in the topological space. This is the called the fundamental groupoid of .
This construction extends to a functor
from the 1-category Top to the 1-category Grpd. In fact it extends to a functor
Example
((2,1)-functoriality of fundamental groupoid)
If and are topological spaces and is a continuous function between them, then this induces a groupoid homomorphism (functor) between the respective fundamental groupoids (def. )
given on objects by the underlying function of
and given on the class of a path by the evident postcomposition with
This construction clearly respects identity morphisms and composition and hence is itself a functor of the form
from the category Top of topological space to the 1-category Grpd of groupoids.
But more is true: If are two continuous function and
is a left homotopy between them, hence a continuous function
such that and , then this induces a homotopy between the above groupoid homomorphisms (a natural transformation of functors).
This shows that the fundamental groupoid functor in fact descends to homotopy categories
(In fact this means it even extends to a (2,1)-functor from the (2,1)-category of topological spaces, continuous functions, and higher homotopy-classes of left homotopues, to that of groupoids.)
As a direct consequence it follows that if there is a homotopy equivalence
between topological spaces, then there is an induced equivalence of groupoids betwee their fundamental groupoids
Hence the fundamental groupoid is a homotopy invariant of topological spaces. Of course by prop. the fundamental groupoid is equivalent, as a groupoid, to the disjoint union of the deloopings of all the fundamental groups of the given topological spaces, one for each connected component, and hence this is equivalently the statement that the set of connected components and the fundamental groups of a topological space are homotopy invariants.
Example
For any set, there is the discrete groupoid , whose set of objects is and whose only morphisms are identity morphisms.
This is also the fundamental groupoid (example ) of the discrete topological space on the set .
Example
For any set, there is the codiscrete groupoid , whose set of objects is and whose homsets are singletons. In other words, it is a groupoid where every object is uniquely isomorphic to every object.
Example
Let be a group. Then there is a groupoid, denoted , with a single object , with morphisms
the elements of , with composition the multiplication in , with identity morphism the neutral element in and with inverse morphisms the inverse elements in .
This is also called the delooping of (because the loop space object of at the unique point is the given group: ).
For two groups, then there is a natural bijection between group homomorphisms and groupoid homomorphisms : the latter are all of the form , with uniquely fixed and .
This means that the construction is a fully faithful functor
into from the category Grp of groups to the 1-category of groupoids.
But beware that this functor is not fully faithful when homotopies of groupoids are taken into acount, because there are in general non-trivial homotopies between morphims of the form
By definition, such a homotopy (natural transformation) is a choice of a single elemet such that for all we have
hence such that
Therefore notably the induced functor
to the homotopy category of groupoids is not fully faithful.
But since is canonically a pointed object in groupoids, we may also regard delooping as a functor
to the category of pointed objects of Grpd. Since groupoid homomorphisms necessarily preserve the basepoint, this makes no difference at this point. But as we now pass to the homotopy category
then also the homotopies are required to preserve the basepoint, and for homotopies between homomorphisms between delooped groups this means, since there only is a single point, that these homotopies are all trivial. Hence regarded this way the functor is a fully faithful functor again, hence an equivalence of categories onto its essential image. By prop. below this essential image consists precisely of the (pointed) connected groupoids:
Groups are equivalently pointed connected groupoids.
Example
(disjoint union/coproduct of groupoids)
Let be a set of groupoids. Then their disjoint union (coproduct) is the groupoid
whose set of objects is the disjoint union of the sets of objects of the summand groupoids, and whose sets of morphisms between two objects is that of if both objects are form this groupoid, and is empty otherwise.
Example
(disjoint union of delooping groupoids)
Let be a set of groups. Then there is a groupoid which is the disjoint union groupoid (example ) of the delooping groupoids (example ).
Its set of objects is the index set , and
Example
For any (small) category, then there is a maximal groupoid inside
sometimes called the core of . This is obtained from simply by discarding all those morphisms that are not isomorphisms.
For instance
-
For Set then is the goupoid of sets and bijections between them.
For FinSet then the skeleton of this groupoid (prop. ) is the disjoint union of deloopings (example ) of all the symmetric groups:
-
For Vect then is the groupoid of vector spaces and linear bijections between them.
For FinDimVect then the skeleton of this groupoid is the disjoint union of delooping of all the general linear groups
Example
(groupoid representation of delooping groupoid is group representation)
If is the delooping groupoid of a group (example ), then a groupoid representation of according to def. is equivalently a group representation of the group :
Here is some further examples that should be merged into the above text.
-
From any action of a group on a set we obtain an action groupoid or “weak quotient” . This is also written , a semidirect product, since it is a special case of the semidirect product of an action of a groupoid on a groupoid. If this gives the groupoid , above.
-
A symmetric proset, that is a set equipped with an equivalence relation , becomes a groupoid with the multiplication for all . (This gives one reason for the forward notation for composition.) Such a groupoid is equivalent to the discrete category on the quotient set .
-
In particular, if is the universal relation , then we get the square groupoid? , also called the trivial groupoid? on . Despite the latter name, there is an important special case, namely the groupoid . This groupoid has non-identity elements , and can be regarded as a groupoid model of the unit interval in topology.
-
More generally, if we choose some subset of the points of a space , then we have a full subgroupoid of containing only those points in , denoted . This can result in much more manageable groupoids; for instance is the groupoid considered above, while has uncountably many objects (but is equivalent to ).
-
If is a directed graph or quiver, then the free groupoid is well defined. It is the left adjoint functor to the forgetful functor from groupoids to directed graphs. This shows an advantage of groupoids: the notion of free equivalence relation or free action groupoid does not easily make sense. But we can still talk of a presentation of an equivalence relation or action groupoid by generators and relations, by considering presentations of groupoids instead.
-
A paper by Živaljević gives examples of groupoids used in combinatorics.
-
The book “Topology and Groupoids” listed below takes the view that 1-dimensional homotopy theory, including the Seifert-van Kampen Theorem, the theory of covering spaces, and the less well known theory of the fundamental group(oid) of an orbit space by a discontinuous group action, is best presented using the notion of groupoid rather than group as basic. This had led in the 1960s to the question of the prospective use of (strict) groupoids in higher homotopy theory. One answer is given in the book Nonabelian algebraic topology.
Properties
Equivalences of groupoids
Lemma
(automorphism group depends on basepoint only up to conjugation)
For a groupoid, let and be two objects in the same connected component (def. ). Then there is a group isomorphism
between their automorphism groups (def. ).
Proof
By assumption, there exists some morphism from to
The operation of conjugation with this morphism
is clearly a group isomorphism as required.
Lemma
(equivalences between disjoint unions of delooping groupoids)
Let and be sets of groups and consider a homomorphism (functor)
between the corresponding disjoint unions of delooping groupoids (example ).
Then the following are equivalent:
-
is an equivalence of groupoids (def. );
-
is a weak homotopy equivalence (def. ).
Proof
The implication 2) is immediate.
In the other direction, assume that is an equivalence of groupoids, and let be an inverse up to natural isomorphism. It is clear that both induces bijections on connected components. To see that both are isomorphisms of automorphisms groups, observe that the conditions for the natural isomorphisms
are in each separate delooping groupoid of the form
since there is only a single object. But this means and are group isomorphisms.
Proposition
(every groupoid is equivalent to a disjoint union of group deloopings)
Assuming the axiom of choice, then:
For any groupoid, then there exists a set of groups and an equivalence of groupoids (def. )
between and a disjoint union of delooping groupoids (example ). This is called a skeleton of .
Concretely, this exists for the set of connected components of (def. ) and for the automorphism group (def. ) of any object in the given connected component.
Proof
Using the axiom of choice we may find a set of objects of , with being in the connected component .
This choice induces a functor
which takes each object and morphism “to itself”.
Now using the axiom of choice once more, we choose in each connected component and for each object in that connected component a morphism
Using this we obtain a functor the other way around
which sends each object to its connected component, and which for pairs of objects , of is given by conjugation with the morphisms choosen above:
It is now sufficient to show that there are conjugations/natural isomorphisms
For the first this is immediate, since we even have equality
For the second we observe that choosing
yields a naturality square by the above construction:
Proposition
(weak homotopy equivalence is equivalence of groupoids)
Let be a homomorphism of groupoids.
Assuming the axiom of choice then the following are equivalent:
-
is an equivalence of groupoids (def. );
-
is a weak homotopy equivalence in that
-
for each object it induces an isomorphism of automorphism groups (def. ):
Proof
In one direction, if has an inverse up to natural isomorphism, then this induces by definition a bijection on connected components, and it induces isomorphism on homotopy groups by lemma .
In the other direction, choose equivalences to skeleta as in prop. to get a commuting diagram in the 1-category of groupoids as follows:
Here and are equivalences of groupoids by prop. . Moreover, by assumption that is a weak homotopy equivalence is the union of of deloopings of isomorphisms of groups, and hence has a strict inverse, in particular a homotopy inverse, hence is in particular an euivalence of groupoids.
In conclusion, when regarded as a diagram in the homotopy category (def. ), the top, bottom and right moprhism of the above diagram are isomorphisms. It follows that also is an isomorphism in . But this means exactly that it is a homotopy equivalence of groupoids, by def. .
Proposition
(groupoid representations are products of group representations)
Assuming the axiom of choice then the following holds:
Let be a groupoid. Then its category of groupoid representations is equivalent to the product category indexed by the set of connected components (def. ) of group representations of the automorphism group (def. ) for any object in the th connected component:
Proof
Let be the category that the representation is on. Then by definition
Consider the injection functor of the skeleton (from lemma )
By lemma the pre-composition with this constitutes a functor
and by combining lemma with lemma this is an equivalence of categories. Finally, by example the category on the right is the product of group representation categories as claimed.
As 2-coskeletal Kan complexes
Groupoids are equivalent to 1-hypergroupoids, which are in particular 2-coskeletal Kan complexes – their nerves.
The objects of the groupoids are the 0-simplices and the morphisms of the groupoid are the 1-simplices of the Kan complex. The composition operation in the grouopoid is encoded in the 2-simplices of the Kan complex
The associativity condition on the composition is exhibited by the 3-coskeleton-property of the Kan complex. This says that every simplicial 2-sphere in the Kan complex has a unique filler. With the above identification of 2-simplices with composition operations, this means that the 2 ways
of composing a sequence of three composable morphisms are equal
For handling just groupoids exclusively their description in terms of Kan complexes may be a bit of an overkill, but the advantage is that it embeds groupoids naturally in the more general context of 2-groupoids, 3-groupoids and eventually ∞-groupoids. For instance a pseudo-functor out of an ordinary groupoid into a 2-groupoid is simply a homomorphism of the corresponding Kan complexes.
The disadvantage of the simplicial approach is the difficulty of describing multiple compositions in higher dimensions, an important idea which is quite conveniently handled cubically.
Related concepts
| homotopy level | n-truncation | homotopy theory | higher category theory | higher topos theory | homotopy type theory |
|---|---|---|---|---|---|
| h-level 0 | (-2)-truncated | contractible space | (-2)-groupoid | true/unit type/contractible type | |
| h-level 1 | (-1)-truncated | contractible-if-inhabited | (-1)-groupoid/truth value | (0,1)-sheaf/ideal | mere proposition/h-proposition |
| h-level 2 | 0-truncated | homotopy 0-type | 0-groupoid/set | sheaf | h-set |
| h-level 3 | 1-truncated | homotopy 1-type | 1-groupoid/groupoid | (2,1)-sheaf/stack | h-groupoid |
| h-level 4 | 2-truncated | homotopy 2-type | 2-groupoid | (3,1)-sheaf/2-stack | h-2-groupoid |
| h-level 5 | 3-truncated | homotopy 3-type | 3-groupoid | (4,1)-sheaf/3-stack | h-3-groupoid |
| h-level | -truncated | homotopy n-type | n-groupoid | (n+1,1)-sheaf/n-stack | h--groupoid |
| h-level | untruncated | homotopy type | ∞-groupoid | (∞,1)-sheaf/∞-stack | h--groupoid |
References
Apparently the earliest occurence of the concept of groupoids (see also Brandt groupoid):
- Heinrich Brandt, Über eine Verallgemeinerung des Gruppenbegriffes, Mathematische Annalen 96 1 (1927) 360-366 [doi:10.1007/BF01209171]
Further early discussion:
-
George W. Mackey, §11 of: Ergodic theory and virtual groups, Mathematische Annalen 166 (1966) 187–207 [doi:10.1007/BF01361167]
-
Philip Higgins, Presentations of Groupoids, with Applications to Groups, Proc. Camb. Phil. Soc., 60 (1964) 7-20 [doi;10.1017/S0305004100037397]
-
Nicolas Bourbaki, Topologie Algébrique, Chapitres 1 à 4, Springer (1998, 2016) [doi:10.1007/978-3-662-49361-8, ISBN 978-3-662-49361-8]
-
Philip J. Higgins, Categories and Groupoids, Mathematical Studies 32, van Nostrand New York (1971), Reprints in Theory and Applications of Categories 7 (2005) 1-195 [tac:tr7, pdf]
A motivation and introduction of the concept of groupoid and a tour of examples (including the refinement to topological groupoids and Lie groupoids) is in
- Alan Weinstein, Groupoids: Unifying Internal and External Symmetry – A Tour through some Examples, Notices of the AMS 43 7 (1996) [pdf, pdf]
Further exposition:
-
Ronnie Brown, From groups to groupoids: A brief survey, at Groupoids in Mathematics, Bulletin of the London Mathematical Society 19 2 (1987) 113-134 [doi:10.1112/blms/19.2.113, pdf]
-
Alberto Santini, Topological groupoids (2011) [pdf, pdf]
(about groupoids in topology, notably fundamental groupoids – not about topological groupoids)
With an eye towards homotopy theory:
- Birgit Richter, Section 1.2 of: From categories to homotopy theory, Cambridge Studies in Advanced Mathematics 188, Cambridge University Press 2020 (doi:10.1017/9781108855891, book webpage, pdf)
See also:
-
Ronnie Brown, Topology and groupoids, Booksurge, 2006. (web)
-
Rade T. Živaljević, Groupoids in combinatorics—applications of a theory of local symmetries, Algebraic and geometric combinatorics, 305–324, Contemp. Math., 423, Amer. Math. Soc., Providence, RI, 2006.
Presenting a pretorsion theory on Cat whose torsion(-free) objects are the groupoids (skeletal categories, respectively), hence whose “trivial objects” are the skeletal groupoids:
- Francis Borceux, Federico Campanini, Marino Gran, Walter Tholen, Groupoids and skeletal categories form a pretorsion theory in [arXiv:2207.08487]
Last revised on November 18, 2023 at 05:18:07. See the history of this page for a list of all contributions to it.