nLab
representable functor

Idea

For $C$ is a locally small category, a presheaf on $C$ or equivalently a functor

$$F:C^{\mathrm{op}}\to \mathrm{Set}$$F: C^{op} \to Set

on the opposite category of $C$ with values in Set is representable if it is naturally isomorphic to a hom-functor $h_X:={\mathrm{hom}}_C(-,X):C^{\mathrm{op}}\to \mathrm{Set}$, which sends an object $U\in C$ to the hom-set ${\mathrm{Hom}}_C(U,X)$ in $C$

and which sends a morphism $\alpha :U\prime \to U$ in $C$ to the function which sends each morphism $U\to X$ to the composite $U\prime \stackrel{\alpha }{\to }U\to X$

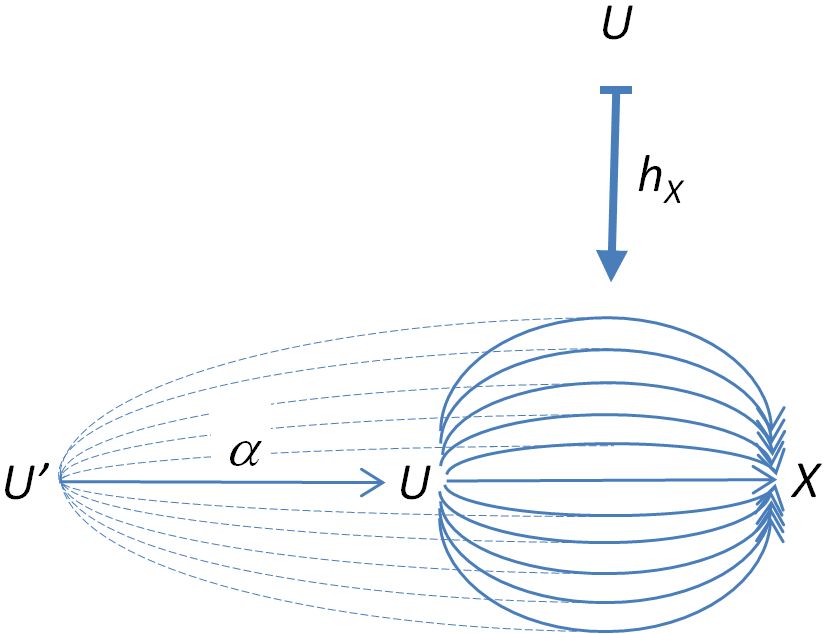
If we picture ${\mathrm{Hom}}_C(U,X)$ as strands of morphisms as above, then the morphism $\alpha :U\prime \to U$ serves to “comb” the strands back from ${\mathrm{Hom}}_C(U,X)$ to ${\mathrm{Hom}}_C(U\prime ,X)$, i.e.

$$h_X\alpha :{\mathrm{Hom}}_C(U,X)\to {\mathrm{Hom}}_C(U\prime ,X).$$h_X\alpha: Hom_C(U,X)\to Hom_C(U',X).

The object $X$ is determined uniquely up to isomorphism in $C$, and is called a representing object for $F$.

Representability is one of the most fundamental concepts of category theory, with close ties to the notion of adjoint functor and to the Yoneda lemma. It is the crucial concept underlying the idea of universal property; thus for example crucial concepts such as “limit”, “colimit”, “exponential object”, “Kan extension” and so on are naturally expressed in terms of representing objects. The concept permeates much of algebraic geometry and algebraic topology.

Definition

In ordinary category theory

For a functor $F:C^{\mathrm{op}}\to \mathrm{Set}$ (also called a presheaf on $C$), a representation of $F$ is a specified natural isomorphism

$$\theta :{\mathrm{hom}}_C(-,c)\stackrel{\sim }{\to }F$$\theta: \hom_C(-, c) \stackrel{\sim}{\to} F

By the Yoneda lemma, any such transformation $\theta$ (isomorphism or not) is uniquely determined by an element $\xi \in F(c)$. As above, the object $c$ is called a representing object (or often, universal object) for $F$, and the element $\xi$ is called a universal element for $F$. Again, it follows from the Yoneda lemma that the pair $(c,\xi )$ is determined uniquely up to unique isomorphism.

Following the proof of the Yoneda lemma, representability means precisely this: given any object $x$ of $C$ and any element $\alpha \in F(x)$, there exists a unique morphism $f:x\to c$ such that the function $F(f)$ carries the universal element $\xi \in F(c)$ to $\alpha \in F(x)$. Such a dry formulation fails to convey the remarkable power of this concept, which can really only be appreciated through the myriad examples which illustrate it.

In enriched category theory

The above definition generalizes straightforwardly to enriched category theory.

Let $V$ be a closed monoidal category and $C$ a $V$-enriched category.

Then for every object $c\in C$ there is a $V$-enriched functor

$$C(c,-):C\to V$$C(c,-) : C \to V

from $C$ to $V$ regarded canonically as a $V$-enriched category.

This is defined

• on objects by $C(c,-):d\mapsto C(c,d)\in V$

• on morphisms between $d$ and $d\prime$ by

$$C(c,-{)}_{d,d\prime }:C(d,d\prime )\to [C(c,d),C(c,d\prime )],$$C(c,-)_{d,d'} : C(d,d') \to [C(c,d), C(c,d')] \,,

being the adjunct of the composition morphism

$${\circ }_{c,d,d\prime }:C(d,d\prime )\otimes C(c,d)\to C(c,d\prime ).$$\circ_{c,d,d'} : C(d,d') \otimes C(c,d) \to C(c,d') \,.

A $V$-enriched functor $F:C\to V$ is representable if there is $c\in C$ and a $V$-enriched natural transformation $\eta :F\to C(c,-)$.

If $V$ is symmetric monoidal one can form the opposite category $C^{\mathrm{op}}$ and have the analogous definition for representable functors $F:C^{\mathrm{op}}\to V$.

In higher category theory

The notion of representable functors has its straightforward analogs also in higher category theory.

• For 2-category theory see … .

• For (∞,1)-category theory theory see (∞,1)-presheaf

Examples

The central point about examples of representable functors is:

Representable functors are ubiquitous .

To a fair extent, category theory is all about representable functors and the other universal constructions: Kan extensions, adjoint functors, limits, which are all special cases of representable functors – and representable functors are special cases of these.

Listing examples of representable functors in category theory is much like listing examples of integrals in analysis: one can and does fill books with these. (In fact, that analogy has more to it than meets the casual eye: see coend for more).

Keeping that in mind, we do list some special cases and special classes of examples that are useful to know. But any list is necessarily wildly incomplete.

Limits

If $F:J\to C$ is a diagram in $C$, we can construct a diagram ${\mathrm{hom}}_C(-,F)$ in the functor category ${\mathrm{Set}}^{C^{\mathrm{op}}}$ as the composite of $F$ with the curried hom-functor $C\to {Set}^{C^{\mathrm{op}}}$ (the Yoneda embedding). The object-wise limit of this diagram in Set, that is, the functor $C^{\mathrm{op}}\to Set$ sending on object $x$ to the set which is the limit of the diagram ${\mathrm{hom}}_C(x,F):J\to Set$, is representable iff the diagram $F$ has a limit in $C$; in fact, a representing object for that limit functor is exactly $\lim F$, and we obtain a natural isomorphism

$$\lim {\mathrm{hom}}_C(-,F)\cong {\mathrm{hom}}_C(-,\lim F).$$\lim\hom_C(-,F)\cong\hom_C(-,\lim F).

Products

For an example in the case of the product, let $c,d$ be objects of $C$, and consider the presheaf given by a product of hom-functors

$${\mathrm{hom}}_C(-,c)\times {\mathrm{hom}}_C(-,d):C^{\mathrm{op}}\to \mathrm{Set};$$\hom_C(-, c) \times \hom_C(-, d): C^{op} \to Set;

that is, the functor which takes an object $x$ of $C$ to the set ${\mathrm{hom}}_C(x,c)\times {\mathrm{hom}}_C(x,d)$. A product $c\times d$ is precisely a representing or universal object for this presheaf, where the universal element is precisely the pair of projection maps

$$({\pi }_c,{\pi }_d)\in \mathrm{hom}(c\times d,c)\times \mathrm{hom}(c\times d,d)$$(\pi_c, \pi_d) \in \hom(c \times d, c) \times \hom(c \times d, d)

We leave it to the reader to check that the representability here means precisely that given a pair of maps

$$(f,g)\in \mathrm{hom}(x,c)\times \mathrm{hom}(x,d)$$(f, g) \in \hom(x, c) \times \hom(x, d)

there exists a unique element in $\mathrm{hom}(x,c\times d)$, denoted $⟨f,g⟩$, such that

$${\pi }_c⟨f,g⟩=f{\pi }_d⟨f,g⟩=g.$$\pi_c \langle f, g \rangle = f \qquad \pi_d \langle f, g \rangle = g.

Weighted limits

The above example has an important straightforward generalization.

Noticing that the limit over the functor $H:J\to \mathrm{Set}$ is just the collection of cones over $H$ whose tip is the point

$$\lim H=[J,\mathrm{Set}](\Delta \mathrm{pt},H)$$lim H = [J,Set](\Delta pt, H)

the above expression $\lim {\mathrm{hom}}_C(-,F)$ can be rewritten equivalently as $[J,\mathrm{Set}](\Delta \mathrm{pt},C(-,F(-)))$. Replacing in this expression the constant terminal functor $\Delta \mathrm{pt}:J\to \mathrm{Set}$ by any other functor leads to the notion of weighted limit, as described there.

Exponential objects

Suppose $C$ is a category which admits finite products; given objects $c,d$, consider the presheaf

$${\mathrm{hom}}_C(-\times c,d):C^{\mathrm{op}}\to \mathrm{Set}.$$\hom_C(- \times c, d): C^{op} \to Set.

A representing or universal object for this presheaf is an exponential object $d^c$; the universal element

$$e\in {\mathrm{hom}}_C(d^c\times c,d)$$e \in \hom_C(d^c \times c, d)

is a morphism called the evaluation map $\mathrm{eval}:d^c\times c\to d$.

Classifying bundles

Consider a category $\mathrm{Top}$ of ‘nice’ spaces (just to fix the discussion, let’s say paracompact spaces, although this is a technical point), and a topological group $G$ therein, i.e., a group internal to $\mathrm{Top}$. There is a presheaf

$$GBund:{\mathrm{Top}}^{\mathrm{op}}\to \mathrm{Set}$$G\Bund: Top^{op} \to Set

which assigns to each space $X$ the set of isomorphism classes of $G$-bundles over $X$, and assigns to each continuous map $f:X\to Y$ the function

$$GBund(f):GBund(Y)\to GBund(X)$$G\Bund(f): G\Bund(Y) \to G\Bund(X)

which carries a (class of a) $G$-bundle $E\to Y$ to the (class of the) pullback bundle $f^{*}E\to X$. It is well-known that the pullback construction is invariant with respect to homotopic deformations; that is, this presheaf descends to a functor on the homotopy category,

$$GBund:{\mathrm{Ho}}_{\mathrm{Top}}^{\mathrm{op}}\to \mathrm{Set}.$$G\Bund: Ho_{Top}^{op} \to Set.

A classifying space $ℬG$ is precisely a representing object for this functor; the universal element is the (isomorphism class of the) classifying $G$-bundle $[\pi :ℰG\to ℬG]$.

These general considerations are quite commonplace in algebraic topology, where they crop up for example in the connection between generalized cohomology theories and spectra; cf. Brown’s representability theorem.

Related concepts

• Yoneda lemma

• classifying space, classifying stack, moduli space, moduli stack, derived moduli space

• classifying morphism

• representable morphism of stacks

References

A discussion of representable functors in the context of enriched category theory is in section 1.6 and section 1.10 of

• Max Kelly, Basic concepts of enriched category theory (pdf)

A query discussion on differences between representable functor and representation of a functor is archived here.