nLab permutation representation
Context
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
-
Be?linson-Bernstein localization?
Contents
Definition
For a group (tyically a finite group), consider a G-set , hence a set (typically a finite set), equipped with an action of
Equivalently this is a group homomorphism
from to the group of permutations of elements of . As such it is a representation of “by permutations”.
Specifically, if is a finite set and an isomorphism is understood, it is equivalently a group homomorphism
to the symmetric group on elements.
For any field (or, more generally, any commutative ring, but one mostly considers fields) this -action may be linearized to a -linear representation of in an evident way:
Definition
(linear permutation representation)
The linear permutation representation of a G-set is the following -linear representation of :
-
The underlying -vector space is the freely spanned vector space , whose elements (vectors) are the formal linear combinations
of elements of with coefficients in , hence is the -vector space for which is a canonical linear basis.
-
The linear -action
is given on linear basis-elements by , which uniquely defines it by linearity to act on a general vector as
This concept immediately generalizes to groupoid representations and so forth, see also at infinity-action the section Examples – Discrete group actions on sets.
Properties
Functoriality
Proposition
(functoriality of linear permutation representations)
The construction of linear permutation representations (Def. ) evidently extends to a functor from the category of G-sets to the category of linear representations
Both of these categories are rig categories with respect to disjoint union and Cartesian product on the left, and direct sum and tensor product of representations on the right.
The functor is canonically a homomorphism of rig-categories in that in that it is canonically a strong monoidal functor for both “addition” and “multiplication” monoidal structures:
Comparison from Burnside- to representation ring
Let be a finite group and assume all G-sets in the following to be finite sets and all linear representations to be finite dimensional.
Consider
-
the Burnside ring , which is the Grothendieck ring of the rig-category of finite G-sets;
-
the representation ring , which is the Grothendieck ring of the rig category of finite-dimensional linear G-representations.
Definition
(permutation representations make ring homomorphism from Burnside ring to representation ring)
Since forming -linear permutation representations (Def. ) is a rig-functor (Prop. ), under passing to Grothendieck rings it induces a ring homomorphism
from the Burnside ring of to its representation ring.
This homomorphism is traditionally denoted , as shown.
Its kernel is known as the Brauer relations (e.g. Bartel-Dokchitser 11).
Remark
(virtual linear permutation representations)
The image of the comparison morphism (Def. ) may be called the virtual linear permutation representations.
Remark
(virtual permutation representations from equivariant stable cohomotopy into equivariant K-theory)
Under the identitification
-
of the Burnside ring with the equivariant stable cohomotopy of the point
(see there)
-
of the representation ring with the equivariant K-theory of the point
(see there)
the ring homomorphism of Def. should be image under forming equivariant cohomology of the point of the initial morphism of E-infinity ring spectra
from the sphere spectrum to KU.
Noticing that we may regard stable cohomotopy/the sphere spectrum as being the algebraic K-theory of the “field with one element” (see there)
we may regard this as extension of scalars along followed by the comparison map between algebraic and topological K-theory:
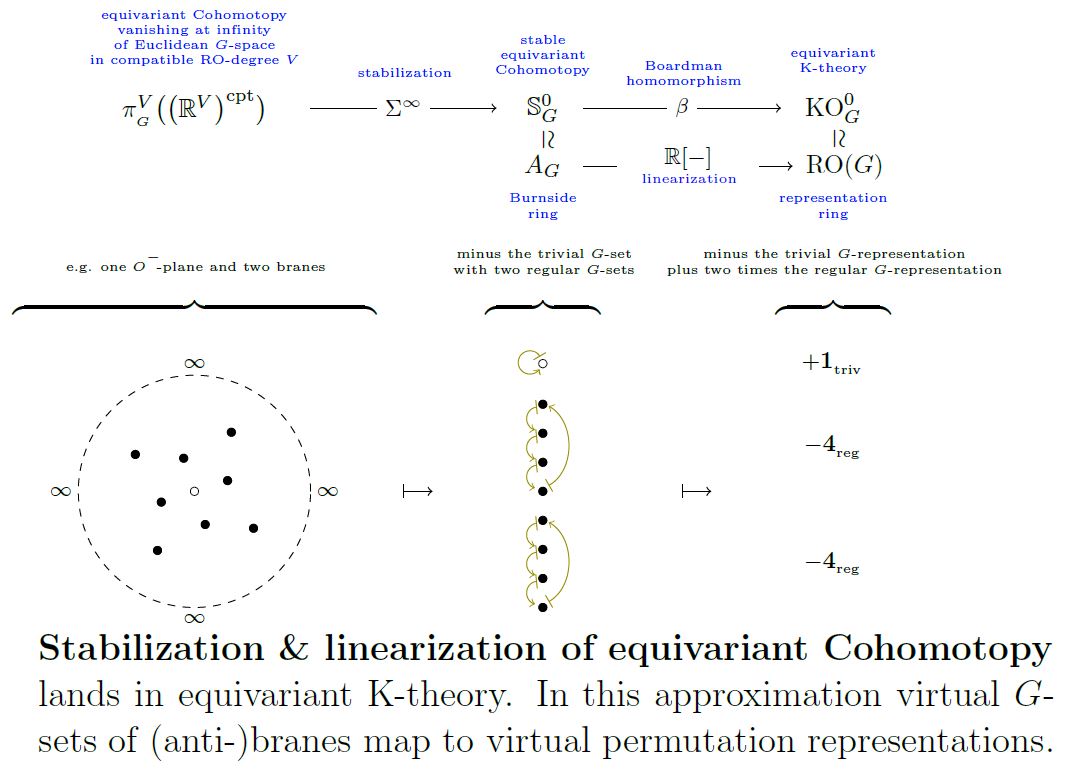
graphics grabbed from SS19
See also at equivariant Hopf degree theorem.
Characters
The characters of permutation representations are the Burnside marks of the underlying G-sets:
Proposition
(mark homomorphism on cyclic groups agrees with characters of corresponding permutation representations)
For a finite G-set, for any field and the corresponding permutation representation, the character of the permutation representation at any equals the Burnside marks (Def. ) of under the cyclic group generated by :
Hence the mark homomorphism (Def. ) of -sets restricted to cyclic subgroups coincides with the characters of their permutation representations.
This statement immediately generalizes from plain representations to virtual representations, hence to the Burnside ring.
(e.g. tom Dieck 09, (2.15))
Proof
By definition of character of a linear representation, we have that
is the trace of the linear endomorphism of the given permutation representation.
Now the canonical -linear basis for is of course the set itself, and so
Here in the first step we spelled out the definition of trace in the canonical basis, and in the second step we observed that the fixed point set of a cyclic group equals that of any one of its generating elements.
Examples
Basic examples
Example
For a group, write, for emphasis, for its underlying set. Let
be the canonical action of on itself, by left multiplication in the group. The corresponding linear permutation representation (Def. ) is called the regular representation of .
Example
(induced representation of the trivial representation)
Let be a finite group and a subgroup-inclusion. Then the induced representation in Rep(G) of the trivial representation is the permutation representation of the coset G-set :
This follows directly as a special case of the general formula for induced representations of finite groups (this Example).
See at induced representation of the trivial representation for more.
Virtual permutation representations
We discuss here examples of the operation of forming virtual linear permutation representations (Remark ), regarded as the canonical ring homomorphism
For emphasis, notice that among plain linear representations the linear permutation representations generally form but a tiny sub-class, i.e. generically a linear representation is not a linear permutation representation. But this statement may change radically as we pass to virtual representations:
If the ring homomorphism (Def. ) is a surjective function, this means that in fact all virtual linear -representation are virtual linear permutation representations. This is not the case for all groups, but it is the case for large classes of groups! This is the content of Prop. below.
Notice that when this is the case, it means that the representation theory of the given group is, in a precise sense, purely combinatorial, or equivalently, in view of (1), that it is fully determined over the absolute ground field .
Proposition
(virtual linear reps from virtual permutation reps)
For ground field the rational numbers, the comparison morphism
from Def. , which sends virtual G-sets to their permutation rep virtual linear G-representations,
-
is surjective for among one of the following classes of finite groups (not mutually exclusive)
-
is not surjective for (direct product of cyclic group of order 3 with quaternion group or order 8);
-
is injective precisely for cyclic groups,
-
hence is an isomorphism precisely for cyclic groups.
Proof
Isomorphy for the case of cyclic groups is spelled out in tom Dieck 09, Example (4.4.4).
Surjectivity for the case of symmetric groups follows from the theory of Young diagrams (Dress 86, section 3), see also Example below for further pointers.
The proof of surjectivity for p-primary groups is due to Segal 72. (As Segal remarks on his first page, it may also be deduced from Feit 67 (14.3). See also Ritter 72.) The proof is recalled as tom Dieck 79, Theorem 4.4.1.
Surjectivity for binary dihedral groups for (at least) , the binary tetrahedral group, binary octahedral group, binary icosahedral group and the general linear group is checked by computer experiment in Burton-Sati-Schreiber 18.
The non-surjectivity for was remarked in Serre 77, p. 104.
To see that injectivity holds at most for cyclic groups, notice that over we have that
-
the number of isomorphism classes of irreducible representations of equals the number of conjugacy classes of cyclic subgroups;
-
the number of isomorphism classes of indecomposable (transitive) G-sets (i.e. -orbit types) is the number of conjugacy classes of all subgroups.
This means that for not a cyclic group we have that the free abelian group has more generators than , so that cannot be injective.
A more general analysis of the cokernel of is due to Berz 94, reviewed and expanded on in Hambleton-Taylor 99. See also Bartel-Dokchitser 14, p. 1.
Example
(virtual permutation representations of the group of order 2
Let be the cyclic group of order 2.
It has two conjugacy classes of subgroups,
-
the group itself,
-
the trivial group;
and hence two isomorphism classes of transitive G-sets
-
the point with the trivial action,
-
the group itself, with the regular action.
The corresponding linear permutation representations (Def. ) are
-
,
the 1-dimensional trivial representation;
-
,
the direct sum of the 1d trivial representation with the alternating representation.
To see the second item, observe that the non-trivial element is represented on by the permutation matrix
which is diagonalizable over with eigenvectors
-
of eigenvalue , spanning the trivial representation of dimension 1;
-
of eigenvalue , spanning the alternating representation of dimension 1.
Hence, the abelian group underlying the representation ring may be identified with the linear span
and the comparison morphism from the Burnside ring (Def. ) is
which is manifestly an isomorphism, in accord with Prop. .
Example
(virtual permutation representations of symmetric groups)
For a symmetric group on elements, the comparison morphism from the Burnside ring to the representation ring (Def. )
is a surjective map over but also over and .
The special case of is made explicit for in Montaldi, bottom of this page, and for at Categorified Gram-Schmidt process.
Related concepts
References
Textbook accounts and lecture notes include
-
Charles Curtis, Irving Reiner, from p. 43 on in Representation theory of finite groups and associative algebras, AMS 1962
-
Walter Feit, Characters of Finite Groups, W. A. Benjamin New York, 1967
-
Tammo tom Dieck, Section 4 of Transformation Groups and Representation Theory, Lecture Notes in Mathematics 766, Springer 1979 (doi:10.1007/BFb0085965)
-
Tammo tom Dieck, section 1.2 of Representation theory, 2009 (pdf)
Original articles include
-
D. L. Johnson, Minimal Permutation Representations of Finite Groups, American Journal of Mathematics Vol. 93, No. 4 (Oct., 1971), pp. 857-866 (jstor:2373739)
-
J. Ritter, Ein Induktionssatz fuer rationale Charaktere von nilpotenten Gruppen, J. Reine Angew. Math. 254 (1972), 133–151
-
Graeme Segal, Permutation representations of finite -groups, Quart. J. Math. Oxford (2) 23 (1972), 375–381 (doi:10.1093/qmath/23.4.375)
-
Jean-Pierre Serre, Linear Representations of Finite Groups, Graduate Texts in Math., vol. 42, Springer–Verlag, New York, 1977
-
Andreas Dress, Congruence relations characterizing the representation ring of the symmetric group, Journal of Algebra 101, 350-364 (1986) (pdf, pdf)
-
G. Berz, Permutationsbasen fuer endliche Gruppen, Ph.D. thesis, Augsburg, 1994 (Zbl0924.20003)
-
I. Hambleton, L. R. Taylor, Rational permutation modules for finite groups, Math. Z. 231 (1999), 707–726 (pdf)
-
Alex Bartel, Tim Dokchitser, Brauer relations in finite groups, J. Eur. Math. Soc. 17 (2015), 2473-2512 (arXiv:1103.2047)
-
Alex Bartel, Tim Dokchitser, Rational representations and permutation representations of finite groups, Math. Ann. 364 no. 1 (2016), 539-558 (arXiv:1405.6616)
-
Vladimir V. Kornyak, An Algorithm to Decompose Permutation Representations of Finite Groups: Polynomial Algebra Approach (arXiv:1801.09786)
-
Simon Burton, Hisham Sati, Urs Schreiber, Lift of fractional D-brane charge to equivariant Cohomotopy theory (arXiv:1812.09679, Python code)
See also
Last revised on June 15, 2021 at 05:48:13. See the history of this page for a list of all contributions to it.