nLab coset
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Idea
Given a group and a subgroup , then their coset object is the quotient , hence the set of equivalence classes of elements of where two are regarded as equivalent if they differ by right multiplication with an element in .
If is a topological group, then the quotient is a topological space and usually called the coset space. This is in particular a homogeneous space, see there for more.
Definition
Internal to a general category
In a category , for a group object and a subgroup object, the left/right object of cosets is the object of orbits of under left/right multiplication by .
Explicitly, the left coset space coequalizes the parallel morphisms
where is (the inclusion composed with) the group multiplication.
Simiarly, the right coset space coequalizes the parallel morphisms
Internal to
Specializing the above definition to the case where is the well-pointed topos , given an element of , its orbit is an element of and is called a left coset.
Using comprehension, we can write
Similarly there is a coset on the right .
For Lie groups and Klein geometry
If is an inclusion of Lie groups then the quotient is also called a Klein geometry.
For -groups
More generally, given an (∞,1)-topos and a homomorphism of ∞-group objects , hence equivalently a morphism of their deloopings , then the homotopy quotient is given by the homotopy fiber of this map
See at ∞-action for more on this definition. See at higher Klein geometry and higher Cartan geometry for the corresponding concepts of higher geometry.
Properties
For normal subgroups
The coset inherits the structure of a group if is a normal subgroup.
Unless is abelian, considering both left and right coset spaces provide different information.
Topology of the quotient map
Proposition
For a smooth manifold and a compact Lie group equipped with a free smooth action on , then the quotient projection
is a -principal bundle (hence in particular a Serre fibration).
This is originally due to (Gleason 50). See e.g. (Cohen, theorem 1.3)
Corollary
For a Lie group and a compact subgroup, then the coset quotient projection
is an -principal bundle (hence in particular a Serre fibration).
This is originally due to (Samelson 41).
Proposition
For a compact Lie group and closed subgroups, then the projection map
is a locally trivial -fiber bundle (hence in particular a Serre fibration).
Proof
Observe that the projection map in question is equivalently
(where on the left we form the Cartesian product and then divide out the diagonal action by ). This exhibits it as the -fiber bundle associated to the -principal bundle of corollary .
Proposition
(coset space coprojections with local sections)
Let be a topological group and a subgroup.
Sufficient conditions for the coset space coprojection to admit local sections, in that there is an open cover and a continuous section of the pullback of to the cover,
include the following:
-
is any topological group
and is a compact Lie group
(in particular for a closed subgroup if itself is a compact Lie group, since closed subspaces of compact Hausdorff spaces are equivalently compact subspaces).
or:
-
The underlying topological space of is
(e.g. if is a Lie group)
and is a closed subgroup.
As a homotopy fiber
Remark
In geometric homotopy theory (in an (∞,1)-topos), for any homomorphisms of ∞-group objects, then the natural projection , generally realizes as an -principal ∞-bundle over . This is exhibited by a homotopy pullback of the form
where is the delooping groupoid of . This also equivalently exhibits the ∞-action of on (see there for more).
By the reverse pasting law for homotopy pullbacks (here, using that is an effective epimorphism by definition of delooping) then we get the homotopy pullback
which exhibits the coset as the homotopy fiber of .
See also SS21, Ex. 3.2.35.
Examples
-Spheres
Example
The n-spheres are coset spaces of orthogonal groups:
The odd-dimensional spheres are also coset spaces of unitary groups:
Proof
Regarding the first statement:
Fix a unit vector in . Then its orbit under the defining -action on is clearly the canonical embedding . But precisely the subgroup of that consists of rotations around the axis formed by that unit vector stabilizes it, and that subgroup is isomorphic to , hence .
The second statement follows by the same kind of reasoning:
Clearly acts transitively on the unit sphere in . It remains to see that its stabilizer subgroup of any point on this sphere is . If we take the point with coordinates and regard elements of as matrices, then the stabilizer subgroup consists of matrices of the block diagonal form
where .
There are also various exceptional realizations of spheres as coset spaces. For instance:
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G2 is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G2/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
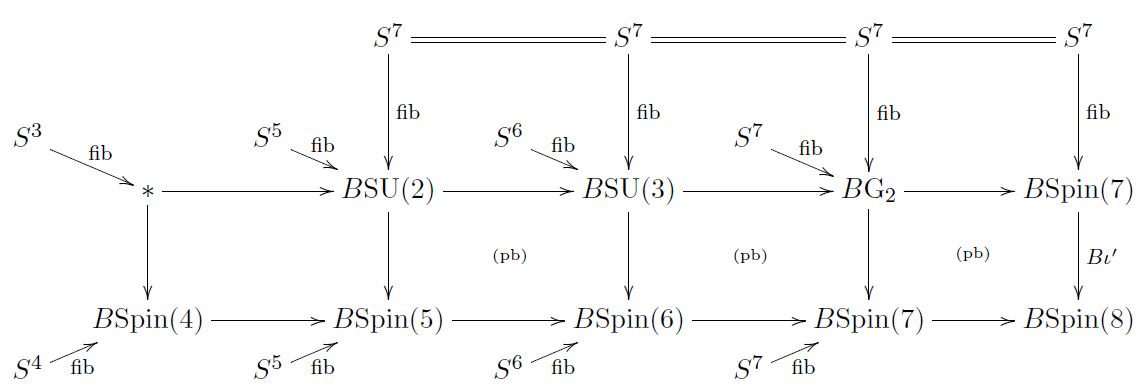
(from FSS 19, 3.4)
Sequences of coset spaces
Consider two consecutive group inclusions with their induced coset quotient projections
When is a Serre fibration, for instance in the situation of prop. (so that this is indeed a homotopy fiber sequence with respect to the classical model structure on topological spaces) then it induces the corresponding long exact sequence of homotopy groups
Example
Consider a sequence of inclusions of orthogonal groups of the form
Then by example we have that is the n-sphere and by corollary the quotient map is a Serre fibration. Hence there is a long exact sequence of homotopy groups of the form
Now for then and hence in this range we have isomorphisms
Related concepts
References
-
Hans Samelson, Beiträge zur Topologie der Gruppenmannigfaltigkeiten, Ann. of Math. 2, 42, (1941), 1091 - 1137. (jstor:1970463, doi:10.2307/1970463)
-
Andrew Gleason, Spaces with a compact Lie group of transformations, Proc. of A.M.S 1, (1950), 35 - 43 (jstor:2032430, doi:10.2307/2032430)
-
Norman Steenrod, Section I.7 of: The topology of fibre bundles, Princeton Mathematical Series 14, Princeton Univ. Press, 1951.
-
Paul Mostert, Local Cross Sections in Locally Compact Groups, Proceedings of the American Mathematical Society, Vol. 4, No. 4 (Aug., 1953), pp.645-649 (jstor:2032540, doi:10.2307/2032540)
-
Glen Bredon, Section I.4 of: Introduction to compact transformation groups, Academic Press 1972 (ISBN 9780080873596, pdf)
-
R. Cohen, Topology of fiber bundles, Lecture notes (pdf)
On coset spaces with the same rational cohomology as a product of n-spheres:
- Linus Kramer, Homogeneous Spaces, Tits Buildings, and Isoparametric Hypersurface, Memoirs of the American Mathematical Society number 752 (arXiv:math/0109133, doi:10.1090/memo/0752, GoogleBooks)
Discussion in -topos theory:
- Hisham Sati, Urs Schreiber, Ex. 3.2.35 (p. 104) of: Equivariant principal infinity-bundles [arXiv:2112.13654]
Last revised on December 13, 2023 at 17:57:17. See the history of this page for a list of all contributions to it.