nLab F-theory

Idea

F-theory is a toolbox for describing type IIB string theory backgrounds – including non-perturbative effects induced from the presence of D7-branes and (p,q)-strings – in terms of complex elliptic fibrations whose fiber modulus $\tau$ encodes the axio-dilaton (the string coupling constant and the degree-0 RR-field) transforming under the $SL(2, \mathbb{Z})$ S-duality/U-duality group. See also at duality in string theory.

More technically, F-theory is what results when KK-compactifying M-theory on an elliptic fibration (which yields type IIA superstring theory compactified on a circle-fiber bundle) followed by T-duality with respect to one of the two cycles of the elliptic fiber. The result is (uncompactified) type IIB superstring theory with axio-dilaton given by the moduli of the original elliptic fibration, see below.

Or rather, this is type IIB string theory with some non-perturbative effects included, reducing to perturbative string theory in the Sen limit. With a full description of M-theory available also F-theory should be a full non-perturbative description of type IIB string theory, but absent that it is some kind of approximation. For instance while the modular structure group of the elliptic fibration in principle encodes (necessarily non-perturbative) S-duality effects, it is presently not actually known in full detail how this affects the full theory, notably the proper charge quantization law of the 3-form fluxes, see at S-duality – Cohomological nature of the fields under S-duality for more on that.

Properties

Relation to M-theory

The duality between M-theory and F-theory:

The following line of argument shows why first compactifying M-theory on a torus $S_1^A \times S_1^B$ to get type IIA on a circle and then T-dualizing that circle to get type IIB indeed only depends on the shape $\frac{R_A}{R_B}$ of the torus, but not on its other geometry.

By the dualities in string theory, 10-dimensional type II string theory is supposed to be obtained from the UV-completion of 11-dimensional supergravity by first dimensionally reducing over a circle $S^1_A$ – to obtain type IIA supergravity – and then applying T-duality along another circle $S^1_B$ to obtain type IIB supergravity.

To obtain type IIB sugra in noncompact 10 dimensions this way, also $S^1_B$ is to be compactified (since T-duality sends the radius $r_A$ of $S^1_A$ to the inverse radius $r_B = \ell_s^2 / R_A$ of $S^1_B$). Therefore type IIB sugra in $d = 10$ is obtained from 11d sugra compactified on the torus $S^1_A \times S^1_B$. More generally, this torus may be taken to be an elliptic curve and this may vary over the 9d base space as an elliptic fibration.

Applying T-duality to one of the compact direction yields a 10-dimensional theory which may now be thought of as encoded by a 12-dimensional elliptic fibration. This 12d elliptic fibration encoding a 10d type II supergravity vacuum is the input data that F-theory is concerned with.

A schematic depiction of this story is the following:

M-theory in $d = 11$		F-theory in $d = 12$
$\downarrow$ KK-reduction along elliptic fibration		$\downarrow$ axio-dilaton is modulus of elliptic fibration
IIA string theory in $d = 9$	$\leftarrow$T-duality$\rightarrow$	IIB string theory in $d = 10$

In the simple case where the elliptic fiber is indeed just $S^1_A \times S^1_B$, the imaginary part of its complex modulus is

$$Im(\tau) = \frac{R_A}{R_B} \,.$$

By following through the above diagram, one finds how this determines the coupling constant in the type II string theory:

First, the KK-compactification of M-theory on $S^1_A$ yields a type IIA string coupling

$$g_{IIA} = \frac{R_A}{\ell_s} \,.$$

Then the T-duality operation along $S^1_B$ divides this by $R_B$:

$$\begin{aligned} g_{IIB} & = g_{IIA} \frac{\ell_s}{R_B} \\ & = \frac{R_A}{R_B} \\ & = Im(\tau) \end{aligned} \,.$$

Relation to M-theory on $G_2$-manifolds

In order to get minimal N=1 d=4 supergravity after KK-compactification, one needs M-theory on G₂-manifolds and F-theory on CY4-manifolds.

Discussion of the relation between then G₂-manifold fibers for M-theory on G₂-manifolds and the corresponding Calabi-Yau 4-manifold fibers in F-theory includes (Gukov-Yau-Zaslow 02, Belhaj 02).

Relation to heterotic M-theory on ADE-singularities

Relation to heterotic M-theory on ADE-singularities:

• Monika Marquart, Daniel Waldram, F-theory duals of M-theory on $S^1/\mathbb{Z}_2 \times T^4 / \mathbb{Z}_N$ (arXiv:hep-th/0204228)

• Christoph Lüdeling, Fabian Ruehle, F-theory duals of singular heterotic K3 models, Phys. Rev. D 91, 026010 (2015) (arXiv:1405.2928)

Relation to orientifold type II backgrounds

The general vacuum of type II superstring theory (including type I superstring theory) is an orientifold.

The target space data of an orientifold is a $\mathbb{Z}_2$-principal bundle/local system, possibly singular (hence possibly on a smooth stack). On the other hand, the non-singular part of the elliptic fibration that defines the F-theory is a $SL_2(\mathbb{Z})$-local system (being the “homological invariant” of the elliptic fibration).

An argument due to (Sen 96, Sen 97a) says that the F-theory data does induce the orientifold data along the subgroup inclusion $\mathbb{Z}_2 \hookrightarrow SL_2(\mathbb{Z})$. See at Sen limit.

The degeneration locus of the elliptic fibration – where the discriminant $\Delta$ vanishes and its fibers are the nodal curve – is interpreted as that of D7-branes and O7-planes (Sen 97a, (3), Blumenhagen 10, (11)), exhibiting gauge enhancement Sen 97b see below.

Reasoning like this might suggest that in generalization to how type II orientifolds involve $\mathbb{Z}_2$-equivariant K-theory (namely KR-theory), so F-theory should involve $SL_2(\mathbb{Z})$-equivariant elliptic cohomology. This was conjectured in (Kriz-Sati 05, p. 3, p.17, 18). For more on this see at modular equivariant elliptic cohomology.

Relation to heterotic string theory

The duality between F-theory and heterotic string theory:A subclass of K3 manifolds elliptically fibered.

F-theory on an elliptically fibered K3 is supposed to be equivalent to heterotic string theory compactified on a 2-torus. An early argument for this is due to (Sen 96).

More generally, heterotic string theory on an elliptically fibered Calabi-Yau $Z \to B$ of complex dimension $(n-1)$ is supposed to be equivalent $F$-theory on an $n$-dimensional $X\to B$ with elliptic K3-fibers.

A detailed discussion of the equivalence of the respective moduli spaces is originally due to (Friedman-Morgan-Witten 97). A review of this is in (Donagi 98).

Singular locus of the elliptic fibration and D7-branes

In passing from M-theory to type IIA string theory, the locus of any Kaluza-Klein monopole in 11d becomes the locus of D6-branes in 10d. The locus of the Kaluza-Klein monopole in turn (as discussed there) is the locus where the $S^1_A$-circle fibration degenerates. Hence in F-theory this is the locus where the fiber of the $S^1_A \times S^1_B$-elliptic fibration degenerates to the nodal curve. Since the T-dual of D6-branes are D7-branes, it follows that D7-branes in F-theory “are” the singular locus of the elliptic fibration.

Now an elliptically fibered complex K3-surface

$$\array{ T &\longrightarrow& K3 \\ && \downarrow \\ && \mathbb{C}\mathbb{P}^1 }$$

may be parameterized via the Weierstrass elliptic function as the solution locus of the equation

$$y^2 = x^3 + f(z) x + g(z)$$

for $x,y,z \in \mathbb{C}\mathbb{P}^1$, with $f$ a polynomial of degree 8 and $g$ of degree twelve. The j-invariant of the complex elliptic curve which this parameterizes for given $z$ is

$$j(\tau(z)) = \frac{4 (24 f)^3}{27 g^2 + 4 f^3} \,.$$

The poles $j\to \infty$ of the j-invariant correspond to the nodal curve, and hence it is at these poles that the D7-branes are located.

from SS21

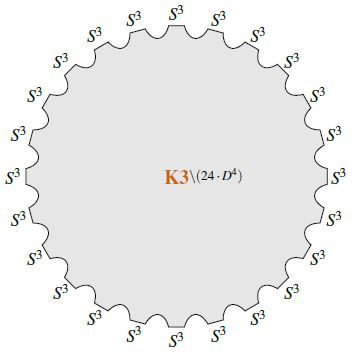
Since the order of the poles is 24 (the polynomial degree of the discriminant $\Delta = 27 g^2 + 4 f^3$, see at elliptically fibered K3-surface – singular points) there are necessarily 24 D7-branes (Sen 96, page 5, Sen 97b, see also Morrison 04, sections 8 and 17, Denef 08, around (3.41), Douglas-Park-Schnell 14).

Under T-duality this translates to 24 D6-branes in type IIA string theory on K3 (Vafa 96, Footnote 2 on p. 6).

Notice that the net charge of these 24 D7-branes is supposed to vanish, due to S-duality effects (e.g. Denef 08, below (3.41)).

For analogous discussion of 24 NS5-branes in heterotic string theory on K3 see Schwarz 97, around p. 50.

For more see at 24 branes transverse to K3.

F-brane scan

from M-branes to F-branes: superstrings, D-branes and NS5-branes

M-theory on $S^1_A \times S^1_B$-elliptic fibration	KK-compactification on $S^1_A$	type IIA string theory	T-dual KK-compactification on $S^1_B$	type IIB string theory	geometrize the axio-dilaton	F-theory on elliptically fibered-K3 fibration	duality between F-theory and heterotic string theory	heterotic string theory on elliptic fibration
M2-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	type IIA superstring	$\mapsto$	type IIB superstring	$\mapsto$	“	$\mapsto$	heterotic superstring
M2-brane wrapping $S_B^1$	$\mapsto$	D2-brane	$\mapsto$	D1-brane	$\mapsto$	“
M2-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ strings and $q$ D2-branes	$\mapsto$	(p,q)-string	$\mapsto$	“
M5-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	D4-brane	$\mapsto$	D5-brane	$\mapsto$	“
M5-brane wrapping $S_B^1$	$\mapsto$	NS5-brane	$\mapsto$	NS5-brane	$\mapsto$	“	$\mapsto$	NS5-brane
M5-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ D4-brane and $q$ NS5-branes	$\mapsto$	(p,q)5-brane	$\mapsto$	“
M5-brane wrapping $S_A^1 \times S_B^1$	$\mapsto$		$\mapsto$	D3-brane	$\mapsto$	“
KK-monopole/A-type ADE singularity (degeneration locus of $S^1_A$-circle fibration, Sen limit of $S^1_A \times S^1_B$ elliptic fibration)	$\mapsto$	D6-brane	$\mapsto$	D7-branes	$\mapsto$	A-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 2)		SU-gauge enhancement
KK-monopole orientifold/D-type ADE singularity	$\mapsto$	D6-brane with O6-planes	$\mapsto$	D7-branes with O7-planes	$\mapsto$	D-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 3)		SO-gauge enhancement
exceptional ADE-singularity	$\mapsto$		$\mapsto$		$\mapsto$	exceptional ADE-singularity of elliptic fibration	$\mapsto$	E6-, E7-, E8-gauge enhancement

(e.g. Johnson 97, Blumenhagen 10)

S-duality operation on $(p,q)$-branes

The F-theory picture gives a geometric interpretation of the S-duality expected in type II string theory, by which all branes carry two integer charges $(p,q)$ acted on by $SL(2,\mathbb{Z})$. For instance the fundamental string (F1-brane) and the D1-brane combine to the $(p,q)$-string, and similarly the NS5-brane and the D5-brane combine to a $(p,q)$-5-brane.

Namely in the F-theory picture this comes from wrapping the M2-brane and the M5-brane, respectively, on either of the two cycles of the elliptic fibration (and the T-dualizing).

(e.g. Johnson 97, p. 4)

Model building and phenomenology

For F-theory a fairly advanced model building and string phenomenology has been developed. A detailed review is in (Denef 08).

Via the relation between supersymmetry and Calabi-Yau manifolds there is particular interest in F-theory compactified on Calabi-Yau spaces of (complex) dimension 4. For more on this see at F/M-theory on elliptically fibered Calabi-Yau 4-folds.

A large number of realizations of the exact field content of the standard model of particle physics (or rather the MSSM) is claimed to be realized in in F-theory in Cvetic-Halverson-Lin-Liu-Tian 19.

Related concepts

• F'-theory

• D=12 supergravity, D=14 supersymmetry, bosonic M-theory

F-theory KK-compactified on elliptically fibered complex analytic fiber $\Sigma$

$dim_{\mathbb{C}}(\Sigma)$	1	2	3	4	5
	F-theory	F-theory on CY2	F-theory on CY3	F-theory on CY4	F-theory on CY5

• F-theory on Spin(7)-manifolds

References

General

Discussion of T-duality in the strong coupling limit is due to

• John Schwarz: M Theory Extensions of T Duality, in: Frontiers in Quantum Field Theory, World Scientific (1996) 3-14 [arXiv:hep-th/9601077, doi:10.1142/3245]

• Jorge Russo, T-duality in M-theory and supermembranes, Phys.Lett. B400 (1997) 37-42 (arXiv:hep-th/9701188)

That S-duality of type II string theory may be interpreted in terms of conformal transformations on the fiber for M-theory compactified on a torus was originally observed in

• John Schwarz: An $SL(2,\mathbb{Z})$-Multiplet of Type IIB Superstrings, Phys. Lett. B 360 (1995) 13-18 ERRATUM-ibid. B 364 (1995) 252 [arXiv:hep-th/9508143]

• Paul Aspinwall, Some Relationships Between Dualities in String Theory, Nucl. Phys. Proc. Suppl. 46 (1996) 30-38 [arXiv:hep-th/9508154, doi:10.1016/0920-5632(96)00004-7]

The original article on F-theory as such is

• Cumrun Vafa, Evidence for F-theory, Nucl. Phys. B469:403-418, 1996, (arXiv:hep-th/9602022)

An early survey of its relation to M-theory with M5-branes is in

• Clifford Johnson: From M-theory to F-theory, with Branes, Nucl. Phys. B 507 (1997) 227-244 [arXiv:hep-th/9706155, doi:10.1016/S0550-3213(97)00550-6]

A more recent survey is

• Ralph Blumenhagen, Basics of F-theory from the Type IIB Perspective (arXiv:1002.2836)

Lecture notes include

• David Morrison, TASI Lectures on Compactification and Duality (arXiv:hep-th/0411120)

• Timo Weigand, Lectures on F-theory compactifications and model building Class. Quantum Grav. 27 214004 (arXiv:1009.3497)

• Timo Weigand, TASI Lectures on F-theory (arXiv:1806.01854)

Textbook accounts include

• Katrin Becker, Melanie Becker, John Schwarz, section 8.4 of: String Theory and M-Theory: A Modern Introduction, Cambridge University Press 2007 (doi:10.1017/CBO9780511816086)

Further survey includes

• Timo Weigand, F-theory: Progress and Prospects, 2014 (pdf)

• Cumrun Vafa, Reflections on F-theory, 2015 (pdf)

Related conferences include

• Physics and Geometry of F-theory 2014

• Physics and Geometry of F‑theory 2015

Relation to orientifolds

F-theory lifts of orientifold backgrounds were first identified in

• Ashoke Sen, F-theory and Orientifolds, Nucl. Phys. B475:562-578,1996 (arXiv:hep-th/9605150)

• Ashoke Sen, Orientifold Limit of F-theory Vacua, Nucl. Phys. Proc. Suppl. 68 (1998) 92 (Nucl. Phys. Proc. Suppl. 67 (1998) 81) (arXiv:hep-th/9702165)

and the corresponding gauge enhancement in

• Ashoke Sen, A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)

with more details including

• Zurab Kakushadze, Gary Shiu, S.-H. Henry Tye, Type IIB Orientifolds, F-theory, Type I Strings on Orbifolds and Type I - Heterotic Duality, Nucl.Phys. B533 (1998) 25-87 (arXiv:hep-th/9804092)

This is further expanded on in

• Hisham Sati, The Elliptic curves in gauge theory, string theory, and cohomology, JHEP 0603 (2006) 096 (arXiv:hep-th/0511087)

Relation to elliptic cohomology

A series of articles arguing for a relation between the elliptic fibration of F-theory and elliptic cohomology (see also at modular equivariant elliptic cohomology)

• Igor Kriz, Hisham Sati, Type II string theory and modularity, JHEP 0508 (2005) 038 (arXiv:hep-th/0501060)

Relation to heterotic string string theory

• Robert Friedman, John Morgan, Edward Witten, Vector Bundles And F Theory (arXiv:hep-th/9701162)

• Ron Donagi, ICMP lecture on heterotic/F-theory duality (arXiv:hep-th/9802093)

Relation to M-theory on $G_2$-manifolds

• Sergei Gukov, Shing-Tung Yau, Eric Zaslow, Duality and Fibrations on $G_2$ Manifolds (arXiv:hep-th/0203217)

• Adil Belhaj, F-theory Duals of M-theory on $G_2$ Manifolds from Mirror Symmetry (arXiv:hep-th/0207208)

• Mariana Graña, C. S. Shahbazi, Marco Zambon, $Spin(7)$-manifolds in compactifications to four dimensions, JHEP11(2014)046 (arXiv:1405.3698)

Relation to the 6d superconformal theory

Realization to the 6d (2,0)-supersymmetric QFT is discussed in

• Jonathan Heckman, David Morrison, Cumrun Vafa, On the Classification of 6D SCFTs and Generalized ADE Orbifolds (arXiv:1312.5746)

Phenomenology and model building

A large body of literature is concerned with particle physics string phenomenology modeled in the context of F-theory, in particular GUTs:

• Frederik Denef, Les Houches Lectures on Constructing String Vacua, in: String theory and the real world (arXiv:0803.1194, spire:780946)

• Chris Beasley, Jonathan Heckman, Cumrun Vafa, GUTs and Exceptional Branes in F-theory - I, JHEP 0901:058,2009 (arXiv:0802.3391)

• Chris Beasley, Jonathan Heckman, Cumrun Vafa, GUTs and Exceptional Branes in F-theory - I (arxiv:0802.3391), II: Experimental Predictions (arxiv:0806.0102)

• Martin Wijnholt, String compactification, PITP 2014 lecture notes (pdf, slides for lecture 1, slides for lecture 2, slides for lecture 3)

• Gianluca Zoccarato, Yukawa couplings at the point of $E_8$ in F-theory, 2014 (pdf/zoccarato.pdf))

Discussion of the exact gauge group of the standard model of particle physics, $G = \big( SU(3) \times SU(2) \times U(1)\big)/\mathbb{Z}_6$ including its $\mathbb{Z}_6$-quotient (see there) and the exact fermion field content, realized in F-theory is in

• Denis Klevers, Damian Kaloni Mayorga Pena, Paul-Konstantin Oehlmann, Hernan Piragua, Jonas Reuter, F-Theory on all Toric Hypersurface Fibrations and its Higgs Branches, JHEP01(2015)142 (arXiv:1408.4808)

• Mirjam Cvetic, Ling Lin, section 3.3 of The global gauge group structure of F-theory compactifications with $U(1)$s (arXiv:1706.08521)

Based on this large number of realizations of the exact field content of the standard model of particle physics (or rather MSSM) in F-theory is claimed to be realized in

• Mirjam Cvetic, James Halverson, Ling Lin, Muyang Liu, Jiahua Tian, A Quadrillion Standard Models from F-theory (arXiv:1903.00009)

• Washington Taylor, Andrew P. Turner, Generic construction of the Standard Model gauge group and matter representations in F-theory (arXiv:1906.11092)

Review:

• Fernando Marchesano, Bert Schellekens, Timo Weigand, D-brane and F-theory Model Building, in Handbook of Quantum Gravity, Springer (2023) [arXiv:2212.07443]

Realization of $E_7$-GUT models in F-theory:

• Shing Yan Li, Washington Taylor, Towards natural and realistic $E_7$ GUTs in F-theory [arXiv:2401.00040]

Cosmological constant

An argument for non-perturbative non-supersymmetric 4d string phenomenology with fundamentally vanishing cosmological constant, based on 3d M-theory on 8-manifolds decompactified at strong coupling to 4d via duality between M-theory and type IIA string theory (recall the super 2-brane in 4d):

• Edward Witten, The Cosmological Constant From The Viewpoint Of String Theory, lecture at DM2000 (arXiv:hep-ph/0002297)

  (see p. 7)

• Edward Witten, Strong coupling and the cosmological constant, Mod. Phys. Lett. A 10:2153-2156, 1995 (arXiv:hep-th/9506101)

• Edward Witten, Section 3 of Some Comments On String Dynamics, talk at Strings95 (arXiv:hep-th/9507121)

The realization of this scenario in F-theory:

• Cumrun Vafa, Section 4.3 of: Evidence for F-Theory, Nucl. Phys. B469:403-418, 1996 (arxiv:hep-th/9602022)

• Jonathan Heckman, Craig Lawrie, Ling Lin, Gianluca Zoccarato, F-theory and Dark Energy, Fortschritte der Physik (arXiv:1811.01959, doi:10.1002/prop.201900057)

• Jonathan Heckman, Craig Lawrie, Ling Lin, Jeremy Sakstein, Gianluca Zoccarato, Pixelated Dark Energy (arXiv:1901.10489)

Flavour anomalies

Realization in F-theory of GUT-models with Z'-bosons and/or [leptoquarks]] addressing the flavour anomalies and the (g-2) anomalies:

• Miguel Crispim Romao, Stephen F. King, George K. Leontaris, Non-universal $Z'$ from Fluxed GUTs, Physics Letters B Volume 782, 10 July 2018, Pages 353-361 (arXiv:1710.02349)

• A. Karozas, G. K. Leontaris, I. Tavellaris, N. D. Vlachos, On the LHC signatures of $SU(5) \times U(1)'$ F-theory motivated models (arXiv:2007.05936)

4-Form flux and instantons

The image of the supergravity C-field from 11-dimensional supergravity to F-theory yields the $G_4$-flux.

• Andres Collinucci, Raffaele Savelli, On Flux Quantization in F-Theory (2010) (arXiv:1011.6388)

• Sven Krause, Christoph Mayrhofer, Timo Weigand, $G_4$ flux, chiral matter and singularity resolution in F-theory compactifications (arXiv:1109.3454)

• Thomas Grimm, Denis Klevers, Maximilian Poretschkin, Fluxes and Warping for Gauge Couplings in F-theory (arXiv:1202.0285)

• Sven Krause, Christoph Mayrhofer, Timo Weigand, Gauge Fluxes in F-theory and Type IIB Orientifolds (2012) (arXiv:1202.3138)

and with M5-brane instanton contributions:

• Max Kerstan, Timo Weigand, Fluxed M5-instantons in F-theory (arXiv:1205.4720)

Reviewed in

• Timo Weigand, Fluxes and M5-instantons in F-theory, 2012 (pdf slides)

For more on this see also at F/M-theory on elliptically fibered Calabi-Yau 4-folds.