nLab topological vector bundle
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Bundles
Context
Classes of bundles
-
vector bundle, 2-vector bundle, (∞,1)-vector bundle
real, complex/holomorphic, quaternionic
Universal bundles
Presentations
Examples
Constructions
Linear algebra
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
A topological vector bundle is a vector bundle in the context of topology: a continuously varying collection of vector space over a given topological space.
For more survey and motivation see at vector bundle. Here we discuss the details of the general concept in topology. See also differentiable vector bundle and algebraic vector bundle.
Definition
We first give the more abstract definiton in terms of slice categories (def. below) and then unwind this to the traditional definition (def below).
In the following
-
is either the topological field
-
of real numbers
-
or of complex numbers
equipped with the Euclidean metric topology.
-
In terms of slice categories
Definition
(topological vector bundles in terms of slice categories)
Write Top for the category of topological spaces, and for a space, write for its slice category over . The Cartesian product in is the fiber product over in , which we denote by . Observe is canonically a field internal to
A topological vector bundle over is
-
an object of
-
with the structure of an -vector space-object internal to , hence
-
a morphism
-
a morphism
which satisfy the vector space axioms
-
such that
-
(local triviality) there exists
-
an open cover , regarded via the disjoint union space of the patches as the object ,
-
an isomorphism of vector space objects in
for some , where and are regarded as a vector space objects in in the canonical way.
-
It follows that is constant on connected components. Often this is required to be constant on all of and then called the rank of the vector bundle.
A homomorphism of topological vector bundles is simple a homomorphism of vector space objects in .
Topological vector bundles over and homomorphisms between them constitutes a category, usually denoted Vect(X).
Notice that viewed in Top, the last condition means that there is a diagram of the form
where the square is a pullback square and the homeomorphism in the top left is fiber-wise linear.
If we say this yet more explicitly, it yields the definition as found in the traditional textbooks:
In components
Definition
(topological vector bundle in components)
Let be a topological space. Then a topological vector bundle over is
-
for each the stucture of a finite-dimensional -vector space on the pre-image
such that this is locally trivial in that there exists
-
an open cover ,
-
for each an and a homeomorphism
from the product topological space of with the real numbers (equipped with their Euclidean space metric topology) to the restriction of over , such that
-
is a map over in that , hence in that
-
is a linear map in each fiber in that
-
Often, but not always, it is required that the numbers are all equal to some , for all , hence that the vector space fibers all have the same dimension. In this case one says that the vector bundle has rank . (Over a connected topological space this is automatic, but the fiber dimension may be distinct over distinct connected components.)
For and two topological vector bundles over the same base space, then a homomorphism between them is
such that
-
respects the projections: ;
-
for each we have that is a linear map.
Remark
(category of topological vector bundles)
For a topological space, there is the category whose
-
objects are the topological vector bundles over ,
-
morphisms are the topological vector bundle homomorphisms
according to def. . This category usually denoted Vect(X).
We write for the set of isomorphism classes of this category.
Remark
(fiberwise operations)
The category FinDimVect of finite dimensional vector spaces over a topological ground field is canonically a Top-enriched category, and so are hence its product categories , for . Any Top-enriched functor
induces a functorial construction of new topological vector bundles from any n-tuple of vector bundles over the same base space , by taking the new fiber over a point to be (e.g. Milnor & Stasheff 1974, p. 32):
For example:
-
if is the operation of forming dual vector spaces, then constructs the fiberwise dual vector bundle;
-
if is the operation of forming determinants, then is the construction of fiberwise determinant line bundles;
-
if is the direct sum of vector space, then constructs the fiberwise direct sum of vector bundles (“Whitney sum”);
-
if is the tensor product of vector spaces, then constructs the fiberwise tensor product of vector bundles.
Remark
(some terminology)
For one speaks of real vector bundles.
For one speaks of complex vector bundles.
For one speaks of line bundles, in particular of real line bundles and of complex line bundles.
Remark
(any two topologial vector bundles have local trivialization over a common open cover)
Let and be two topological vector bundles (def. ). Then there always exists an open cover such that both bundles have a local trivialization over this cover.
Proof
By definition we may find two possibly different open covers and with local tivializations and .
The joint refinement of these two covers is the open cover
The original local trivializations restrict to local trivializations on this finer cover
and
Example
(trivial topological vector bundle and (local) trivialization)
For any topological space, and , we have that the product topological space
canonically becomes a topological vector bundle over (def. ). This is called the trivial vector bundle of rank over .
Given any topological vector bundle , then a choice of isomorphism to a trivial bundle (if it exists)
is called a trivialization of . A vector bundle for which a trivialization exists is called trivializable.
Accordingly, the local triviality condition in the definition of topological vector bundles (def. ) says that they are locally isomorphic to the trivial vector bundle. One also says that the data consisting of an open cover and the homeomorphisms
as in def. constitute a local trivialization of .
Example
(section of a topological vector bundle)
Let be a topological vector bundle (def. ).
Then a homomorphism of vector bundles from the trivial line bundle (example , remark )
is, by fiberwise linearity, equivalently a continuous function
such that ;
Such functions are called sections (or cross-sections) of the vector bundle .
Example
(topological vector sub-bundle)
Given a topological vector bundel (def. ), then a sub-bundle is a homomorphism of topological vector bundles over
such that for each point this is a linear embedding of fibers
(This is a monomorphism in the category of topological vector bundles over .)
Transition functions and Cech cohomology
We discuss how topological vector bundles are equivalently given by cocycles in Cech cohomology constituted by their transition functions.
Definition
(continuous functions on open subsets with values in the general linear group)
For , regard the general linear group as a topological group with its standard topology, given as the Euclidean subspace topology via or as the or as the subspace topology of the compact-open topology on the mapping space. (That these topologies coincide is the statement of this prop..
For a topological space, we write
for the assignment that sends an open subset to the set of continuous functions (for equipped with its subspace topology), regarded as a group via the pointwise group operation in :
Moreover, for an inclusion of open subsets, and for , we write
for the restriction of the continuous function from to .
Remark
In the language of category theory the assignment from def. of continuous functions to open subsets and the restriction operations between these is called a sheaf of groups on the site of open subsets of .
Definition
Given a topological vector bundle as in def. and a choice of local trivialization (example ) there are for induced continuous functions
to the general linear group (as in def. ) given by composing the local trivialization isomorphisms:
These are called the transition functions for the given local trivialization.
These functions satisfy a special property:
Definition
Let be a topological space.
A normalized Cech cocycle of degree 1 with coefficients in (def. ) is
-
an open cover
such that
-
(normalization) (the constant function on the neutral element in ),
-
(cocycle condition) .
Write
for the set of all such cocycles for given and write
for the disjoint union of all these cocycles as varies.
Example
(transition functions are Cech cocycles)
Let be a topological vector bundle (def. ) and let , be a local trivialization (example ).
Then the set of induced transition functions according to def. is a normalized Cech cocycle on with coefficients in , according to def. .
Proof
This is immediate from the definition:
and
Conversely:
Example
(topological vector bundle constructed from a Cech cocycle)
Let be a topological space and let a Cech cocycle on according to def. , with open cover and component functions .
This induces an equivalence relation on the product topological space
(of the disjoint union space of the patches regarded as topological subspaces with the product space ) given by
Write
for the resulting quotient topological space. This comes with the evident projection
which is a continuous function (by the universal property of the quotient topological space construction, since the corresponding continuous function on the un-quotientd disjoint union space respects the equivalence relation). Moreover, each fiber of this map is identified with , and hence canonicaly carries the structure of a vector space.
Finally, the quotient co-projections constitute a local trivialization of this vector bundle over the given open cover.
Therefore is a topological vector bundle (def. ). We say it is the topological vector bundle glued from the transition functions.
Remark
(bundle glued from Cech cocycle is a coequalizer)
Stated more category theoretically, the constructure of a topological vector bundle from Cech cocycle data in example is a universal construction in topological spaces, namely the coequalizer of the two morphisms
in the category of vector space objects in the slice category . Here the restriction of to the coproduct summands is induced by inclusion:
and the restriction of to the coproduct summands is via the action of the transition functions:
In fact, extracting transition functions from a vector bundle by def. and constructing a vector bundle from Cech coycle data as above are operations that are inverse to each other, up to isomorphism.
Proposition
(topological vector bundle reconstructed from its transition functions)
Let be a topological vector bundle (def. ), let be an open cover of the base space, and let be a local trivialization.
Write
for the corresponding transition functions (def. ). Then there is an isomorphism of vector bundles over
from the vector bundle glued from the transition functions according to def. to the original bundle , whose components are the original local trivialization isomorphisms.
Proof
By the universal property of the disjoint union space (coproduct in Top), continuous functions out of them are equivalently sets of continuous functions out of every summand space. Hence the set of local trivializations may be collected into a single continuous function
By construction this function respects the equivalence relation on the disjoint union space given by the transition functions, in that for each we have
By the universal property of the quotient space coprojection this means that uniquely extends to a continuous function on the quotient space such that the following diagram commutes
It is clear that this continuous function is a bijection. Hence to show that it is a homeomorphism, it is now sufficient to show that this is an open map (by this prop.).
So let be an subset in the quotient space which is open. By definition of the quotient topology this means equivalently that its restriction to is open for each . Since the are homeomorphsms, it follows that the images are open. By the nature of the subspace topology, this means that these images are open also in . Therefore also the union is open.
Definition
(coboundary between Cech cocycles )
Let be a topological space and let be two Cech cocycles (def. ), given by
-
and two open covers,
-
and the corrsponding component functions.
Then a coboundary between these two cocycles is
-
the condition that ,
-
an open cover ,
-
functions and such that
such that
-
,
hence such that the following diagrams of linear maps commute for all and :
Say that two Cech cocycles are cohomologous if there exists a coboundary between them.
Example
(refinement of a Cech cocycle is a coboundary)
Let be a topological space and let be a Cech cocycle as in def. , with respect to some open cover given by component functions .
Then for a refinement of the given open cover, hence an open cover such that there exists a function with , then
are the components of a Cech cocycle which is cohomologous to .
Proposition
(isomorphism of topological vector bundles induces Cech coboundary between their transition functions)
Let be a topological space, and let be two Cech cocycles as in def. .
Every isomorphism of topological vector bundles
between the vector bundles glued from these cocycles according to def. induces a coboundary between the two cocycles,
Proof
By example we may assume without restriction that the two Cech cocycles are defined with respect to the same open cover (for if they are not, then both are cohomologous to cocycles on a joint refinement of the original covers and we may argue with these).
Accordingly, by example the two bundles and both have local trivializations of the form
and
over this cover. Consider then for the function
hence the unique function making the following diagram commute:
This induces for all the following composite commuting diagram
By construction, the two horizonal composites of this diagram are pointwise given by the components and of the cocycles and , respectively. Hence the commutativity of this diagram is equivalently the commutativity of these diagrams:
for all and . By def. this exhibits the required coboundary.
Definition
Let be a topological space. The relation on Cech cocycles of being cohomologous (def. ) is an equivalence relation on the set of Cech cocycles (def. ).
Write
for the resulting set of equivalence classes. This is called the Cech cohomology of in degree 1 with coefficients in .
Proposition
(degree-1 Cech cohomology computes topological vector bundles)
Let be a topological space.
The construction of gluing a topological vector bundle from a Cech cocycle (example ) constitutes a bijection between the degree-1 Cech cohomology of with coefficients in (def. ) and the set of isomorphism classes of topological vector bundles on (def. , remark ):
Proof
First we need to see that the function is well defined, hence that if cocycles are related by a coboundary, (def. ), then the vector bundles and are related by an isomorphism.
Let be the open cover with respect to which the coboundary is defined, with refining functions and . Let and be the corresponding restrictions of the canonical local trivilizations of the two glued bundles.
For define
Observe that for and the coboundary condition implies that
because in the diagram
the vertical morphism in the middle on the right is unique, by the fact that all other morphisms in the diagram on the right are invertible.
Therefore there is a unique vector bundle homomorphism
given for all by . Similarly there is a unique vector bundle homomorphism
given for all by . Hence this is the required vector bundle isomorphism.
Finally to see that the function from Cech cohomology classes to isomorphism classes of vector bundles thus defined is a bijection:
By prop. the function is surjective, and by prop. it is injective.
Examples
Example
For then the projective space carries the tautological line bundle whose fiber over the -line is that -line.
For details see there
Example
(cylinder)
Let
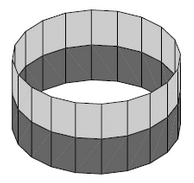
be the circle with its Euclidean subspace metric topology.
Then the trivial real line bundle on the circle is the the cylinder
Example
Let
be the circle with its Euclidean subspace metric topology. Consider the open cover
with
for any .
Define a Cech cohomology cocycle (remark ) on this cover by
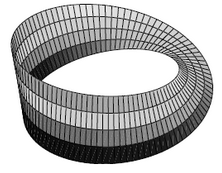
Since there are no non-trivial triple intersections, all cocycle conditions are evidently satisfied.
Accordingly by example these functions define a vector bundle. This is the Moebius strip
Example
(basic complex line bundle on the 2-sphere)
Let
be the 2-sphere with its Euclidean subspace metric topology. Let
be the two complements of antipodal points
Define continuous functions
Since there are no non-trivial triple intersections, the only cocycle condition is
which is clearly satisfied.
The complex line bundle this defined is called the basic complex line bundle on the 2-sphere.
With the 2-sphere identified with the complex projective space (the Riemann sphere), the basic complex line bundle is the tautological line bundle (example ) on .
Example
Generally, for , then the n-sphere may be covered by two open hemispheres intersecting in an equator of the form . A vector bundle is then defined by specifying a single function
This is called the clutching construction of vector bundles over n-spheres.
Example
For the topological space underlyithe ng a differentiable manifold then its tangent bundle is a real vector bundle over whose rank is the dimension of .
Example
For an embedding of differentiable manifolds, then the normal bundle
is the real vector bundle over whose fiber at is the quotient vector space .
Properties
Basic properties
Lemma
(homomorphism of vector bundles is isomorphism as soon as it is a fiberwise isomorphism)
Let and be two topological vector bundles (def. ).
If a homomorphism of vector bundles restricts on the fiber over each point to a linear isomorphism
then is already an isomorphism of vector bundles.
Proof
It is clear that has an inverse function of underlying sets which is a function over : Over each it it the linear inverse .
What we need to show is that this is a continuous function.
By remark we find an open cover over which both bundles have a local trivialization.
Restricted to any patch of this cover, the homomorphism induces a homomorphism of trivial vector bundles
Also the are fiberwise invertible, hence are continuous bijections. We claim that these are homeomorphisms, hence that their inverse functions are also continuous.
To this end we re-write the a little. First observe that by the universal property of the product topological space and since they fix the base space , the are equivalently given by a continuous function
as
Moreovern since is locally compact (like every finite dimensional vector space, by the Heine-Borel theorem), the mapping space adjunction says (by this prop.) that there is a continuous function
(with the set of continuous functions equipped with the compact-open topology) which factors via the evaluation map as
By assumption of fiberwise linearity the functions in fact take values in the general linear group
and this inclusion is a homeomorphism onto its image (by this prop.).
Since passing to inverse matrices
is a rational function on its domain inside Euclidean space and since rational functions are continuous on their domain of definition, it follows that the inverse of
is a continuous function.
To conclude that also is a continuous function we make use prop. to find an isomorphism between and a quotient topological space of the form
Hence is equivalently a function on this quotient space, and we need to show that as such it is continuous.
By the universal property of the disjoint union space (the coproduct in Top) the set of continuous functions
corresponds to a single continuous function of the form
These functions respect the equivalence relation, since for each we have
Therefore by the universal property of the quotient topological space , these functions extend to a unique continuous function such that the following diagram commutes:
This unique function is clearly (by pointwise inspection) and therefore is continuous.
Example
(fiberwise linearly independent sections trivialize a vector bundle)
If a topological vector bundle of rank admits sections (example )
that are linearly independent at each point , then is trivializable (example ). In fact, with the sections regarded as vector bundle homomorphisms out of the trivial vector bundle of rank (according to example ), these sections are the trivialization
This is because their linear independence at each point means precisely that this morphism of vector bundles is a fiber-wise linear isomorphsm and therefore an isomorphism of vector bundles by lemma .
Direct summand bundles
We discuss properties of the direct sum of vector bundles for topological vector bundles.
Proposition
(sub-bundles over paracompact spaces are direct summands)
Let
-
a topological vector bundle (def. ).
Then every topological vector sub-bundle (example ) is a direct vector bundle summand, in that there exists another vector sub-bundle (example ) such that their direct sum of vector bundles is :
Proof
Since is assumed to be paracompact Hausdorff, there exists an inner product on vector bundles
(by this prop.). This defines at each the orthogonal complement of . The subspace of these orthogonal complements is readily checked to be a topological vector bundle . Hence by construction we have
Proposition
(vector bundles over a compact Hausdorff space are direct summands of a trivial vector bundle)
Let
-
be a compact Hausdorff space;
-
a topological vector bundle (def. ).
Then there exists another topological vector bundle such that the direct sum of vector bundles of the two is isomorphic to a trivial vector bundle :
Proof
Let be an open cover of over which has a local trivialization
By compactness of , there is a finite sub-cover, hence a finite set such tat
is still an open cover over which trivializes.
Since paracompact Hausdorff spaces equivalently admit subordinate partitions of unity there exists a partition of unity
with support . Hence the functions
extend by 0 to vector bundle homomorphism of the form
The finite pointwise direct sum of these yields a vector bundle homomorphism of the form
Observe that, as opposed to the single , this is a fiber-wise injective, because at each point at least one of the is non-vanishing. Hence this is an injection of into a trivial vector bundle.
Remark
Prop. is key in the analysis of topological K-theory groups on compact Hausdorff spaces. See there for more.
Concordance
We discuss that every concordance of topological vector bundles over a paracompact topological space makes the restriction of the vector bundle over the endpoints of the interval isomorphic (prop. below). In particular this implies tht the pullbacks of vector bundles along two homotopic continuous functions are isomorphic (corollary below).
This result is apparently due to Steenrod, see Theorem 11.4 in Steenrod. The proof below follows Hatcher, theorem 1.6.
For a topological space write for the product topological space with the closed interval equipped with its Euclidean metric topology.
Write
for the two continuous projections out of the product space.
Lemma
For a topological space, then a vector bundle is trivializable (example ) if its restrictions to and to are trivializable.
Lemma
For a topological space, then for every topological vector bundle there exists an open cover of such that the vector bundle trivializes over , for each .
Proof
By local trvializability of the vector bundle, there exists an open cover over which the bundle trivializes. For each point this induces a cover of . This is a compact topological space (for instance by the Heine-Borel theorem) and hence there exists a finite subset such that still covers .
By finiteness of , the intersection
is an open neighbourhood of in . Moreover
is an open cover of such that the given vector bundle trivializes over each element of .
By the nature of the Euclidean metric topology each open subset of is a union of intervals. So we may pass to a refinement of this cover of such that each element is a single interval. Again by compactness of , this refinement has a finite subcover
each element of which is an interval. Since this is a finite cover, we may find numbers such that
is a cover of , and such that the given vector bundle still trivializes over for all .
By lemma this implies that the vector bundle in fact trivializes over .
Applying this procedure for all points yields a cover
with the required property.
Proposition
(concordance of topological vector bundles)
Let be a paracompact Hausdorff space. If is a topological vector bundle over the product space of with the closed interval (hence a concordance of topological vector bundles on ), then the two endpoint-restrictions
are isomorphic vector bundles over .
Proof
By lemma there exists an open cover of such that the vector bundle trivializes over for each . By this lemma there exists a countable cover
such that each element is a disjoint union of open subsets that each are contained in one of the . This means that the vector bundle still trivializes over , for each .
Moreover, since paracompact Hausdorff spaces equivalently admit subordinate partitions of unity, there exists a partition of unity subordinate to this countable cover.
For define
(so and by local finiteness there is for each an such that .)
Now write
for the graph of the function equipped with its subspace topology, and write
for the restriction of to that subspace
Observe that the projection functions
are continuous functions: By the nature of the product topology and the subspace topology it is sufficient to check for and open subsets, that every point in the preimage is contained in an open subset of the form such that every point of that is also in is still mapped to . Such an open subset is .
Also observe that the composites
make each a vector bundle over : To see local trivializability over choose a local trivialization of over some open cover and observe that then is trivial over the fiber product and hence over .
Now by the pullback definition of the , the pasting law says that for each we have a pullback square of vector bundles of the form
By the nature of pullbacks, the top horizontal function in this diagram is on each fiber a linear isomorphism. Therefore prop. implies that each is in fact an isomorphism of vector bundles over
By local finiteness, each point has a neighbourhood such that only a finite number of these are non-trivial, and so it makes sense to consider the infinite composition
understood to be on each the finite composite
Since all the are vector bundle isomorphisms, so are all their composites. Thus is an isomorphism of the required form
Corollary
Let be a paracompact Hausdorff space, let be a topological vector bundle, let be two continuous functions, and let be a left homotopy between them. Then there is an isomorphism of vector bundles over between the pullback of vector bundles of along and along , respectively:
Proof
By definition, the left homotopy is a continuous function of the form
For write for the continuous function
By the pasting law for pullbacks we have that
and
Example
(homotopy invariance of isomorphism classes of vector bundles)
Let and be paracompact Hausdorff spaces and let
be a continuous function which is a homotopy equivalence. Then pullback along constitutes a bijection on sets of isomorphism classes of topological vector bundles:
Proof
By definition of homotopy equivalence, there is a continuous function and left homotopies
This mean that is the inverse function to , and hence both are bijections.
Example
(topological vector bundle on contractible topological space is trivializable)
If is a contractible topological space, then every topological vector bundle over is isomorphic to a trivial vector bundle.
Proof
That is contractible means by definition that there is a left homotopy of the form
By cor it follows that for any topological vector bundle that there is an isomorphism between and the result of first restricting the bundle to the point, and then forming the pullback bundle along . But the latter operation precisely produces the trivial vector bundles over .
Over closed subspaces
We discuss the behavour of vector bundles with respect to closed subspaces of compact Hausdorff spaces.
Lemma
(isomorphism of vector bundles on closed subset of compact Hausdorff spaces extends to open neighbourhood)
Let , let be a compact Hausdorff space and let a closed subspace. Let be two topological vector bundles over , .
If there exists an isomorphism
of the restricted vector bundles over , then there also exists an open subset with such that there is also an isomorphism
of the vector bundles restricted to .
Proof
A bundle isomorphism is equivalently a trivializing section (example ) of the tensor product of vector bundles of with the dual vector bundle . (by this prop.).
Let be an open cover of over which this tensor product bundle trivializes with trivializations
Since compact Hausdorff spaces are normal, the shrinking lemma applies and gives a refinement of this by a cover by closed subsets .
Then a trivializing section as above is on each a continuous function
to the general linear group , such that
Regarded as a function to the matrices, this is a set of continuous function
Now since is closed by construction, and is closed by assumption, also the intersections are closed. Since compact Hausdorff spaces are normal the Tietze extension theorem therefore applies to these component functions and yields extensions of each to a continuous function of the form
Moreover, since compact Hausdorff spaces are evidently paracompact Hausdorff spaces, and since paracompact Hausdorff spaces equivalently admit subordinate partitions of unity, it follows that we find a partition of unity .
Consider then the functions given by pointwise multiplication and regarded, via extension by zero, as continuous functions on all of
Summing these up yields a single section of
which by construction is an extension of the original section, in that
This is because for each we have, using the above definitions,
Here the last step uses the nature of the partition of unity.
Now while is an extension of the section to , it will in general not be a trivializing section on .
But since the general linear group is an open subset of the Euclidean space , it follows that each point has an open neighbourhood such that is still a trivializing section, namely choosing such that set
The union of these
is hence an open subset containing such that has a trivializing section, extending , hence such that there is an isomorphism extending the original isomorphism on .
As a consequence:
Proposition
(vector bundle trivial over closed subspace of compact Hausdorff space is pullback of bundle on quotient space)
Let be a compact Hausdorff space and let be a closed subspace.
If a topological vector bundle is such that its restriction is trivializable, then is isomorphic to the pullback bundle of a topological vector bundle over the quotient space.
Proof
Let
be an isomorphism of vector bundles over , which exists by assumption. Consider then on the total space the equivalence relation given by
for all and . Let
be the corresponding quotient topological space. Observe that for we have while for we have a canonical identification , and over these points quotient coprojection is identified with :
Since the composite continuous function
respects the equivalence relation (in that it sends any two equivalent points to the same image point) the universal property of the quotient space yields a continuous function
such that the following diagram commutes
We claim that this is a pullback diagram in Top:
By the above description of the top horizontal function, it is a pullback diagram of underlying sets. Hence we need to see that the topology on has a base given by the pre-images of the open subsets in and in . Now by definition of the quotient space topology on , its open subsets are those of that either do not contain a point with or if they do, then they also contain all the points of the form for . Moreover, if is in the open subset for , then also for all in some open ball in containing . Hence intersecing these pre-images with pre-images of open subsets of under yields a basis for the topology.
Hence it only remains to see that is a vector bundle. The fiberwise linearity is clear, we need to show that it is locally trivializable.
To that end, let be an open cover over which has a local trivialization. Since is assumed to be closed, it follows that
is an open cover of the complement of in . By the nature of the quotient space topology, this induces an open cover of . If we adjoin the quotient of an open neighbourhood of in , then
is an open cover of . Moreover, by the construction of it is clear that this bundle has a local trivialization over , since does, and similarly trivializes over if trivializes over . But such a does indeed exist by lemma .
Remark
Prop is the reason why reduced topological K-theory satisfies the long exact sequences in cohomology that make it a generalized (Eilenberg-Steenrod) cohomology theory. See
Proposition
Let be a compact Hausdorff space and a closed subspace and write for the corresponding quotient topological space (this example) with quotient coprojection denoted .
If is a contractible topological space then the pullback bundle construction
is an isomorphism.
Proof
By example every vector bundle is trivializable over the contractible subspace . Therefore prop. implies that it is in the image of the pullback bundle map . This says that is surjective. Finally, it is clear that it is injective. Therefore it is bijective.
Example
Let be a pointed compact topological space.
For the closed interval with its Euclidean metric topology.
There is
-
the ordinary cylinder, being the product space
-
the reduced cylinder which is the smash product with the interval that has a base point freely adjoined
and
-
the ordinary suspension ;
-
the reduced suspension .
In both cases the reduced space is obtained from the unreduced space by quotienting out the contractible closed subspace and hence topological vector bundles do not see the difference between the reduced and the unreduced spaces, by prop. .
Related concepts
References
The original reference for many results about bundles, including the theorem that concordance implies isomorphism, is
- Norman Steenrod, The Topology of Fibre Bundles, Princeton University Press (1951, 1957, 1960) [jstor:j.ctt1bpm9t5]
Further textbook accounts:
-
John Milnor, Jim Stasheff, Characteristic classes, Princeton Univ. Press (1974) [ISBN:9780691081229, doi:10.1515/9781400881826, pdf]
-
Glenys Luke, Alexander S. Mishchenko, Vector bundles and their applications, Math. and its Appl. 447, Kluwer 1998. viii+254 pp. MR99m:55019
-
Dale Husemoeller, Michael Joachim, Branislav Jurco, Martin Schottenloher, Basic Bundle Theory and K-Cohomology Invariants, Lecture Notes in Physics, Springer 2008 (pdf)
Lecture notes with an eye towards topological K-theory:
-
Klaus Wirthmüller, Vector bundles and K-theory, 2012 (pdf)
-
Allen Hatcher, chapter 1 of Vector bundles and K-Theory, (partly finished book) web
Last revised on March 30, 2023 at 15:06:05. See the history of this page for a list of all contributions to it.