nLab topological cofiber sequence

under construction

Idea

We discuss in detail the realization of the abstract concept of cofiber sequences in its explicit incarnation in point-set topology, the way it is traditionally presented in topology textbooks.

Hence we use the concepts of homotopy equivalence instead of weak homotopy equivalence. For discussion using the latter in the context of the classical model structure on topological spaces see instead at Introduction to Homotopy Theory the section Homotopy fiber sequences.

Background

Throughout, write $I \coloneqq [0,1] \subset \mathbb{R}$ for the closed interval equipped with its Euclidean metric topology.

Homotopy equivalences

Definition

For $f,g\colon X \longrightarrow Y$ two continuous functions between topological spaces $X,Y$, then a homotopy

$$\eta \colon f \,\Rightarrow_L\, g$$

is a continuous function

$$\eta \;\colon\; X \times I \longrightarrow Y$$

out of the standard cylinder object over $X$: the product space of $X$ with the Euclidean closed interval, such that this fits into a commuting diagram of the form

$$\array{ X \\ {}^{\mathllap{(id,\delta_0)}}\downarrow & \searrow^{\mathrlap{f}} \\ X \times I &\stackrel{\eta}{\longrightarrow}& Y \\ {}^{\mathllap{(id,\delta_1)}}\uparrow & \nearrow_{\mathrlap{g}} \\ X } \,.$$

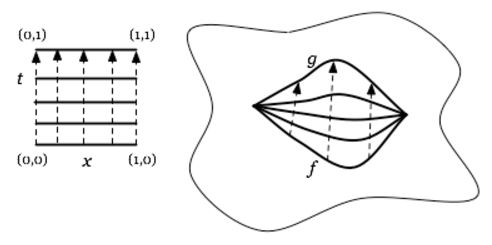
(graphics grabbed from J. Tauber here)

Definition

(homotopy equivalence)

A continuous function $f \colon X \to Y$ is called a homotopy equivalence if there exist

1. a continuous function $g \colon Y \to X$;

2. homotopies (def. ) of the form

   $g \circ f \Rightarrow id_X \phantom{AAAA} f \circ g \Rightarrow id_Y$

Example

(contractible topological space)

A topological space $X$ is called contractible if the unique map to the point space $X \to \ast$ is a homotopy equivalence (def. ).

Cofibrations

Definition

(Hurewicz cofibration)

A continuous function $i \colon A \longrightarrow X$ is called a Hurewicz cofibration or just cofibration if it satisfies the homotopy extension property in that:

• for any topological space $Y$,

• for all continuous functions $f \colon A\to Y$, $\tilde{f}:X\to Y$ such that $\tilde{f}\circ i=f$

  $$\array{ A &\stackrel{f}{\to}& Y \\ {}^{\mathllap{i}}\downarrow & \nearrow_{\mathrlap{\tilde f}} \\ X }$$

• and any left homotopy $F \colon A\times I\to Y$ such that $F(-,0)=f$

there is a homotopy $\tilde{F} \colon X\times I\to Y$ such that

• $\tilde{F}\circ(i\times id_I)=F$

  $$\array{ A \times I &\overset{F}{\longrightarrow}& Y \\ {}^{\mathllap{i \times id_I}}\downarrow & \nearrow_{\mathrlap{\tilde F}} \\ X \times I }$$

• and $\tilde{F}(-,0)=\tilde{f}$

  $$\array{ A &\overset{id_A \times const_0}{\longrightarrow}& A \times I &\overset{F}{\longrightarrow}& Y \\ {}^{\mathllap{i \times id_I}}\downarrow && {}^{\mathllap{i \times id_I}}\downarrow & \nearrow_{\mathrlap{\tilde F}} \\ X &\underset{id_X \times const_0}{\longrightarrow}& X \times I } \phantom{AAA} = \phantom{AAA} \array{ \array{ A &\stackrel{f}{\to}& Y \\ {}^{\mathllap{i}}\downarrow & \nearrow_{\mathrlap{\tilde f}} \\ X }cco }$$

If the image $i(A) \subset X$ is a closed subset, then $i$ is called a closed Hurewicz cofibration.

Example

(retracts of relative cell complex inclusions are closed Hurewicz cofibrations)

If $A$ is a topological space and $i \colon A \hookrightarrow X$ is a relative cell complex inclusion, then $i$ is a closed Hurewicz cofibration (def. ).

Also every retract of such $i$ (this sense) is a closed Hurewicz cofibration.

Pushouts / space attachments

Cofiber sequences (below) are constructed by iterated pushouts in the category Top of topological spaces with continuous functions between them (space attachments), see at Top – Universal constructions.

Example

(quotient space by a subspace)

Let $X$ be a topological space and $A \subset X$ a non-empty subset. Consider the equivalence relation on $X$ which identifies all points in $A$ with each other. The resulting quotient space is denoted $X/A$.

Notice that $X/A$ is canonically a pointed topological space, with base point the equivalence class $A/A \subset X/A$ of $A$.

If $A = \emptyset$ is the empty space, then one defines

$$X/\emptyset \coloneqq X_+ \coloneqq X \sqcup \ast$$

to be the disjoint union space of $X$ with the point space. This is no longer a quotient space, but both constructions are unified by the pushout $i \colon A \to X$ along the map $A \to \ast$, equivalently the cokernel of the inclusion:

$$\array{ A &\overset{i}{\hookrightarrow}& X \\ \downarrow &(po)& \downarrow \\ \ast &\longrightarrow& X/A } \,.$$

Example

(union of two open or two closed subspaces is pushout)

Let $X$ be a topological space and let $A,B \subset X$ be subspaces such that

1. $A,B \subset X$ are both open subsets or are both closed subsets;

2. they constitute a cover: $X = A \cup B$

Write $i_A \colon A \to X$ and $i_B \colon B \to X$ for the corresponding inclusion continuous functions.

Then the commuting square

$$\array{ A \cap B &\longrightarrow& A \\ \downarrow &(po)& \downarrow^{\mathrlap{i_A}} \\ B &\underset{i_B}{\longrightarrow}& X }$$

is a pushout square in Top (see there).

By the universal property of the pushout this means in particular that for $Y$ any topological space then a function of underlying sets

$$f \;\colon\; X \longrightarrow Y$$

is a continuous function as soon as its two restrictions

$$f\vert_A \;\colon\; A \longrightarrow Y \phantom{AAAA} f\vert_A \;\colon\; B \longrightarrow Y$$

are continuous.

Proof

Clearly the underlying diagram of underlying sets is a pushout in Set. Therefore (by this prop.) we need to show that the topology on $X$ is the final topology induced by the set of functions $\{i_A, i_B\}$, hence that a subset $S \subset X$ is an open subset precisely if the pre-images (restrictions)

$$i_A^{-1}(S) = S \cap A \phantom{AAA} \text{and} \phantom{AAA} i_B^{-1}(S) = S \cap B$$

are open subsets of $A$ and $B$, respectively.

Now by definition of the subspace topology, if $S \subset X$ is open, then the intersections $A \cap S \subset A$ and $B \cap S \subset B$ are open in these subspaces.

Conversely, assume that $A \cap S \subset A$ and $B \cap S \subset B$ are open. We need to show that then $S \subset X$ is open.

Consider now first the case that $A;B \subset X$ are both open open. Then by the nature of the subspace topology, that $A \cap S$ is open in $A$ means that there is an open subset $S_A \subset X$ such that $A \cap S = A \cap S_A$. Since the intersection of two open subsets is open, this implies that $A \cap S_A$ and hence $A \cap S$ is open. Similarly $B \cap S$. Therefore

$$\begin{aligned} S & = S \cap X \\ & = S \cap (A \cup B) \\ & = (S \cap A) \cup (S \cap B) \end{aligned}$$

is the union of two open subsets and therefore open.

Now consider the case that $A,B \subset X$ are both closed subsets.

Again by the nature of the subspace topology, that $A \cap S \subset A$ and $B \cap S \subset B$ are open means that there exist open subsets $S_A, S_B \subset X$ such that $A \cap S = A \cap S_A$ and $B \cap S = B \cap S_B$. Since $A,B \subset X$ are closed by assumption, this means that $A \setminus S, B \setminus S \subset X$ are still closed, hence that $X \setminus (A \setminus S), X \setminus (B \setminus S) \subset X$ are open.

Now observe that (by de Morgan duality)

$$\begin{aligned} S & = X \setminus (X \setminus S) \\ & = X \setminus ( (A \cup B) \setminus S ) \\ & = X \setminus ( (A \setminus S) \cup (B \setminus S) ) \\ & = (X \setminus (A \setminus S)) \cap (X \setminus (B \setminus S)) \,. \end{aligned}$$

This exhibits $S$ as the intersection of two open subsets, hence as open.

A general abstract fact about pushouts which we will use repeatedly in the proofs below is the following:

Proposition

(pasting law)

Consider a diagram in Top (or in any other category) of the following form:

$$\array{ &\longrightarrow& &\longrightarrow& \\ \downarrow &(po)& \downarrow && \downarrow \\ &\longrightarrow& &\longrightarrow& } \,,$$

where the left square is a pushout.

Then: The total rectangle is a pushout precisely if the right square is.

We need the following two facts (prop. prop. ) regarding the stability of cofibrations under pushout.

Proposition

(pushout of cofibrations)

Let $A$ be a topological space and let $A \hookrightarrow X$ be a closed Hurewicz cofibration.

Then for every continuous function $f \colon A \to Y$, the pushout $f_\ast i$ in

$$\array{ A &\overset{f}{\longrightarrow}& Y \\ {}^{\mathllap{i}}\downarrow &(po)& \downarrow^{\mathrlap{f_\ast i}} \\ X &\longrightarrow& X \underset{A}{\sqcup} Y }$$

is also a closed Hurewicz cofibration. Moreover, if in addition

1. $i$ is a retract of a relative cell complex inclusion, then so is $f_\ast i$,

2. $i$ is a homotopy equivalence, then so is $f_\ast i$.

Prop. is a consequence of the existence of the Strøm model structure $Top_{Strom}$ and the classical model structure on topological spaces $Top_{Quillen}$ and of the fact that the identity functors $Top_{Strom} \underoverset{\underset{id}{\longrightarrow}}{\overset{id}{\longleftarrow}}{\bot} Top_{Quillen}$ constitute a Quillen adjunction.

Proposition

(quotient by contractible closed subspace)

Let $i \colon A \longrightarrow X$ be a closed Hurewicz cofibration.

If $f \colon A \to Y$ is a homotopy equivalence (def. ) then its pushout $i_\ast f$ in

$$\array{ A &\overset{i}{\longrightarrow}& X \\ {}^{\mathllap{f}}\downarrow &(po)& \downarrow^{\mathrlap{i_\ast(f)}} \\ Y &\longrightarrow& Y \underset{A}{\sqcup} X }$$

is also a homotopy equivalence.

In particular if $A$ is a contractible topological space (example ), then the coprojection

$$X \longrightarrow X/A$$

to the quotient space (example ) is a homotopy equivalence.

Prop. is again a consequence of the existence of the Strøm model structure $Top_{Strom}$: It is the statement that $Top_{Strom}$ is a left proper model category which follows (this cor.) since all its objects are evidently cofibrant. An elementary proof in point-set topology is offered in (Hatcher, prop. 0.17)

Mapping cones

Definition

(topological cylinder and cone)

Let $X$ be a topological space. Then

1. the standard cylinder on $X$ is the product topological space

   $$Cyl(X) \coloneqq X \times [0,1]$$

2. the standard cone on $X$ is the quotient space (example )

   $$Cone(X) \coloneqq Cyl(X) / (X \times \{0\})$$

   of the standard cylinder by the subspace $X \times \{0\} \subset X \times [0,1]$.

   Equivalently this is the following pushout in Top

   $$\array{ X \times \{0\} &\hookrightarrow& Cyl(X) \\ \downarrow &(po)& \downarrow \\ \ast &\longrightarrow& Cone(X) }$$

Lemma

Let $X$ be a topological space. Then the canonical inclusions

$$X \longrightarrow Cyl(X) \phantom{AAAA} \ast \longrightarrow Cone(X)$$

are homotopy equivalences. Hence every cone is a [contractible topological space]] (example ).

Definition

(mapping cylinder and mapping cone)

Let $f \colon X \to Y$ be a continuous function between topological spaces. Then

1. the mapping cylinder of $f$ is the space attachment

   $$Cyl(f) \coloneqq Y \cup_f Cyl(X)$$

   of $Y$ with the cylinder on $X$, according to def. , hence the following pushout in Top

   $$\array{ X &\overset{f}{\longrightarrow}& Y \\ \downarrow &(po)& \downarrow \\ Cyl(X) &\longrightarrow& Cyl(f) }$$

2. the mapping cone of $f$ is the space attachment

   $$Cone(f) \coloneqq Y \cup_f Cone(X)$$

   hence the following pushout in Top:

   $$\array{ X &\overset{f}{\longrightarrow}& Y \\ \downarrow &(po)& \downarrow \\ Cone(X) &\longrightarrow& Cone(f) }$$

Remark

In summary, def. and def. say that for $f \colon X \to Y$ a continuous function then we have a pasting of pushout diagrams in Top of the following form:

$$\array{ && X &\stackrel{f}{\to}& Y \\ && \downarrow^{\mathrlap{i_1}} &(po)& \downarrow \\ X &\stackrel{i_0}{\to}& Cyl(X) &\to & Cyl(f) \\ \downarrow &(po)& \downarrow &(po)& \downarrow \\ {*} &\to& Cone(X) &\to& Cone(f) } \,.$$

Since $X \to Cone(X)$ is a closed Hurewicz cofibration , the pasting law together with prop. therefore implies that also $Y \to Cone(f)$ is a closed Hurwicz cofibration.

Example

(suspension)

For $X$ a topological space, then the mapping cone (def. ) of the unique function $X \to \ast$ to the point space is

$$S X \coloneqq Cone(X \to \ast) \simeq Cone(X) \underset{X}{\sqcup} Cone(X) \,.$$

This is called the suspension of $X$.

The mapping cone of a map $X \to Y$ is to be thought of as the homotopy-quotient of the $Y$ by $X$, as opposed to be the naive quotient. This is made precise by the following two statements, lemma and lemma :

Lemma

If $f \colon X \to Y$ is a closed Hurewicz cofibration (def. ), then the coprojection

$$Cone(f) \longrightarrow Y/f(X)$$

from its mapping cone (def. ) to the naive quotient space (example ) is a homotopy equivalence.

Proof

Consider the diagram

$$\array{ X &\overset{f}{\longrightarrow}& Y \\ \downarrow &(po)& \downarrow \\ Cone(X) &\longrightarrow& Cone(f) \\ \downarrow &(po)& \downarrow \\ \ast &\longrightarrow& Cone(f)/Cone(X) }$$

Since $f$ is a closed Hurewicz cofibration, so is $Cone(X) \to Cone(f)$, by prop. . Since $Cone(X) \to \ast$ is a homotopy equivalence (lemma ), so is $Cone(f) \to Cone(f)/Cone(X)$, by prop. . But by lemma there is also a homeomorphism $Cone(f)/Cone(X) \simeq Y/f(X)$.

Lemma

Let $f \colon X \to Y$ be a continuous function such that the image $f(X) \subset Y$ is a closed subset.

Then there is a homeomorphism

$$Cone(f)/Cone(X) \simeq Y / f(X)$$

between the quotient space (example ) of the mapping cone of $f$ (def. ) by the cone of $X$ (def. ) and the quotient space of $Y$ be the image of $X$.

Proof

Consider the following diagram in Top:

$$\array{ f(X) &\longrightarrow& Y \\ \downarrow &(po)& \downarrow \\ f(Cone(X)) &\longrightarrow& Cone(f) \\ \downarrow &(po)& \downarrow \\ \ast &\longrightarrow& Cone(f)/Cone(X) }$$

Here the top square is a pushout by example , while the bottom square is a pushout by def. . Hence the total rectangle is also a pushout, by the pasting law (prop. ). But that total rectangle is the defining pushout for $Y/f(X)$ (by example ). Hence the statement follows by the universal property of the pushout.

Cofiber sequences

Proposition

Let $f \colon X \to Y$ be a continuous function with closed image $f(X) \subset Y$. Write $Cone(g)$ in

$$\array{ X &\overset{f}{\longrightarrow}& Y &\overset{g}{\longrightarrow}& Cone(f) &\overset{}{\longrightarrow}& Cone(g) }$$

for the mapping cone (spring) of the inclusion $g$ of $Y$ into the mapping cone of $f$.

Then the canonical quotient coprojection

$$Cone(g) \to \Sigma X$$

to the suspension of $X$ (example ) is a homotopy equivalence (def. ).

Proof

Since $g \colon Y \to Cone(f)$ is a closed Hurewicz cofibration (by remark ), lemma gives that

$$Cone(g) \to Cone(f)/g(Y)$$

is a homotopy equivalence. But then there is the following evident homeomorphism

$$Cone(f)/g(Y) = (Y \cup_f Cone(X))/Y \simeq Cone(X)/X \simeq S X \,.$$

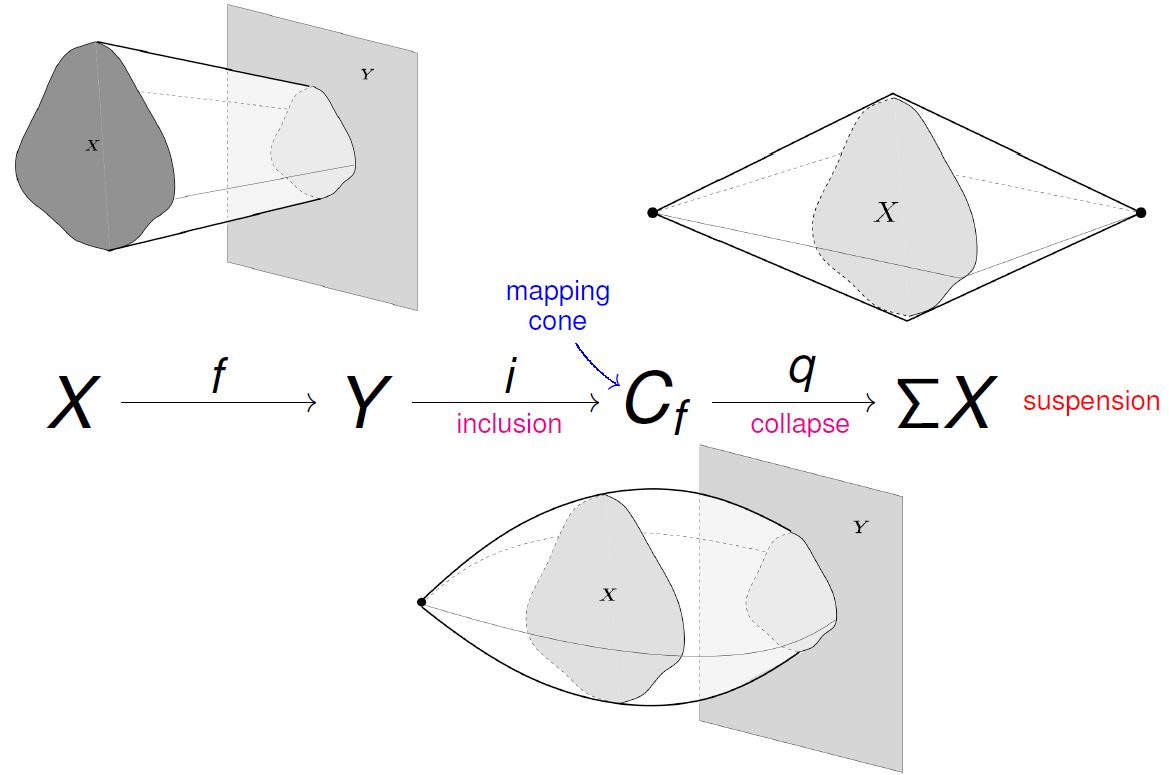
(graphics taken from Muro 10)

Hence from every $f \colon X \to Y$ with closed image, we get long sequences

$$\array{ X &\overset{f}{\longrightarrow}& Y &\overset{g}{\longrightarrow}& Cone(f) &\longrightarrow& Cone(g) \\ && && && \downarrow^{\mathrlap{\text{homotopy} \atop \text{equivalence}}} \\ && && && S X &\overset{S f}{\longrightarrow}& S Y &\longrightarrow& \cdots }$$

Pointed cofiber sequence

(…)