nLab tensor network

Idea

The term tensor network has become popular in quantum physics for essentially what in mathematical physics is known as Penrose notation and in monoidal category theory is referred to as string diagrams (see BCJ 10 for a bilingual account).

The term rose to prominence in quantum physics partly with discussion of finite quantum mechanics in terms of dagger-compact categories but mainly via its use for representing highly entangled states in the discussion of renormalization of non-perturbative effects in solid state physics (Swingle 09, Swingle 13) and the resulting discovery of the relation to holographic entanglement entropy and thus to the AdS/CFT correspondence.

In this context, a tensor network is a string diagram with an attitude, in that it is (just) a string diagram (typically regarded in the monoidal category of finite-dimensional vector spaces, but possibly also in super vector spaces etc.), but with:

1. the tensor product of all its external objects regarded as a space of states of a quantum system;

2. the element in that tensor product defined by the string diagram regarded as a state (wave function) of that quantum system.

For instance, if $\mathfrak{g}$ is a metric Lie algebra (with string diagram-notation as shown there), and with each tensor product-power of its dual vector space regarded as a Hilbert space, hence as a space of quantum states, via the given inner product on $\mathfrak{g}$, then an example of a tree tensor network state is the following:

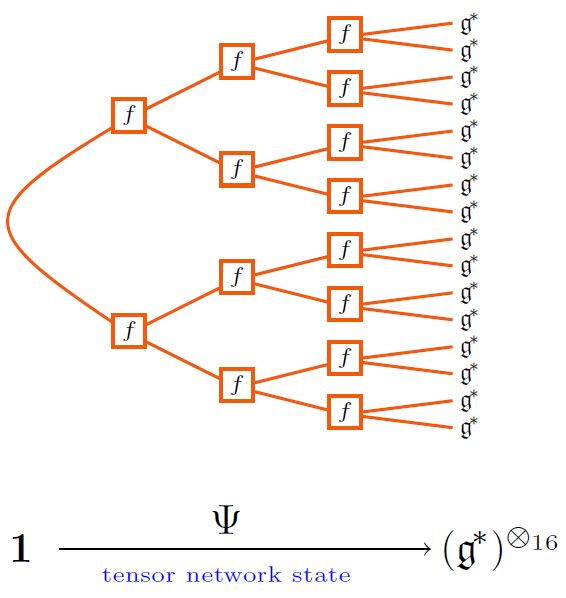
graphics from Sati-Schreiber 19c

The quantum states arising this way are generically highly entangled: roughly they are the more entangled the more vertices there are in the corresponding tensor network.

The following is an example of what is called a matrix product state:

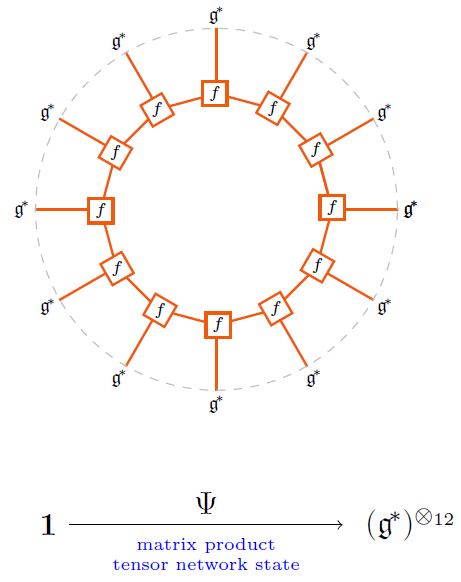
graphics from Sati-Schreiber 19c

The tree tensor network states in the form of Bruhat-Tits trees play a special role in the AdS/CFT correspondence, either as

1. a kind of lattice QFT-approximation to an actual boundary CFT quantum state,

2. as the p-adic geometric incarnation of anti de Sitter spacetime in the p-adic AdS/CFT correspondence,

3. as a reflection of actual crystal-site quantum states in AdS/CFT in solid state physics:

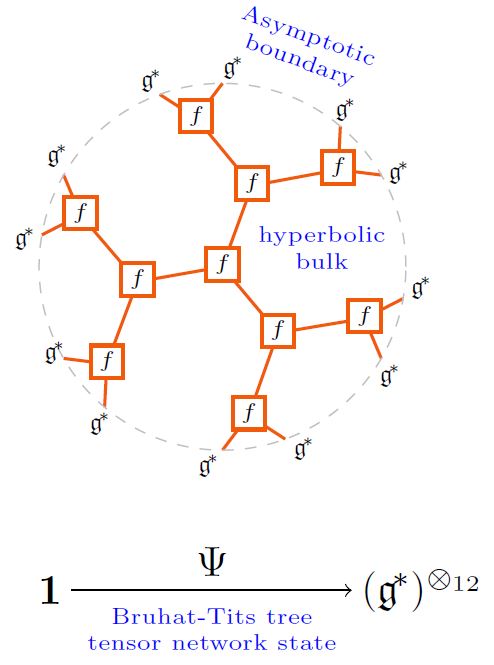
graphics from Sati-Schreiber 19c

(As in HMSS 16, HLM 19. But maybe one wants the Poincaré-dual networks, instead, as in HMPS 18?)

For tensor network states dual to tesselations of hyperbolic space and made from perfect tensors one finds that the entanglement entropy of the tensor subspace associated with an interval on the boundary becomes proportional, for large number of vertices, to the hyperbolic bulk boundary length of the segment of the tree network that ends on this interval, according to the Ryu-Takayanagi formula (PYHP 15, Theorem 2). Hence one speaks of holographic entanglement entropy. For more on this see below.

General tensor network states are mixtures of the above examples. For instance in … is the suggestion that BTZ black holes are encoded by networks that look like Bruhat-Tits trees towards the boundaries and like matrix product states towards the interior:

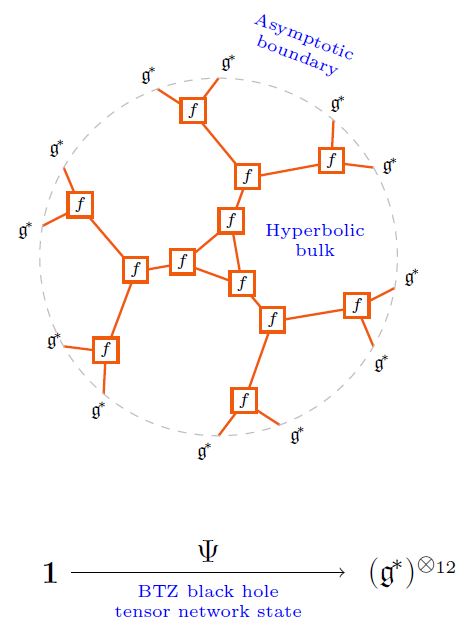
(As in ESZ 19.)

For holographic entanglement entropy

under construction

Appearance in renormalization:

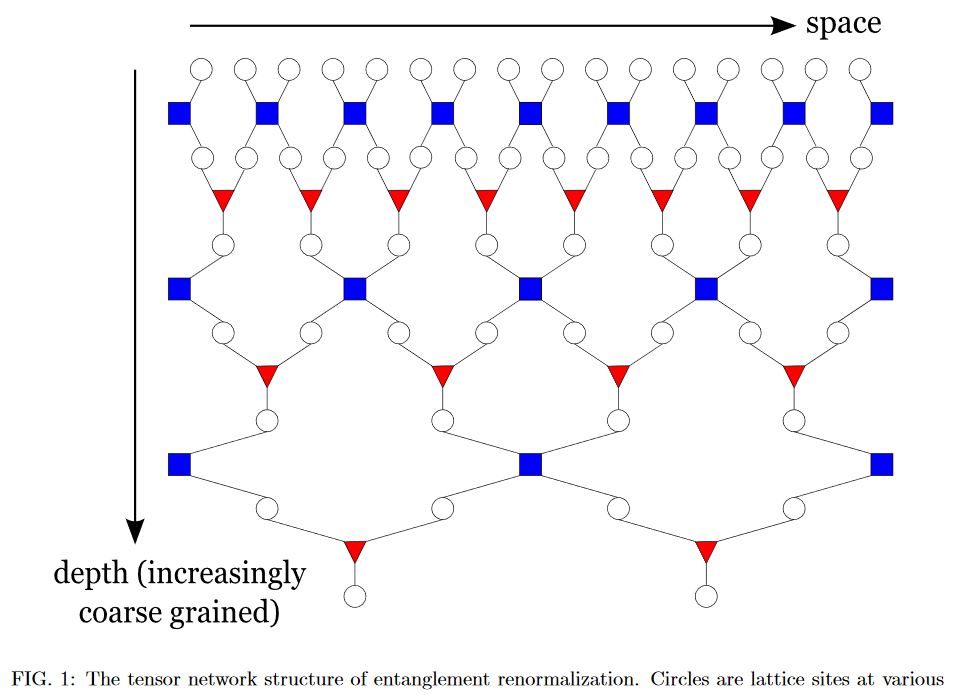
from Swingle 09

Application to holographic entanglement entropy (…)

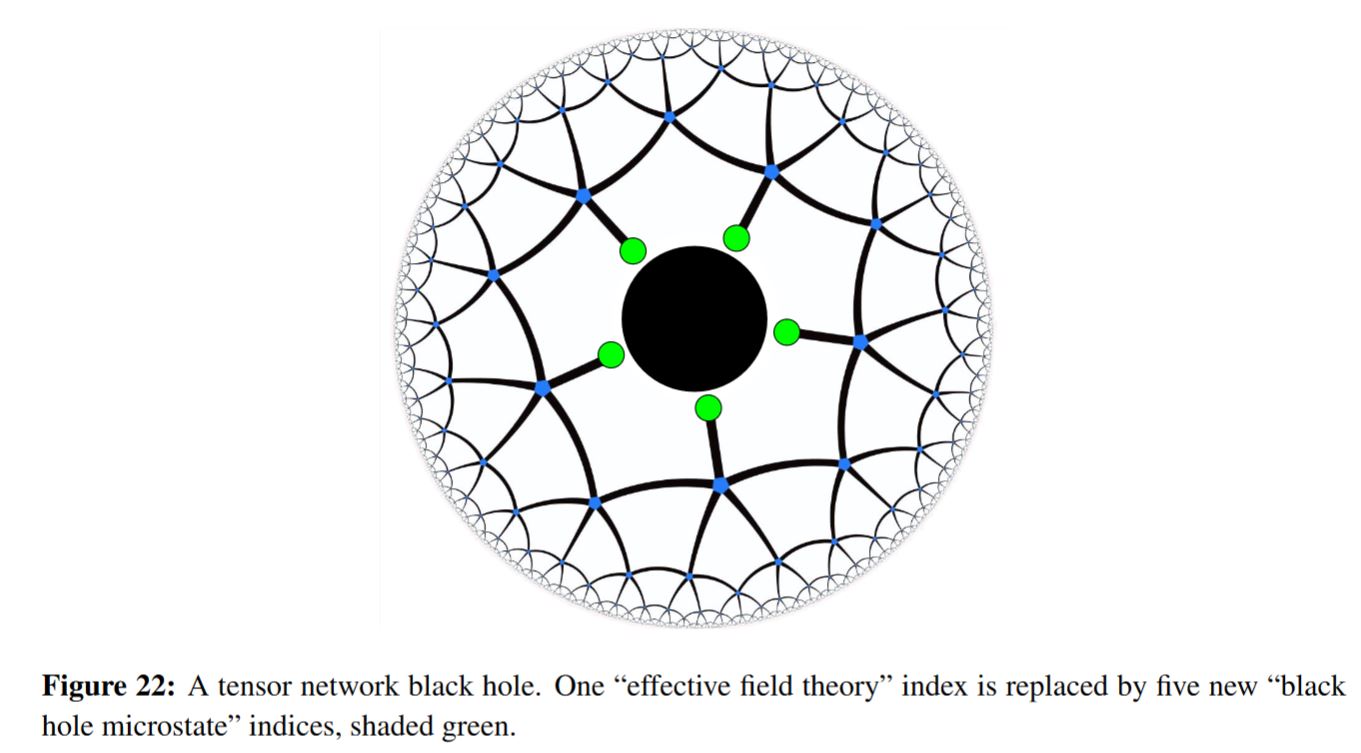
graphics grabbed from Harlow 18, see at HaPPY code

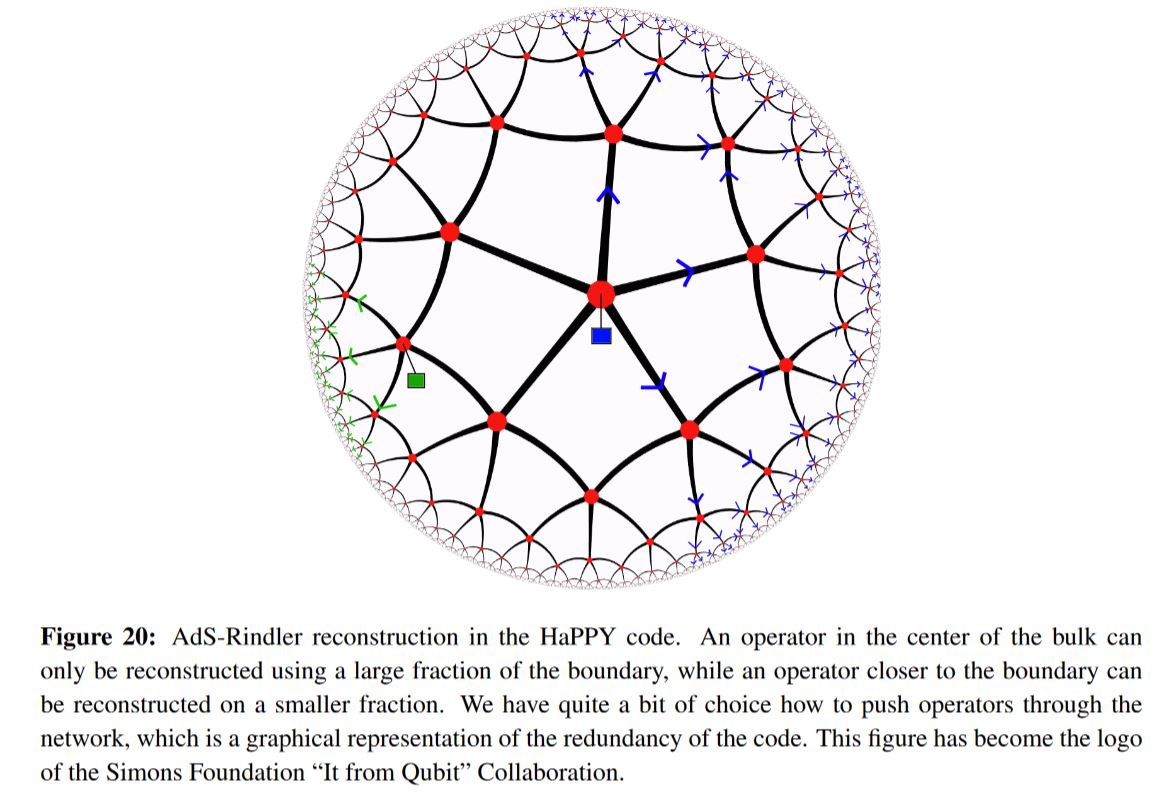
graphics grabbed from Harlow 18, see at HaPPY code

In this context the Ryu-Takayanagi formula for holographic entanglement entropy has an exact proof PYHP 15, Theorem 2.

Examples

• matrix product state

• tree tensor network state

• MERA state?

Related concepts

• string diagram/Penrose notation

• finite quantum mechanics in terms of dagger-compact categories

• quantum many-body physics, condensed matter physics

• quantum computing, quantum information theory

  quantum error correction

• tensor, tensor product, tensor category

• neural network

quantum probability theory – observables and states

• states

  • classical state

  • quantum state

    • space of states (in geometric quantization)

    • state on a star-algebra, quasi-state

    • qbit, Bell state

      dimer, tensor network state

    • quantum state preparation

    • probability amplitude, quantum fluctuation

    • pure state

      • wave function

      • bra-ket

      • Bell state

    • quantum superposition, quantum interference

    • quantum entanglement

    • quantum measurement

      Born rule

      wave function collapse

      measurement problem

    • superselection sector

    • mixed state, density matrix

      entanglement entropy

      holographic entanglement entropy

    • coherent quantum state

  • ground state, excited state

  • quasi-free state

  • Fock space, second quantization

  • vacuum, vacuum state

    • Hadamard state

    • vacuum diagram

    • vacuum expectation value, vacuum amplitude, vacuum fluctuation

    • vacuum energy

    • vacuum polarization

    • interacting vacuum

    • thermal vacuum, KMS state

    • vacuum stability

      • false vacuum, tachyon, Coleman-De Luccia instanton

    • theta vacuum

    • perturbative string theory vacuum

      • non-geometric string theory vacuum

      • landscape of string theory vacua

  • entangled state

  • tensor network state

    • matrix product state

    • tree tensor network state

• observables

  • quantum observable, beable

  • algebra of observables, star-algebra

  • Bohr topos

  • quantum operator (in geometric quantization)

  • quantum operation, quantum effect, effect algebra

  • in quantum field theory

    • local observable

    • polynomial observable

      • linear observable

        • field observable

    • regular observable

    • microcausal observable

    • normal-ordered product, time-ordered products, retarded product

    • Wick algebra

    • scattering amplitude

    • interacting field algebra of observables, Bogoliubov's formula

• GNS construction

• theorems

  • order-theoretic structure in quantum mechanics

    • Gleason's theorem

    • Alfsen-Shultz theorem

    • Harding-Döring-Hamhalter theorem

    • Kochen-Specker theorem

    • Nuiten's lemma

  • Wigner's theorem

  • no-cloning theorem

  • Bell's theorem

References

General

Review and exposition:

• Jacob Biamonte, Stephen R. Clark, Dieter Jaksch, Categorical Tensor Network States, AIP Advances 1(4), 042172 (2011) (arXiv:1012.0531)

• Roman Orus, A Practical Introduction to Tensor Networks: Matrix Product States and Projected Entangled Pair States, Annals of Physics 349 (2014) 117-158 (arXiv:1306.2164)

• Jens Eisert, Entanglement and tensor network states, Modeling and Simulation 3, 520 (2013) (arXiv:1308.3318)

• Jacob Biamonte, Ville Bergholm, Tensor Networks in a Nutshell, Contemporary Physics (arxiv:1708.00006)

• Bei Zeng, Xie Chen, Duan-Lu Zhou, Xiao-Gang Wen:

  Part IV of: Quantum Information Meets Quantum Matter – From Quantum Entanglement to Topological Phases of Many-Body Systems, Quantum Science and Technology (QST), Springer (2019) $[$arXiv:1508.02595, doi:10.1007/978-1-4939-9084-9$]$

• Roman Orus, Tensor networks for complex quantum systems, Nature Reviews Physics 1, 538-550 (2019) (arXiv:1812.04011, doi:10.1038/s42254-019-0086-7)

• Jacob Biamonte, Lectures on Quantum Tensor Networks (arXiv:1912.10049)

• Shi-Ju Ran, Emanuele Tirrito, Cheng Peng, Xi Chen, Luca Tagliacozzo, Gang Su, Maciej Lewenstein, Tensor Network Contractions – Methods and Applications to Quantum Many-Body Systems, Lecture Notes in Physics, Springer (2020) (arXiv:1708.09213, doi:10.1007/978-3-030-34489-4)

With global symmetry:

• Sukhwinder Singh, Robert N. C. Pfeifer, Guifre Vidal, Tensor network decompositions in the presence of a global symmetry, Phys. Rev. A82:050301, 2010 (arXiv:0907.2994)

• Sukhwinder Singh, Robert N. C. Pfeifer, Guifre Vidal, Tensor network states and algorithms in the presence of a global $U(1)$ symmetry, Phys. Rev. B 83, 115125 (2011) (arXix:1008.4774)

• Sukhwinder Singh, Guifre Vidal, Tensor network states and algorithms in the presence of a global $SU(2)$ symmetry, Phys. Rev. B 86, 195114 (2012) (arXiv:1208.3919)

Further resources:

• Tensor Network Initiative

• tensornetwork.org

Application in solid state physics

Discussion of solid state physics via tensor network states:

General:

• Jens Eisert, M. Cramer, M.B. Plenio, Area laws for the entanglement entropy - a review, Rev. Mod. Phys. 82, 277 (2010) (arXiv:0808.3773)

• Roman Orus, A Practical Introduction to Tensor Networks: Matrix Product States and Projected Entangled Pair States, Annals of Physics 349 (2014) 117-158 (arXiv:1306.2164)

• Jens Eisert, Entanglement and tensor network states, Modeling and Simulation 3, 520 (2013) (arXiv:1308.3318)

• Thorsten B. Wahl, Tensor network states for the description of quantum many-body systems (arXiv:1509.05984)

• Kouichi Okunishi, Tomotoshi Nishino, Hiroshi Ueda, Developments in the Tensor Network – from Statistical Mechanics to Quantum Entanglement (arXiv:2111.12223)

Concrete materials:

• A. Kshetrimayum, C. Balz, B. Lake, Jens Eisert, Tensor network investigation of the double layer Kagome compound $Ca_{10} Cr_{7} O_{28}$ (arXiv:1904.00028)

Classification of (topological) phases of matter via tensor network states:

• C. Wille, O. Buerschaper, Jens Eisert, Fermionic topological quantum states as tensor networks, Phys. Rev. B 95, 245127 (2017) (arXiv:1609.02574)

• Andreas Bauer, Jens Eisert, Carolin Wille, Towards a mathematical formalism for classifying phases of matter (arXiv:1903.05413)

Tensor networks for string-net models for topological order:

On string-net models via tensor networks:

• O. Buerschaper, M. Aguado, G. Vidal, Explicit tensor network representation for the ground states of string-net models, Phys. Rev. B 79 (2009) 085119 $[$arXiv:0809.2393, doi:10.1103/PhysRevB.95.195110$]$

• Zheng-Cheng Gu, Michael Levin, Brian Swingle, Xiao-Gang Wen, Tensor-product representations for string-net condensed states, Phys. Rev. B 79 (2009) 085118 $[$doi:10.1103/PhysRevB.79.085118$]$

In holographic entanglement entropy

The use of tensor networks as a tool in holographic entanglement entropy goes back to

• Brian Swingle, Entanglement Renormalization and Holography, Phys. Rev. D 86, 065007 (2012) (arXiv:0905.1317)

• Brian Swingle, Constructing holographic spacetimes using entanglement renormalization (arXiv:1209.3304, spire:1185813)

Review in

• Frank Verstraete, J. I. Cirac, V. Murg, Matrix Product States, Projected Entangled Pair States, and variational renormalization group methods for quantum spin systems, Adv. Phys. 57,143 (2008) (arXiv:0907.2796)

In the $p$-adic AdS/CFT correspondence

Tensor networks associated with Bruhat-Tits trees in p-adic AdS/CFT correspondence:

• Matthew Heydeman, Matilde Marcolli, Ingmar Saberi, Bogdan Stoica, Tensor networks, $p$-adic fields, and algebraic curves: arithmetic and the $AdS_3/CFT_2$ correspondence (arXiv:1605.07639)

• Arpan Bhattacharyya, Ling-Yan Hung, Yang Lei, Wei Li, Tensor network and ($p$-adic) AdS/CFT, JHEP 1801 (2018) 139 (arXiv:1703.05445)

• Ling-Yan Hung, Wei Li, Charles M. Melby-Thompson, $p$-adic CFT is a holographic tensor network (arXiv:1902.01411)

• Lin Chen, Xirong Liu, Ling-Yan Hung, Emergent Einstein Equation in p-adic CFT Tensor Networks (arXiv:2102.12022)

• Lin Chen, Xirong Liu, Ling-Yan Hung, Bending the Bruhat-Tits Tree I:Tensor Network and Emergent Einstein Equations (arXiv:2102.12023)

• Lin Chen, Xirong Liu, Ling-Yan Hung, Bending the Bruhat-Tits Tree II: the p-adic BTZ Black hole and Local Diffeomorephism on the Bruhat-Tits Tree (arXiv:2102.12024)

Discussion of BTZ black holes via tensor networks in the p-adic AdS/CFT correspondence:

• Matthew Heydeman, Matilde Marcolli, Sarthak Parikh, Ingmar Saberi, Nonarchimedean Holographic Entropy from Networks of Perfect Tensors (arXiv:1812.04057)

See also

• Alexander Jahn, Zoltán Zimborás, Jens Eisert, Central charges of aperiodic holographic tensor network models (arXiv:1911.03485)

  (quasicrystal boundary states)

• Alexander Jahn, Zoltán Zimborás, Jens Eisert, Tensor network models of AdS/qCFT (arXiv:2004.04173)

In quantum computation

In quantum computation:

• Isaac H. Kim, Brian Swingle, Robust entanglement renormalization on a noisy quantum computer (arXiv:1711.07500)

  (specifically for classically controlled quantum computation in terms of holographic tensor network states)

As quantum error correcting codes

Further interpretation of tensor networks in terms of quantum error correcting codes:

• Andrew J. Ferris, David Poulin, Tensor Networks and Quantum Error Correction, Phys. Rev. Lett. 113, 030501 (2014) (arXiv:1312.4578)

and specifically in the HaPPY code modelling holographic entanglement entropy:

• Ahmed Almheiri, Xi Dong, Daniel Harlow, Bulk Locality and Quantum Error Correction in AdS/CFT, JHEP 1504:163,2015 (arXiv:1411.7041)

• Fernando Pastawski, Beni Yoshida, Daniel Harlow, John Preskill, Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149 (arXiv:1503.06237)

reviewed in

• Daniel Harlow, TASI Lectures on the Emergence of Bulk Physics in AdS/CFT (arXiv:1802.01040)

Generalization to the Majorana dimer code:

• Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting codes, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)

reviewed in:

• Alexander Jahn, Jens Eisert, Holographic tensor network models and quantum error correction: A topical review (arXiv:2102.02619)

Discussion of asymptotic boundaries of hyperbolic tensor networks as quasicrystals:

• Latham Boyle, Madeline Dickens, Felix Flicker, Conformal Quasicrystals and Holography, Phys. Rev. X 10, 011009 (2020) (arXiv:1805.02665)

See also

• Ning Bao, Geoffrey Penington, Jonathan Sorce, Aron C. Wall, Beyond Toy Models: Distilling Tensor Networks in Full AdS/CFT (arXiv:1812.01171)

• Ning Bao, Geoffrey Penington, Jonathan Sorce, Aron C. Wall, Holographic Tensor Networks in Full AdS/CFT (arXiv:1902.10157)

• Alexander Jahn, Marek Gluza, Fernando Pastawski, [[Jens Eisert?, Majorana dimers and holographic quantum error-correcting codes (arXiv:1905.03268)

Relation to spin chains

Relation to spin chains:

• Mari Carmen Banuls, Michal P. Heller, Karl Jansen, Johannes Knaute, Viktor Svensson, From spin chains to real-time thermal field theory using tensor networks (arXiv:1912.08836)

Application to lattice gauge theory

Application to lattice gauge theory:

• Luca Tagliacozzo, Alessio Celi, Maciej Lewenstein, Tensor Networks for Lattice Gauge Theories with continuous groups, Phys. Rev. X 4, 041024 (2014) (arXiv:1405.4811)

• M.C. Bañuls, R. Blatt, J. Catani, A. Celi, J.I. Cirac, M. Dalmonte, L. Fallani, K. Jansen, M. Lewenstein, S. Montangero, C.A. Muschik, B. Reznik, E. Rico, Luca Tagliacozzo, K. Van Acoleyen, Frank Verstraete, U.-J. Wiese, M. Wingate, J. Zakrzewski, P. Zoller:

  Simulating Lattice Gauge Theories within Quantum Technologies

  (arXiv:1911.00003)

In higher parallel transport

Discussion in relation to higher parallel transport:

• Arthur Parzygnat, Two-dimensional algebra in lattice gauge theory, Journal of Mathematical Physics 60, 043506 (2019) (arXiv:1802.01139, doi:10.1063/1.5078532)

Related to language models

• Vasily Pestun, Yiannis Vlassopoulos, Tensor network language model, arXiv:1710.10248