nLab traced monoidal category
Context
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
-
monoidal dagger-category?
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Contents
Idea
The concept of traced monoidal category axiomatizes the structure on a monoidal category for it to have a sensible notion of (partial) trace the way it exists canonically in compact closed categories. Traced monoidal categories sometimes only have right or left traces, and are referred to as right traced or left traced respectively. A category with compatible right and left traces is called a planar traced category. If the right and left traces agree, then we call a planar traced category spherical.
Graphically, the trace of an endomorphism is represented by the closed loop
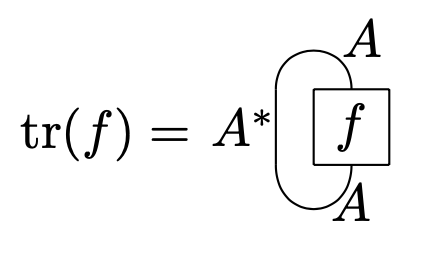
The ambiguity in whether to close the loop to the right or to the left is codified in the difference between left and right traced categories. Every pivotal category can be canonically made into a planar traced category by using its implicit distinguished morphisms to close loops. Pivotal categories which induce spherical traced structures are known as spherical categories. In this way, traced monoidal categories generalize the trace operation to categories which do not necessarily have duals.
In denotational semantics of programming languages, the trace is used to model recursion, though if the language is not substructural?, then this can be simplified to a fixed point operator.
Definition
The original definition due to (Joyal-Street-Verity 96) is stated in the setting of balanced monoidal categories. Here we present a very general formulation, as given in Selinger’s survey.
A monoidal category is said to be right traced if it is equipped with family of operations
for all , satisfying the following four axioms:
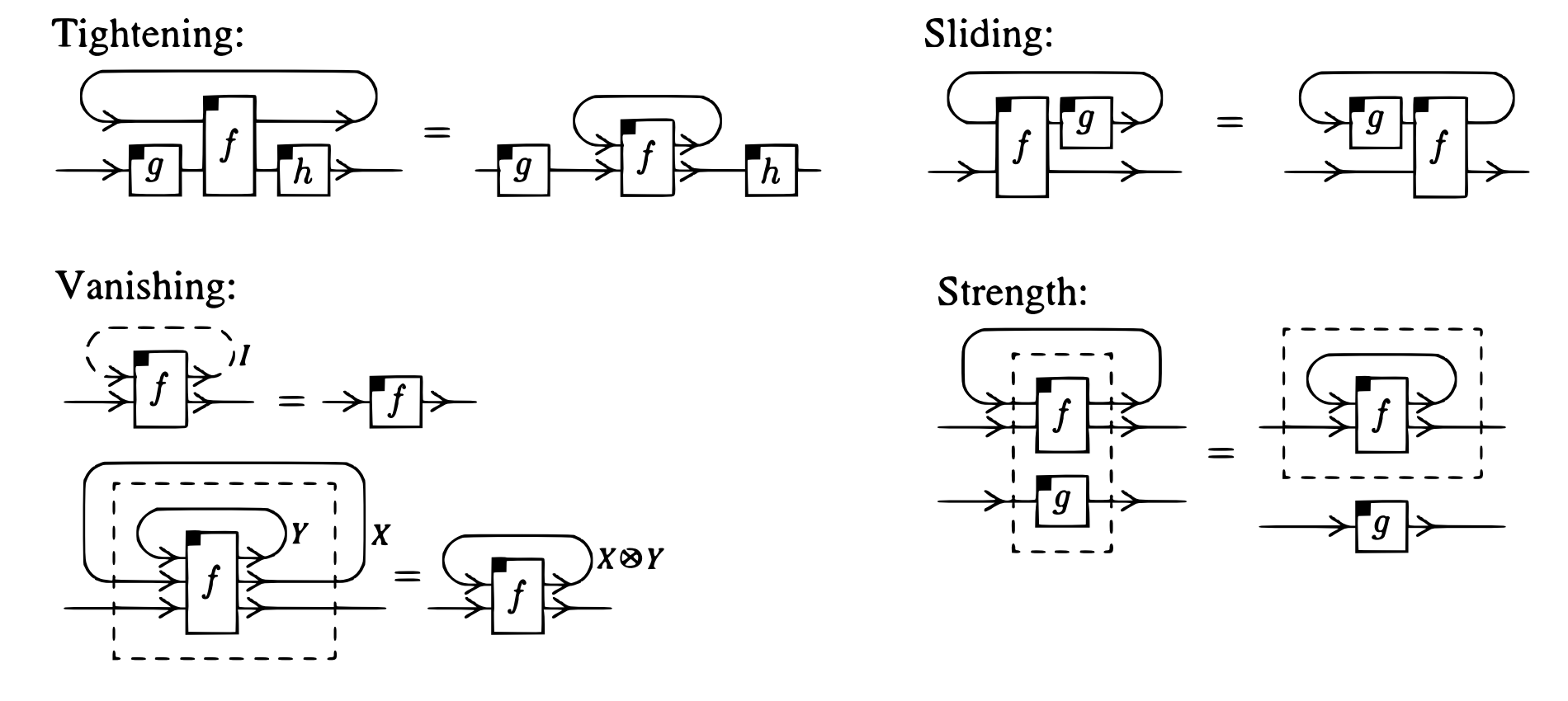
- Tightening (naturality in ) For all , , ,
- Sliding (naturality in ) for all , ,
- Vanishing For all ,
and
for all .
- Strength For all , ,
Graphically, we fix the notation for right trace
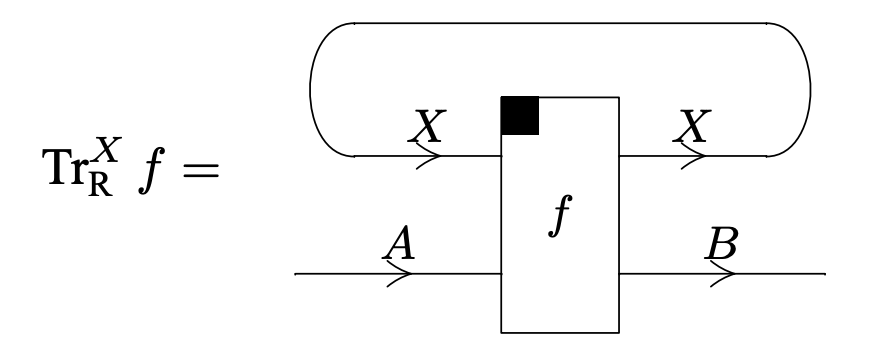
The above axioms are described with the following pictures:
In the presence of a braiding (such as in a symmetric monoidal category), we additionally require a yanking axioms:
- Yanking: for all
where is the briading.
A left traced category is defined similarly, with a family of morphisms
satisfying symmetric axioms. We write the left trace graphically as
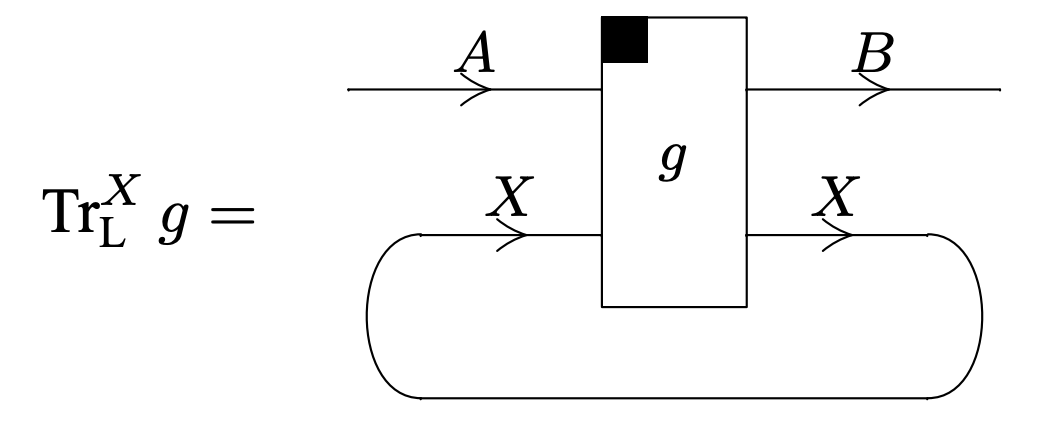
A planar traced category is a monoidal category which is simultaneously left and right traced, such that the following axioms are satisfied:
- Interchange For all ,
- Left pivoting For all ,
- Right pivoting For all ,
Graphically, these axioms can be stated as below:
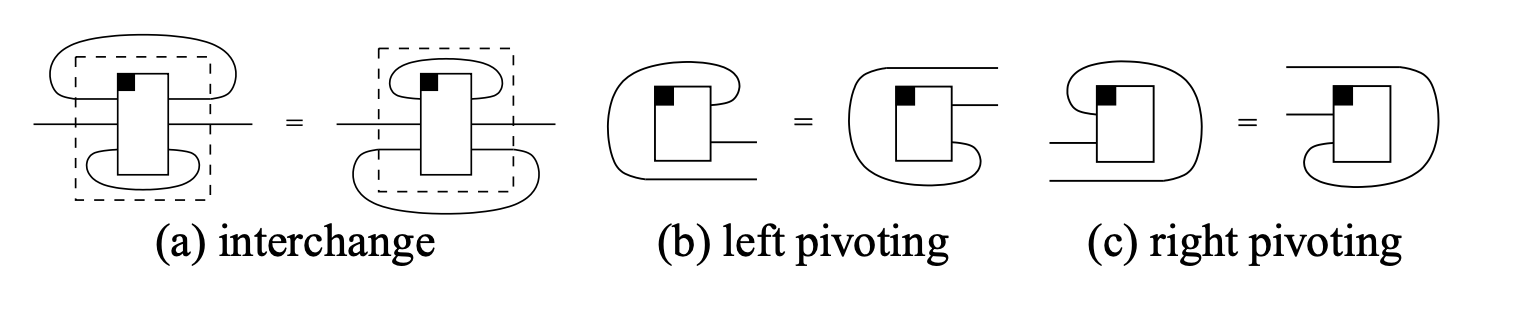
It is from these axioms that pivotal categories get their name.
A spherical trace category is a planar traced category in which the left and right partial traces agree. That is, for any endomorphism in we have that
Examples
-
The category of finite-dimensional vector spaces is traced monoidal. In skeletal form, the objects are natural numbers regarded as dimensions, morphisms are matrices regarded as linear maps, and tensor product is multiplication of the dimensions. The trace is a minor generalization of matrix trace:
This is an instance of a trace in a compact closed category.
-
The category of profunctors is also compact closed, hence traced monoidal (actually a bicategory, though). The trace of a profunctor is the profunctor given by the coend formula:
-
The category of sets and partial functions with the coproduct monoidal structure is traced, if we let the trace of a partial function be defined as follows. First, let , and so on be the evident partial functions that come from restricting the domain and codomain of . Then define
if either or if there exists such that . See for instance Section 5.2 of (Abramsky, Haghverdi and Scott). This is an example of a partially additive category.
This is a basis for a categorical semantics of “while loops” in programming languages: we keep applying while it is returning in .
-
Consider the category of pointed cpo‘s and continuous functions. A pointed cpo is a poset with a bottom element and least upper bounds of -chains. The morphisms preserve least upper bounds of chains but are not required to preserve bottom elements. This is a cartesian monoidal category, and with this structure it is traced, if we let the trace of a continuous function be given as follows. First, for fixed , let be the least fixed point of , writing for the second product projection. Here the least fixed point exists by Tarski’s fixed point theorem, indeed
Then we let
In Haskell notation, where ‘let’ allows recursive definitions, we can more swiftly just write
(except that the built-in product types in Haskell are lifted products rather than categorical products: in Haskell is like but with an extra bottom element added).
This is an example of a cartesian category with a parameterized fixed point operator (Hasegawa 1997).
Properties
Relation to compact closed categories
Every compact closed category is equipped with a canonical trace defined by
where is a unit and is a counit of appropriate adjunctions (note that the symmetry makes the dual both a right and left adjoint of : the adjunctions are ambidextrous).
Conversely, given a traced monoidal category , there is a free construction completion of it to a compact closed category (Joyal-Street-Verity 96):
the objects of are pairs of objects of , a morphism in is given by a morphism of the form in , and composition of two such morphisms and is given by tracing out from the composite
Note that embeds fully-faithfully in by sending to , where is the unit object of the monoidal structure.
Furthermore, a traced monoidal category that is -autonomous must already be compact closed; see HH13.
In cartesian monoidal categories
For a cartesian monoidal category, the existence of a trace operator is equivalent to the existence of a “parameterized” fixed point operator satisfying certain properties (Hasegawa 1997). When the category is a Lawvere theory, this is related to the notion of iteration theory.
Adding traces
Since any full monoidal subcategory of a traced monoidal category inherits a trace, not every monoidal category can be fully embedded into a traced monoidal category, and hence also not into a compact closed category. In fact, Plotkin observed that there are monoidal categories that cannot even be faithfully mapped into a traced monoidal category. This can be seen from the fact that a traced monoidal category has the “cancellation property” that if then (since the latter is a trace of the former with one of the copies of transposed), but not all monoidal categories have this property.
Relation to feedback categories
Feedback categories?KSW02 are a weakening of the axioms of traced monoidal categories. Feedback categories do not satisfy the yanking axiom and they only satisfy a weaker form of naturality on the object to be traced. Examples include some categories of automata.
Categorical semantics
Traced monoidal categories serve as an “operational” categorical semantics for linear logic, known as Geometry of Interactions. See there for more.
In this context the free compact closure from above is sometimes called the Geometry of Interaction construction and denoted (Abramsky-Haghverdi-Scott 02, def. 2.6).
References
The concept was introduced in
- André Joyal, Ross Street, Dominic Verity, Traced monoidal categories, Math. Proc. Camb. Phil. Soc. 119 (1996) 447-468 [pdf, doi:10.1017/S0305004100074338]
A good exposition is found in
- Peter Selinger, A survey of graphical languages for monoidal categories, New structures for physics (pdf)
A characterization of trace structures on cartesian monoidal categories is given in
- Masahito Hasegawa, Recursion from Cyclic Sharing: Traced Monoidal Categories and Models of Cyclic Lambda Calculi, Proc. 3rd International Conference on Typed Lambda Calculi and Applications (TLCA 1997). Springer LNCS1210, 1997 (citeseer)
The equivalence between traces and parameterized fixed point operators appears as Theorem 3.1 (the author notes that this theorem was also proved independently by Martin Hyland).
Comprehensive discussion as a source for categorical semantics of the Geometry of Interactions is in
- Samson Abramsky, Esfandir Haghverdi, Philip Scott, Geometry of Interaction and Linear Combinatory Algebras. MSCS, vol. 12(5), 2002, 625-665, CUP (2002) (citeseer)
The combination with star-autonomous structure was discussed in
- Tamás Hajgató and Masahito Hasegawa, Traced -autonomous categories are compact closed, TAC, 2013
Feedback categories and their connection to traced monoidal categories were discussed in
- Piergiulio Katis, Nicoletta Sabadini, Bob Walters. Feedback, trace and fixed-point semantics, 2002 (Numdam).
Last revised on September 15, 2023 at 15:49:12. See the history of this page for a list of all contributions to it.