nLab Haldane model

For the Haldane phase see instead at Heisenberg model.

---

Idea

In solid state physics, the Haldane model is a model for effectively 2-dimensional crystalline Chern insulators (ie. topological phases of matter “without symmetry protection”) obtained by starting with a simple model for a graphene-like 2d semi-metal and then adding a mass term and interactions (similar to spin-orbit coupling) which break the time-reversal symmetry and the spatial inversion symmetry.

Definition

Consider the honeycomb crystal lattice and consider the following three lattice sites $a_i \in \mathbb{R}^2$:

(from DTC)

The graphene-like semi-metal model

The Hilbert space of quantum states of the Haldane model is the direct sum of copies of $\mathbb{C}^2$ (regarded as the defining/fundamental representation of SU(2)) indexed by the sites in a Brillouin zone of this hexagonal lattice.

The un-deformed Bloch-Hamiltonian at momentum/wave vector $k$ in the Brillouin torus $\widehat{\mathbb{T}}^2$ is

(1)$$H_0(k) \;\coloneqq\; t_1 \cdot \underoverset{i = 1}{3}{\sum} \; \big( cos(k \cdot a_i) \sigma_x - \sigma_y sin(k \cdot a_i) \big) \,,$$

where

1. $t_1 \in \mathbb{R}$ is some real parameter,

2. the sum ranges over the three unit cell sites shown above,

3. $k \cdot a_i$ denotes the canonical inner product (evaluation pairing) of the wave vector with a position space lattice vector,

4. $\sigma_x, \sigma_y, \sigma_z$ are the Pauli matrices acting as linear operators of the on-site copies of the SU(2)-representation $\mathbb{C}^2$.

This undeformed Hamiltonian (1) is a simple but good model for the electronic band structure of a graphene-like 2-dimensional semi-metal.

Deformation by the Haldane mass term

Consider now also the following next-to-mearest neighbour site vectors $b_i \in \mathbb{R}^2$ in the above honeycomb lattice:

(from DTC)

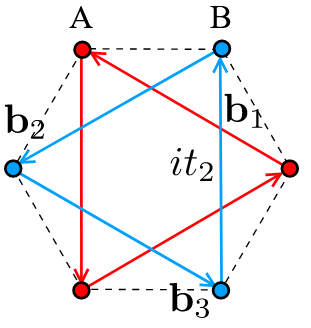
The full Bloch-Hamiltonian of the Haldane model is the deformation of $H_0(k)$ (1) by a mass term of the following form:

(2)$$H(k) \;\coloneqq\; H_0(k) \;+\; \underset{ \mathrm{mass}\;\mathrm{term} }{ \underbrace{ \left( M \;+\; 2 t_2 \underoverset{j = 1}{3}{\sum} sin(k \cdot b_i) \right) \cdot \sigma_z } } \,,$$

where

1. $t_2 \in \mathbb{R}$ is a second real parameter

2. the sum is now over the above three next-to-nearest neighbour site vectors $b_i$.

Notice that (only) for $t_2 = 0$ this reduces to the deformation by a constant mass term (which is often understood as the default meaning of “mass term”):

(3)$$H(k)_{t_2 = 0} \;=\; t_1 \cdot \underoverset{i = 1}{3}{\sum} \; \big( cos(k \cdot a_i) \sigma_x - \sigma_y sin(k \cdot a_i) \big) \;+\; \underset{ \mathclap{ \mathrm{constant}\;\mathrm{mass}\;\mathrm{term} } }{ \underbrace{ M \sigma_z } } \,,$$

Properties

Phase diagram

First of all, the Haldane model

• at M = 0 constitutes a non-trivial graphene-like topological semi-metal-phase with two Dirac points.

(graphics from SS 22)

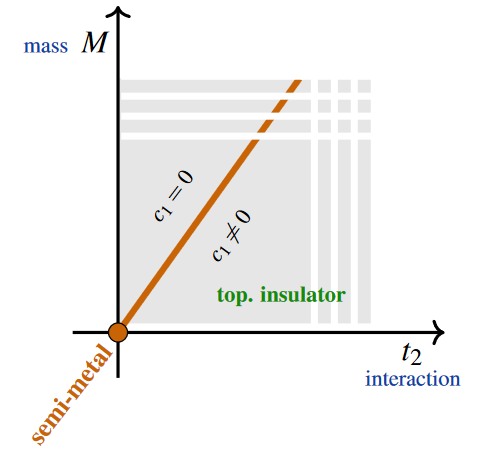
For $M \neq 0$ and as the parameter $t_2$ (2) increases, the Haldane model passes, consecutively, through

1. at $0 \leq t_2/M \lt \frac{1}{3 \sqrt{3}}$ – in particular where the mass term is constant (3) at $t_2 = 0$ –, a topologically trivial insulator-phase with Berry curvature concentrated (see below) around the would-be Dirac points of the graphene-like semi-metal phase which has been gapped out by the constant mass term;

2. at $t_2/M = \frac{1}{3 \sqrt{3}} \sim 0.19$ a non-trivial topological semi-metal-phase with a single band node;

3. at $\frac{1}{3\sqrt{3}} \lt t_2/M$ a non-trivial topological insulator-phase.

   This is the non-trivial Chern insulator-phase of the Haldane model.

Berry curvature

A curious property of the Haldane model, possibly not shared by all 2d Chern insulators, is that its Berry curvature is strongly localized around the (would-be) nodal Dirac points, hence that the Berry connection is essentially a flat connection on the complement of a small neighbourhood retract of the (would-be) nodal points.

(eg. Atteia 16, Sec. 2-3.4, p. 4, DTC here)

(from Atteia 16, Fig. 2.7)

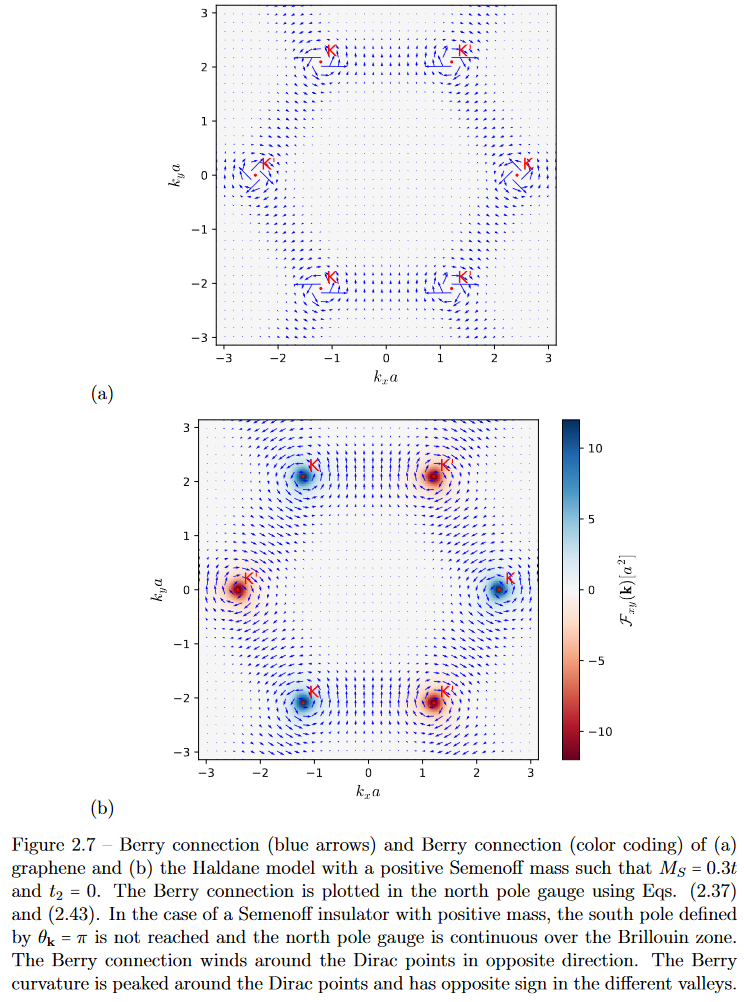
Concretely, the above graphics shows the Berry curvature in the Haldane model for constant mass term, hence in the case that the interaction paramater $t_2$ (2) vanishes:

(from DTC)

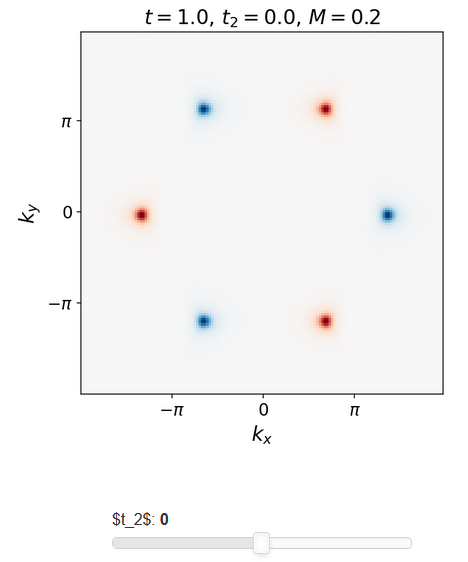
Since blue and red coloring denotes Berry curvature of opposite sign, the figure makes it plausibly manifest that the integrated Berry curvature – and thus the first Chern number of the valence bundle – vanishes for $M \neq 0$, $t_2 = 0$. This is the statement that the Chern insulator-phase of the Haldane model at $t_2 = 0$ is topologically trivial.

In constract, as $t_2/M \gt \frac{1}{3 \sqrt{3}}$, the Berry curvature is still concentrated around the would-be Dirac points, but now it has the same sign everywhere:

(from DTC)

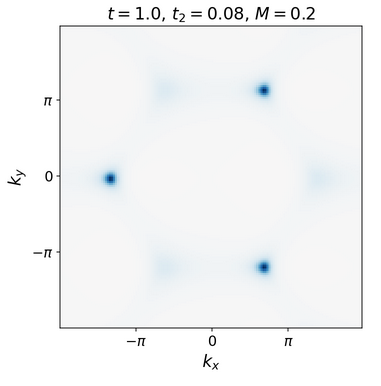
This makes it clear that the integral of the Berry curvature over the Brillouin torus – hence the first Chern number of the valence bundle – is positive in this phase. This is the statement that the Chern insulator-phase of the Haldane model at $t_2/M \gt \frac{1}{3\sqrt{3}}$ is non-trivial.

K-Theory classification?

The established K-theory classification of topological phases of matter asserts that (twisted equivariant) topological K-theory of gapped valence bundles over a full Brillouin torus classifies crystalline topological insulator-phases. For the non-symmetry protected phases relavant for the Haldane model, this is the KU-theory-classification of Chern insulators.

There has not been much systematic discussion of how to generalize this statement to a classification of topological semi-metal-phases in some flavor of topological K-theory. But the above phase behavior of of the Haldane model under deformation by constant mass terms (i.e. at $t_2 = 0$) supports the conjecture that topological semi-metal phases are classified by the (twisted, equivariant) flat differential K-theory of the complement $\widehat{T}^2 \setminus \{k_1, \cdots, k_N\}$ of the $N$ nodal points $\vec k := k_1, k_2, \cdots, k_N$ inside the Brillouin torus.

Namely, under this assumption the relevant K-theory charges form the following double complex of exact sequences:

(graphics from SS 22)

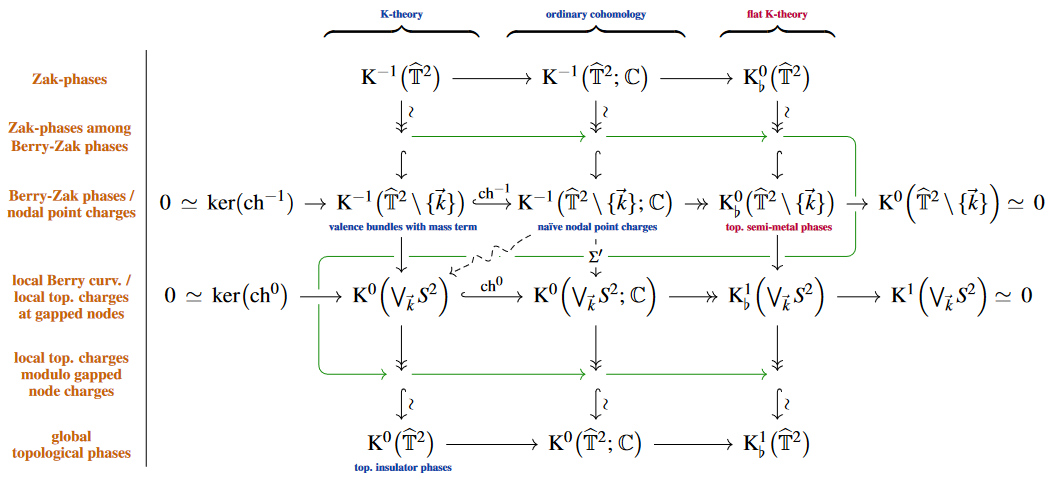
(To see that the boundary of this diagram is as shown, use the stable homotopy type of the punctured torus as shown there.)

Here the squiggly dashed arrow indicates the mathematical lifting problem which accurately encodes the above statement that topological charges associated to accidental/spurious band nodes (those which actually make for a trivial semi-metal phase, in that there exists a constant mass term that gaps out the node crossings), give rise to local Berry curvatures whose global topological charge cancels out and thus implies that also the globally gapped phase is topologically trivial:

(graphics from SS 22)

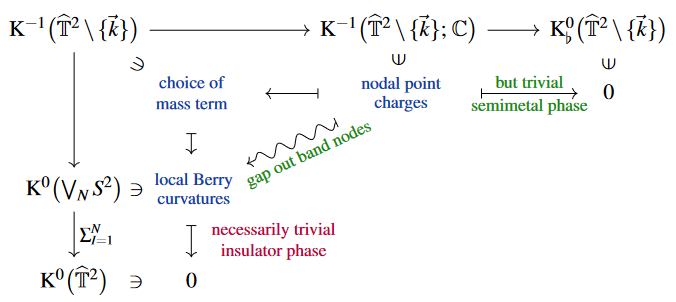
This accurately reflects what is seen above in the phase diagram of the Haldane mode, for constant mass terms $M$ (which are those that correspond to passage to $\mathrm{K}^{-1}$, by Karoubi K-theory) but in the absence of interactions ($t_2 = 0$).

Related concepts

• topological phase of matter

• K-theory classification of topological phases of matter

• Kane-Mele model

References

Theory

The original article:

• Duncan Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”, Phys. Rev. Lett. 61 (1988) 2015-2018 $[$doi:10.1103/PhysRevLett.61.2015$]$

see also

• Doru Sticlet, Frederic Piéchon, Jean-Noël Fuchs, Pavel Kalugin, Pascal Simon, Section 2.B.1 (pp. 3) of: Geometrical engineering of a two-bands Chern insulator in two dimensions with arbitrary topological index, Phys. Rev. B 85 165456 (2012) $[$arXiv:1201.6613, doi:10.1103/PhysRevB.85.165456$]$

Review:

• Online course on topology in condensed matter,Haldane model, Berry curvature, and Chern number* (2015-) $[$topocondmat.org/w4_haldane/haldane_model.html$]$

• Jonathan Atteia, Topology and electronic transport in Dirac systems under irradiation (2016) $[$tel:[phone], pdf$]$

• David Vanderbilt, Section 5.1.1 of: Berry Phases in Electronic Structure Theory – Electric Polarization, Orbital Magnetization and Topological Insulators, Cambridge University Press (2018) (doi:10.1017/9781316662205)

• Tudor D. Stanescu, Section 7.2.1 of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press 2020 (ISBN:9780367574116)

• Jérôme Cayssol, Jean-Noël Fuchs, Section IV.C of: Topological and geometrical aspects of band theory, J. Phys. Mater. 4 (2021) 034007 (arXiv:2012.11941, doi:10.1088/2515-7639/abf0b5)

Modified Haldene model for Chern insulators:

• Doru Sticlet, Frédéric Piéchon, Jean-Noël Fuchs, Pavel Kalugin, Pascal Simon, Geometrical engineering of a two-bands Chern insulator in two dimensions with arbitrary topological index, Phys. Rev. B 85 165456 (2012) [arXiv:1201.6613, doi:10.1103/PhysRevB.85.165456]

• Marwa Mannaï, Jean-Noël Fuchs, Frédéric Piéchon, Sonia Haddad, Stacking-induced Chern insulator [arXiv:2208.02491]

Much of the above material follows:

• Delft Topology Course team, Haldane model, Berry curvature, and Chern number

Some of the above material is taken from:

• Hisham Sati, Urs Schreiber: Anyonic topological order in TED K-theory

Experiment

Realization in experiment:

• Gregor Jotzu, Michael Messer, Rémi Desbuquois, Martin Lebrat, Thomas Uehlinger, Daniel Greif, Tilman Esslinger:

  Experimental realization of the topological Haldane model with ultracold fermions, Nature 515 (2014) 237–240 (doi:10.1038/nature13915)