nLab variational bicomplex
Context
Variational calculus
Differential geometric version
Derived differential geometric version
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
For a (spacetime) manifold and a bundle (in physics called the field bundle) with jet bundle , the variational bicomplex is essentially the de Rham complex of with differential forms bigraded by horizontal degree (with respect to ) and vertical degree (along the fibers of )). Accordingly the differential decomposes as
where is the de Rham differential on , is called the horizontal differential and is called the vertical differential.
With thought of as a field bundle over spacetime/worldvolume, then is a measure for how quantities change over spacetime, while is the variational differential that measures how quantities change as the field configurations are varied.
Accordingly, much of classical mechanics and classical field theory on is formalized in terms of the variational bicomplex. For instance
-
a field configuration is a section of ;
-
a Lagrangian is an element ;
-
a local action functional is a map
of the form
-
the Euler-Lagrange equation is
-
the covariant phase space is the locus
-
a conserved current is an element that is horizontally closed on the covariant phase space
-
a symmetry is an evolutionary vector field such that
-
Noether's theorem asserts that every symmetry induces a conserved current.
Definition
Let be a smooth manifold and some smooth bundle over . Write for the corresponding jet bundle.
The bicomplex
The spaces of sections and canonically inherit a generalized smooth structure that makes them diffeological spaces: we have a pullback diagram of diffeological spaces
This induces the evaluation map
and composed with the jet prolongation
it yields a smooth map (homomorphism of diffeological spaces)
Write
for the cochain complex of smooth differential forms on the product , bigraded with respect to the differentials on the two factors
where the , and , are the de Rham differentials of , and , respectively.
Definition
The variational bicomplex of is the sub–bi-complex of that is the image of the pullback of forms along the map (1):
We write
and speak of the bicomplex of local forms on sections on .
The bicomplex structure on is attributed in (Olver 86) to (Takens 79). The above formulation as a sub-bicomplex of the evident bicomplex of forms on is due to [Zuckerman 87, p. 5].
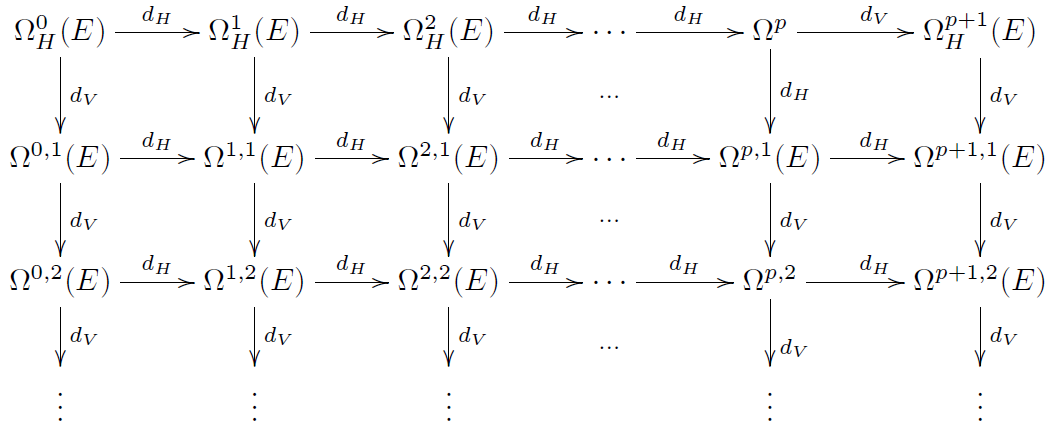
More on the horizontal differential complex
Remark
In terms of a coordinate chart of covering a coordinate chart of , the action of the horizontal differential on functions is given by the formula for the total derivative operation, but with concrete differentials substituted by the respective jet coordinates:
More abstractly, the horizontal differential is characterized as follows:
Proposition
The horizontal differential takes horizontal forms to horizontal forms, and for all sections it respects pullback of differential forms along the jet prolongation
(where on the right we have the ordinary de Rham differential on the base space).
Yet more abstractly, the horizontal complex may be understood in terms of differential operators and the jet comonad as follows.
Remark
A horizontal differential -form on is equivalently a homomorphism of bundles over
from the jet bundle to the exterior bundle . This in turn is, by the discussion there, equivalently a differential operator .
Now of course also the de Rham differential on is a differential operator . In view of this, the horizontal differential of the variational bicomplex is just the composition operation of differential operators, with horizontal forms regarded as differential operators as above.
By the fact that differential operators are the co-Kleisli morphisms of the Jet comonad, this means that the horizontal differential is
(e.g. Krasil’shchik-Verbovertsky 98, around def. 3.27, Krasil’shchik-Vinogradov 99, ch 4, around def. 1.8)
Evolutionary vector fields
Vector fields on also split into a direct sum of vertical and horizontal ones, respectively being annihilated by contraction with any horizontal -forms or with any vertical -forms, . A special kind of vertical vector field is called an evolutionary vector field provided it satisfies and , we denote the subspace of evolutionary vector fields as .
Properties
Horizontal, vertical, and total cohomology
Let be a smooth fiber bundle over a base smooth manifold of dimension Write for the jet bundle of .
Write
for the projection of -forms to the image of the “interior Euler operator” (Anderson 89, p. 21 (50/318)).
Proposition
(Takens acyclicity theorem)
The cochain cohomology of the Euler-Lagrange complex
is isomorphic to the de Rham cohomology of the total space of the given fiber bundle.
For smooth functions of locally bounded jet order this is due to (Takens 79). A proof is also in (Anderson 89, theorem 5.9).
For smooth functions of globally bounded order and going up to the Euler-Lagrange operator , this is also shown in (Deligne 99, vol 1, p.188).
The fundamental variational formula
Definition
A source form is an element in such that
depends only on the 0-jet of .
Proposition
Let .
Then there is a unique source form such that
Moreover
-
is independent of changes of by -exact terms:
-
is unique up to -exact terms.
This is [Zuckerman 87, theorem 3].
Here is the Euler-Lagrange operator .
Definition
Write
Proposition
vanishes when restricted to vertical tangent vectors based in covariant phase space (but not necessarily tangential to it).
This is [Zuckerman 87, lemma 8].
Presymplectic covariant phase space
Corollary
The form is a conserved current.
Definition
For a compact closed submanifold of dimension , one says that
is the presymplectic structure on covariant phase space relative to .
Proposition
The 2-form is indeed closed
and in fact exact:
is its presymplectic potential .
Symmetries
Let .
Definition
An evolutionary vertical vector field is a symmetry if
Proposition
The presymplectic form from def. is annihilated by the Lie derivative of the vector field on induced by a symmetry.
This appears as [Zuckerman 87, theorem 13].
Elementary formalization in differential cohesion
We discuss aspects of an elementary formalization in differential cohesion of the concept of the variational bicomplex .
under construction
Let be a context of cohesion and differential cohesion, with
-
flat modality denoted ;
-
infinitesimal shape modality denoted .
Choose
-
an object , the base space (or spacetime or worldvolume);
-
an object , the field bundle,
-
an object , the differential coefficients.
Write
-
for the base change adjoint triple over , the étale geometric morphism of the slice (infinity,1)-topos ;
-
for the external space of sections functor;
-
for the -component of the unit of ;
-
for the induced jet comonad;
-
for the Eilenberg-Moore category of -coalgebras (the objects are differential equations with variables in , the morphisms are differential operators between these, preserving solution spaces), manifested as a topos of coalgebras over ;
the (non-full) direct image of this geometric morphism is the co-Kleisli category of the jet comonad and so for a morphism in , we write for the corresponding co-Kleisli morphism in ;
We record the following simple fact, which holds generally since the jet comonad is a right adjoint (to the infinitesimal disk bundle functor), hence preserves terminal objects, and is the terminal object:
Definition
The jet prolongation map
is the the Jet functor itself, regarded, in view of prop. , as taking sections to sections via
Definition
For a bundle over , then a horizontal -form on the jet bundle is a morphism in of the form
For a morphism in , then the induced horizontal differential is the operation of horizontal forms sending to the composite
Remark
Since all objects in def. are in the co-Kleisli category of the jet comonad, the morphism there is equivalently a morphism in of the form
For the special case that in def. , then and so a horizontal -form on we call just a an -form.
Proposition
The horizontal differential of def. commutes with pullback of horizontal differential forms along the jet prolongation, def. , of any field section .
In detail: for
then there is a natural equivalence
Proof
Since all objects are in the direct image , this is an equivalence of morphisms in the co-Kleisli category of the jet comonad, hence is equivalently an equivalence of co-Kleisli composites of morphisms in .
As such, the left hand side of the equality is given in by the composite morphism
thought of as bracketed to the right. By naturality of the Jet-counit this is equivalently
By functorality of this is equivalent to
which is the right hand side of the equivalence to be proven.
Related concepts
References
The variational bicomplex was introduced independently in
-
Alexandre Vinogradov, A spectral sequence associated with a non-linear differential equation, and the algebro-geometric foundations of Lagrangian field theory with constraints , Sov. Math. Dokl. 19 (1978) 144–148.
-
W. M. Tulczyjew, The Euler-Lagrange resolution , in Lecture Notes in Mathematics 836 22–48 (Springer-Verlag, New York 1980).
-
T. Tsujishita, On variation bicomplexes associated to differential equations, Osaka J. Math. 19 (1982), 311–363.
See also
-
Floris Takens, A global version of the inverse problem of the calculus of variations J. Diff. Geom. 14 (1979) 543-562
An introduction is in
- Ian Anderson, Introduction to the variational bicomplex, in Mathematical aspects of classical field theory, Contemp. Math. 132 (1992) 51–73, gBooks
A careful discussion that compares the two versions (one over smooth functions globally of finite jet order, one over smooth functions locally of finite jet order) is in
- G. Giachetta, L. Mangiarotti, Gennadi Sardanashvily, Cohomology of the variational bicomplex on the infinite order jet space, Journal of Mathematical Physics 42, 4272-4282 (2001) (arXiv:math/0006074)
Textbook accounts include
-
Peter Olver, section 5.4 of Applications of Lie groups to differential equations, Springer Graduate Texts in Mathematics 107 (1986)
-
Ian Anderson, The variational bicomplex, Utah State University 1989 (pdf)
-
Joseph Krasil'shchik, Alexander Verbovetsky, Homological Methods in Equations of Mathematical Physics (arXiv:math/9808130)
-
Joseph Krasil'shchik, Alexandre Vinogradov et al. (eds.) Symmetries and Conservation Laws for Differential Equations of Mathematical Physics, AMS 1999
Other surveys include
- Juha Pohjanpelto, Symmetries, Conservation Laws, and Variational Principles for Differential Equations (2014) (pdf slides)
An early discussion with application to covariant phase spaces and their presymplectic structure is in
- Gregg Zuckerman, Action principles and global geometry, in: Shing-Tung Yau (ed.) Mathematical Aspects of String Theory, World Scientific (1987) 259-284 [pdf, doi:10.1142/0383]
An invariant version (under group action) is in
- Irina Kogan, Peter Olver, The invariant variational bicomplex, pdf
A more detailed version of this is in
- Irina Kogan, Peter Olver, Invariant Euler-Lagrange Equations and the Invariant Variational Bicomplex, pdf
See also
- Victor Kac, An explicit construction of the complex of variational calculus and Lie conformal algebra cohomology, talk at Algebraic Lie Theory, Newton Institute 2009, video
An application to multisymplectic geometry is discussed in
- Thomas Bridges, Peter Hydon, Jeffrey Lawson, Multisymplectic structures and the variational bicomplex (pdf)
Discussion in the context of supergeometry is in
- Gennadi Sardanashvily, Grassmann-graded Lagrangian theory of even and odd variables (arXiv:1206.2508)
Discussion in the convenient context of smooth sets:
- Grigorios Giotopoulos, Hisham Sati, §5.1 & §7.1 in: Field Theory via Higher Geometry I: Smooth Sets of Fields [arXiv:2312.16301]
Last revised on December 29, 2023 at 13:17:05. See the history of this page for a list of all contributions to it.