nLab G₂

Idea

The Lie group $G_2$ is one (or rather: three) of the exceptional Lie groups. One way to characterize it is as the automorphism group of the octonions as a normed algebra:

$$G_2 = Aut(\mathbb{O}) \,.$$

Another way to characterize it is as the stabilizer subgroup inside the general linear group $GL(7)$ of the canonical differential 3-form $\langle ,(-)\times (-) \rangle$ on the Cartesian space $\mathbb{R}^7$

$$G_2 \simeq Stab_{GL(7)}(\langle -, -\times -\rangle) \,.$$

As such, the group $G_2$ is a higher analog of the symplectic group (which is the group that preserves a canonical 2-form on any $\mathbb{R}^{2n}$), obtained by passing from symplectic geometry to 2-plectic geometry.

Definition

Definition

On the Cartesian space $\mathbb{R}^7$ consider the associative 3-form, the constant differential 3-form $\omega \in \Omega^3(\mathbb{R}^7)$ given on tangent vectors $u,v,w \in \mathbb{R}^7$ by

$$\omega(u,v,w) \coloneqq \langle u , v \times w\rangle \,,$$

where

• $\langle -,-\rangle$ is the canonical bilinear form

• $(-)\times(-)$ is the cross product of vectors.

Then the group $G_2 \hookrightarrow GL(7)$ is the subgroup of the general linear group acting on $\mathbb{R}^7$ which preserves the canonical orientation and preserves this 3-form $\omega$. Equivalently, it is the subgroup preserving the orientation and the Hodge dual differential 4-form $\star \omega$.

See for instance the introduction of Joyce 1996.

Properties

Orientation

The inclusion $G_2 \hookrightarrow GL(7)$ of def. factors through the special orthogonal group

$$G_2 \hookrightarrow SO(7) \hookrightarrow GL(7) \,.$$

Dimension

The dimension of (the manifold underlying) $G_2$ is

$$dim(G_2) = 14 \,.$$

One way to see this is via octonionic basic triples $(e_1, e_2, e_3) \in \mathbb{O}^3$ and the fact (this proposition) that these form a torsor over $G_2$, hence that the space of them has the same dimension as $G_2$:

• the space of choices for $e_1$ is the 6-sphere of imaginary unit octonions;

• given that, the space of choices for $e_2$ is a 5-sphere of imaginary unit octonions orthogonal to $e_1$;

• given that, then the space of choices for $e_3$ is the 3-sphere of imaginary unit octonions orthogonal to both $e_1$ and $e_2$.

Hence

$$dim(G_2) = dim(S^6) + dim(S^5) + dim(S^3) = 14 \,.$$

(e.g. Baez, 4.1)

Cohomology

The Dwyer-Wilkerson space $G_3$ (Dwyer-Wilkerson 93) is a 2-complete H-space, in fact a finite loop space/infinity-group, such that the mod 2 cohomology ring of its classifying space/delooping is the mod 2 Dickson invariants of rank 4. As such, it is the fourth and last space in a series of infinity-groups that starts with 3 compact Lie groups:

$n=$	1	2	3	4
$DI(n)=$	Z/2	SO(3)	G2	G3
	= Aut(C)	= Aut(H)	= Aut(O)

Subgroups

We discuss various subgroups of $G_2$.

Definition

Write

• $G_2 = Aut(\mathbb{O})$, the automorphism group of the octonions as a normed alegbra,

• $Stab_{G_2}(\mathbb{H})$, the stabilizer subgroup of the quaternions inside the octonions, i.e. of elements $\sigma\in G_2$ such that $\sigma_{|\mathbb{H}}\colon \mathbb{H}\to \mathbb{H} \hookrightarrow\mathbb{O}$;

• $Fix_{G_2}(\mathbb{H})$ for the further subgroup of elements that fix each quaternions (the “elementwise stabilizer group”), i.e. those $\sigma$ with $\sigma_{\vert \mathbb{H}} = id_{\mathbb{H}}$.

Proposition

The elementwise stabilizer group of the quaternions is SU(2):

$$Fix_{G_2}(\mathbb{H}) \simeq SU(2) \,.$$

Proof

Consider octonionic basic triples $(e_1, e_2, e_3) \in \mathbb{O}^3$ and the fact (this proposition) that these form a torsor over $G_2$. The choice of $(e_1,e_2)$ is equivalently a choice of inclusion $\mathbb{H} \hookrightarrow \mathbb{O}$. Then the remaining space of choices for $e_3$ is the 3-sphere (the space of unit imaginary octonions orthogonal to both $e_1$ and $e_2$). This carries a unit group structure, and by the torsor property this is the required subgroup of $SU(2)$.

Proposition

The subgroups in def. sit in a short exact sequence of the form

$$\array{ 1 &=& 1 \\ \downarrow && \downarrow \\ Fix_{G_2}(\mathbb{H}) & \simeq & SU(2) \\ \downarrow && \downarrow \\ Stab_{G_2}(\mathbb{H}) & \simeq & SO(4) \\ \downarrow && \downarrow \\ Aut(\mathbb{H}) &\simeq& SO(3) \\ \downarrow && \downarrow \\ 1 &=& 1 }$$

exhibiting SO(4) as a group extension of the special orthogonal group $SO(3)$ by the special unitary group $SU(2)$.

(e.g. Ferolito, section 4, see also at SO(3) – Irreps)

Furthermore there is a subgroup $SU(3) \hookrightarrow G_2$ whose intersection with $SO(4)$ is $U(2)$. The simple part $SU(2)$ of this intersection is a normal subgroup of $SO(4)$.

(see e.g. Miyaoka 93)

The coset space G2/SU(3) is the 6-sphere. See there for more.

(from Kramer 02)

The Weyl group of $G_2$ is the dihedral group of order 12. (see e.g. Ishiguro, p. 3).

$\,$

Supgroups

Proposition

(coset space of Spin(7) by G₂ is 7-sphere)

Consider the canonical action of Spin(7) on the unit sphere in $\mathbb{R}^8$ (the 7-sphere),

1. This action is is transitive;

2. the stabilizer group of any point on $S^7$ is G₂;

3. all G₂-subgroups of Spin(7) arise this way, and are all conjugate to each other.

Hence the coset space of Spin(7) by G₂ is the 7-sphere

$$Spin(7)/G_2 \;\simeq\; S^7 \,.$$

(e.g Varadarajan 01, Theorem 3)

Coset quotients

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

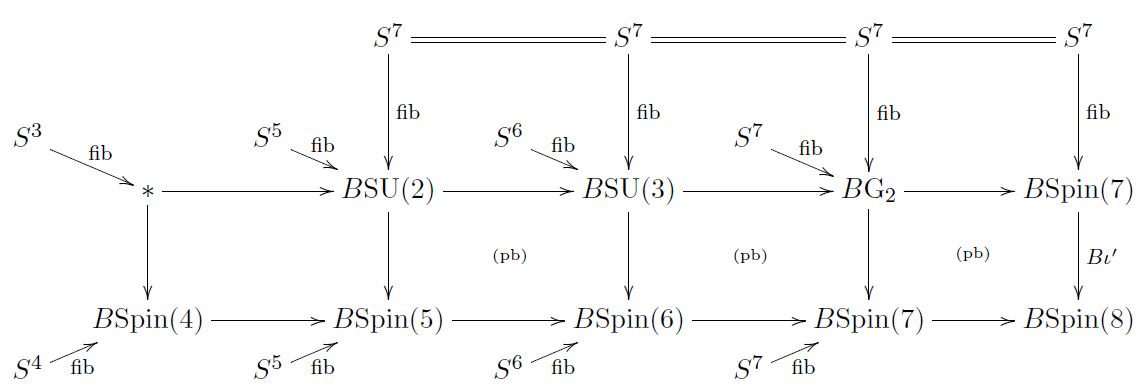
(from FSS 19, 3.4)

$G$-Structure and exceptional geometry

Spin(8)-subgroups and reductions to exceptional geometry

reduction	from spin group	to maximal subgroup
Spin(7)-structure	Spin(8)	Spin(7)
G₂-structure	Spin(7)	G₂
CY3-structure	Spin(6)	SU(3)
SU(2)-structure	Spin(5)	SU(2)
generalized reduction	from Narain group	to direct product group
generalized Spin(7)-structure	$Spin(8,8)$	$Spin(7) \times Spin(7)$
generalized G₂-structure	$Spin(7,7)$	$G_2 \times G_2$
generalized CY3	$Spin(6,6)$	$SU(3) \times SU(3)$

see also: coset space structure on n-spheres

Relation to higher prequantum geometry

The 3-form $\omega$ from def. we may regard as equipping $\mathbb{R}^7$ with 2-plectic structure. From this point of view $G_2$ is the linear subgroup of the 2-plectomorphism group, hence (up to the translations) the image of the Heisenberg group of $(\mathbb{R}^7, \omega)$ in the symplectomorphism group.

Or, dually, we may regard the 4-form $\star \omega$ of def. as being a 3-plectic structure and $G_2$ correspondingly as the linear part in the 3-plectomorphism group of $\mathbb{R}^7$.

As zero-divisors of the sedenions

It is shown in Corollary 2.14 of Moreno (1997) that the group of zero-divisors of the sedenions is isomorphic to $G_2$.

Related concepts

• G₂ manifold, generalized G₂-manifold

• M-theory on G₂-manifolds, G₂-MSSM

• G₂, F₄,

  E₆, E₇, E₈, E₉, E₁₀, E₁₁, $\cdots$

classification of special holonomy manifolds by Berger's theorem:

	$\,$G-structure$\,$	$\,$special holonomy$\,$	$\,$dimension$\,$	$\,$preserved differential form$\,$
$\,\mathbb{C}\,$	$\,$Kähler manifold$\,$	$\,$U(n)$\,$	$\,2n\,$	$\,$Kähler forms $\omega_2\,$
	$\,$Calabi-Yau manifold$\,$	$\,$SU(n)$\,$	$\,2n\,$
$\,\mathbb{H}\,$	$\,$quaternionic Kähler manifold$\,$	$\,$Sp(n).Sp(1)$\,$	$\,4n\,$	$\,\omega_4 = \omega_1\wedge \omega_1+ \omega_2\wedge \omega_2 + \omega_3\wedge \omega_3\,$
	$\,$hyper-Kähler manifold$\,$	$\,$Sp(n)$\,$	$\,4n\,$	$\,\omega = a \omega^{(1)}_2+ b \omega^{(2)}_2 + c \omega^{(3)}_2\,$ ($a^2 + b^2 + c^2 = 1$)
$\,\mathbb{O}\,$	$\,$Spin(7) manifold$\,$	$\,$Spin(7)$\,$	$\,$8$\,$	$\,$Cayley form$\,$
	$\,$G₂ manifold$\,$	$\,$G₂$\,$	$\,7\,$	$\,$associative 3-form$\,$

References

General

• Tonny Springer, Ferdinand Veldkamp, chapter 2 of Octonions, Jordan Algebras, and Exceptional Groups, Springer Monographs in Mathematics, 2000

Surveys are in

• Spiro Karigiannis, What is… a $G_2$-manifold (pdf)

• Simon Salamon, A tour of exceptional geometry, (pdf)

• Wikipedia, G₂ .

The definitions are reviewed for instance in

• Dominic Joyce, Compact Riemannian 7-manifolds with holonomy $G_2$, Journal of Differential Geometry 43 2 (1996) [doi:10.4310/jdg/1214458109, pdf]

• Ferolito The octonions and $G_2$ (pdf)

• John Baez, section 4.1 G2 of: The Octonions (arXiv:math/0105155)

• Ruben Arenas, Constructing a Matrix Representation of the Lie Group $G_2$, 2005 (pdf)

Discussion in terms of the Heisenberg group in 2-plectic geometry is in

• Alberto Ibort, Multisymplectic geometry: generic and exceptional, Proceedings of the IX Fall workshop on geometry and physics (pdf)

A description of the root space decomposition of the Lie algebra $\mathfrak{g}_2$ is in

• Tathagata Basak, Root space decomposition of $\mathfrak{g}_2$ from octonions, arXiv:1708.02367

As the group of zero divisors of the sedenions

• Guillermo Moreno. The zero divisors of the Cayley-Dickson algebras over the real numbers. (1997) (doi)

Cohomological properties are discussed in

• Younggi Choi, Homology of the gauge group of exceptional Lie group $G_2$, J. Korean Math. Soc. 45 (2008), No. 3, pp. 699–709

Discussion of subgroups includes

• Reiko Miyaoka, The linear isotropy group of $G_2/SO(4)$, the Hopf fibering and isoparametric hypersurfaces, Osaka J. Math. Volume 30, Number 2 (1993), 179-202. (Euclid)

• Kenshi Ishiguro, Classifying spaces and a subgroup of the exceptional Lie group $G_2$ pdf

• Linus Kramer, 4.27 of Homogeneous Spaces, Tits Buildings, and Isoparametric Hypersurfaces, AMS 2002

Discussion of $G_2$ as a subgroup of Spin(7):

• Veeravalli Varadarajan, Spin(7)-subgroups of SO(8) and Spin(8), Expositiones Mathematicae, 19 (2001): 163-177 (pdf)

Applications in physics

Discussion of Yang-Mills theory with $G_2$ as gauge group is in

• Ernst-Michael Ilgenfritz, Axel Maas, Topological aspects of $G_2$ Yang-Mills theory (arXiv:1210.5963)