nLab exceptional geometry

Idea

The classification of Riemannian manifolds with special holonomy contains two “exceptional” cases: G2-holonomy in dimension 7, and Spin(7)-holonomy in dimension 8. Their study is the topic of exceptional geometry.

Sometimes more generally, exceptional geometry is understood to study spaces controled by exceptional Lie groups in some way.

Properties

In terms of twisted Cohomotopy

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G2 is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G2/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

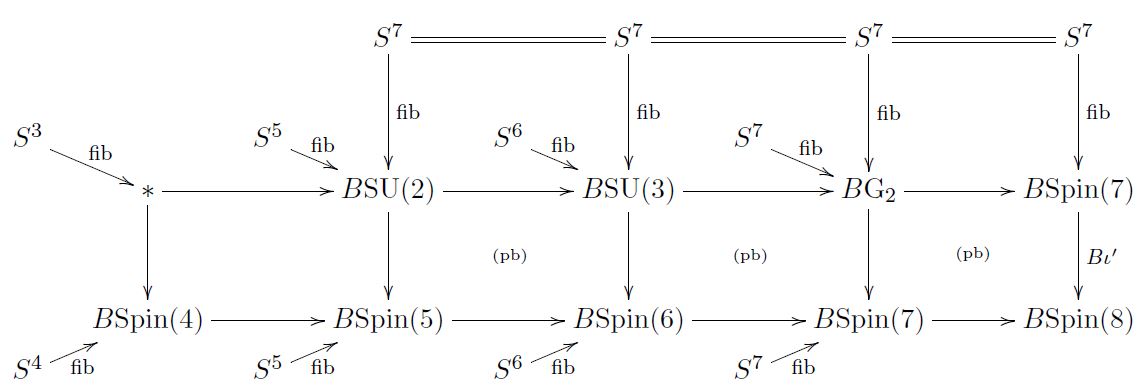
(from FSS 19, 3.4)

Related concepts

• exceptional Lie group

• exceptional generalized geometry

• exceptional field theory

• universal exceptionalism

References

General

General discussion is in

• Dominic Joyce, The exceptional holonomy groups and calibrated geometry (pdf)

• Simon Salamon, A tour of exceptional geometry (pdf)

• Simon Salamon, Self-duality and exceptional geometry (pdf)

Discussion of G2 manifolds is in

• Spiro Karigiannis, $G_2$-manifolds – Exceptional structures in geometry arising from exceptional algebra (pdf)

In supergravity

Applications to KK-compactification of 11d supergravity (see also at M-theory on G2-manifolds) is discussed in

• George Papadopoulos, Paul Townsend, Compactifications of $D = 11$ supergravity on spaces of exceptional holonomy (arXiv:hep-th/9506150)

• K. Koepsell, Hermann Nicolai, Henning Samtleben, An exceptional geometry for d=11 supergravity? (arXiv:hep-th/0006034)

• Chris Hull, Generalised Geometry for M-Theory, JHEP 0707:079, 2007 (arXiv:hep-th/0701203)

For more along these lines see the references at exceptional generalized geometry.

As M-brane target space

Discusssion of M-brane sigma-models on exceptional geometry target spaces:

• Yuho Sakatani, Shozo Uehara, Branes in Extended Spacetime: Brane Worldvolume Theory Based on Duality Symmetry, Phys. Rev. Lett. 117 191601 (2016) [arXiv:1607.04265, talk slides]

• Yuho Sakatani, Shozo Uehara, Exceptional M-brane sigma models and $\eta$-symbols [arXiv:1712.10316]