nLab Sullivan chord diagram

Idea

A Sullivan chord diagram (Cohen-Godin 03, Def. 1, following Chas-Sullivan 02) is a finite undirected graph given by attaching the external vertices of trees, equipped with cyclic ordering around their vertices, to a number of embedded oriented circles, e.g.

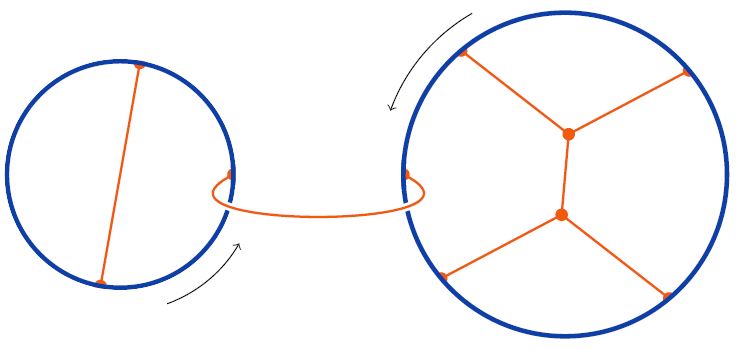
such that the embedded circles are boundary components of the induced ribbon graph surface:

graphics from Sati-Schreiber 19c

This way Sullivan chord diagrams $D$ induce 2-dimensional cobordisms, namely cospans of topological spaces,

$$\array{ && \Sigma_D \\ & \nearrow && \nwarrow \\ \mathllap{ \big( \underset{q}{\sqcup} S^1 \big) \simeq \; } \partial_{in}\Sigma_D && && \partial_{out} \Sigma_D \mathrlap{ \; \simeq \big( \underset{p}{\sqcup} S^1 \big) } }$$

with the induced ribbon graph surface $\Sigma_D$ at the tip, the $p$ boundary components corresponding to the embedded circles (shown above in grey) as one leg, and the remaining $q$ boundary components (shown in blue) as the other.

Applying to this cospan the space of maps-functor $Maps(-,X)$ into any topological space $X$, yields a span/correspondence

$$\array{ && Maps(\Sigma_D, X) \\ & \swarrow && \searrow \\ \big(\mathcal{L}X\big)^q && && \big(\mathcal{L}X\big)^p }$$

between products of the free loop space of $X$ with itself. The induced integral transform operations on the ordinary homology of the free loop spaces are generalized string topology-operation (Cohen-Godin 03, Section 2).

(It is for this integral transform construction that the complement of the embedded circles is required to be a tree, for this allows to contract the spaces of maps out of these components, up to homotopy.)

Sullivan chord diagrams also naturally act on Hochschild homology/cyclic homology (Tradler-Zeinalian 04, Tradler-Zeinalian 06).

Properties

Relation to round chord diagrams

Every round chord diagram is also a Sullivan chord diagram.

Relation to Jacobi diagrams

Sullivan chord diagrams are much like Jacobi diagrams, but more general in that they may have more than one (disjointly) embedded circle and in that they are not required to be trivalent, and less general in that the complement of the embedded circles is required to be a disjoint union of trees. The last condition need not be satisfied by Jacobi diagrams, and hence not every Jacobi diagram is a Sullivan diagram.

For example, the following Jacobi diagram is NOT a Sullivan chord diagram:

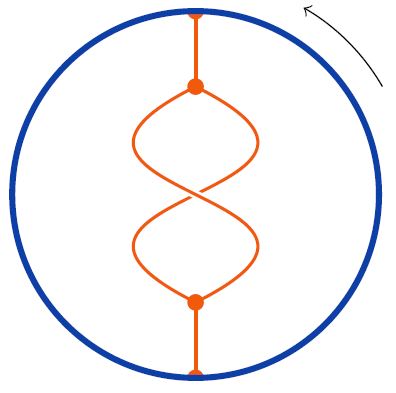
Relation to horizontal chord diagrams

One obtains Sullivan chord diagrams with $p$ disjoint embedded circles from horizontal chord diagrams by closing up strands after acting with a permutation with $p$ cycles ($p$ orbits)

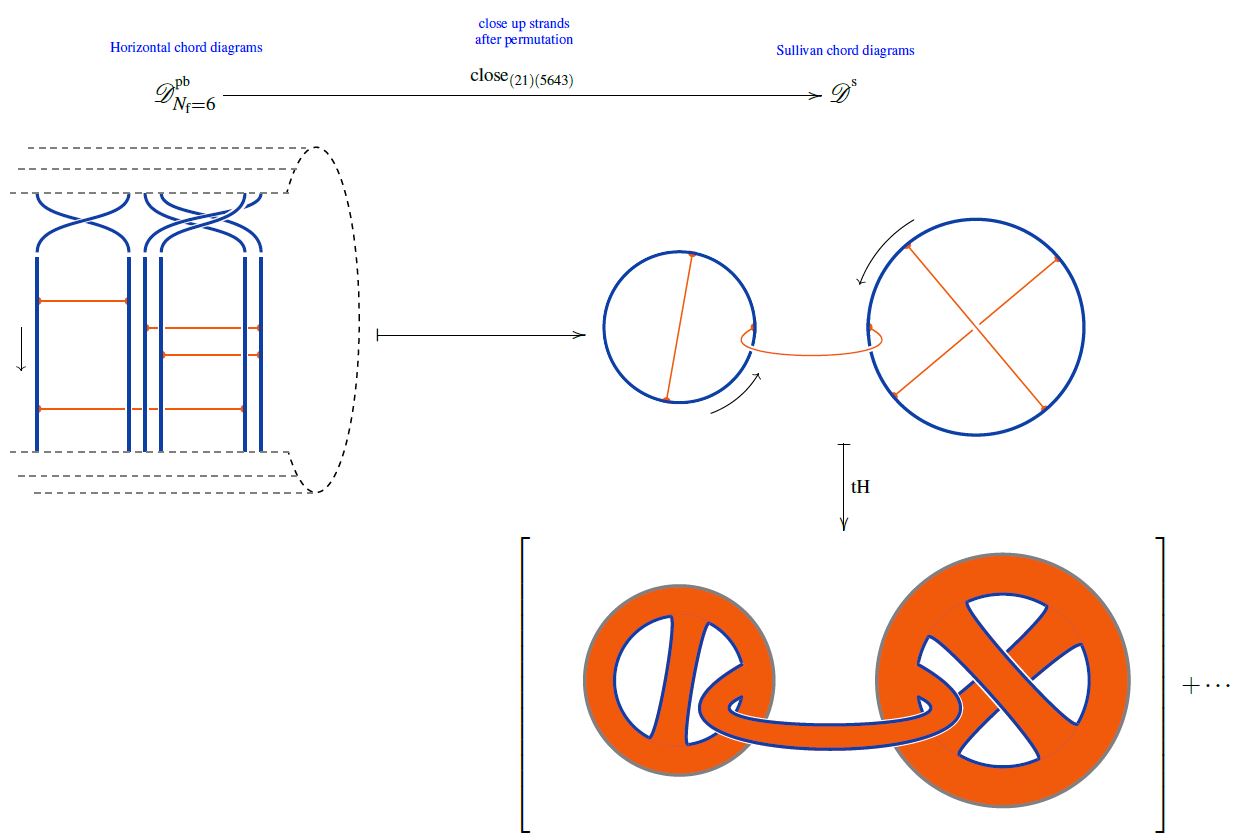
graphics from Sati-Schreiber 19c

Related concepts

chord diagrams	weight systems
linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams	Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems

knots	braids
chord diagram, Jacobi diagram	horizontal chord diagram
1T&4T relation	2T&4T relation/ infinitesimal braid relations
weight system	horizontal weight system
Vassiliev knot invariant	Vassiliev braid invariant
weight systems are associated graded of Vassiliev invariants	horizontal weight systems are cohomology of loop space of configuration space

Applications

Chord diagrams as multi-trace observables in the BMN matrix model

The supersymmetric states of the BMN matrix model are temporally constant complex matrices which are complex metric Lie representations $\mathfrak{g} \otimes V \overset{\rho}{\to} V$ of $\mathfrak{g}=$su(2) (interpreted as fuzzy 2-sphere noncommutative geometries of giant gravitons or equivalently as fuzzy funnels of D0-D2 brane bound states).

A fuzzy 2-sphere-rotation invariant multi-trace observable on these supersymmetric states is hence an expression of the following form:

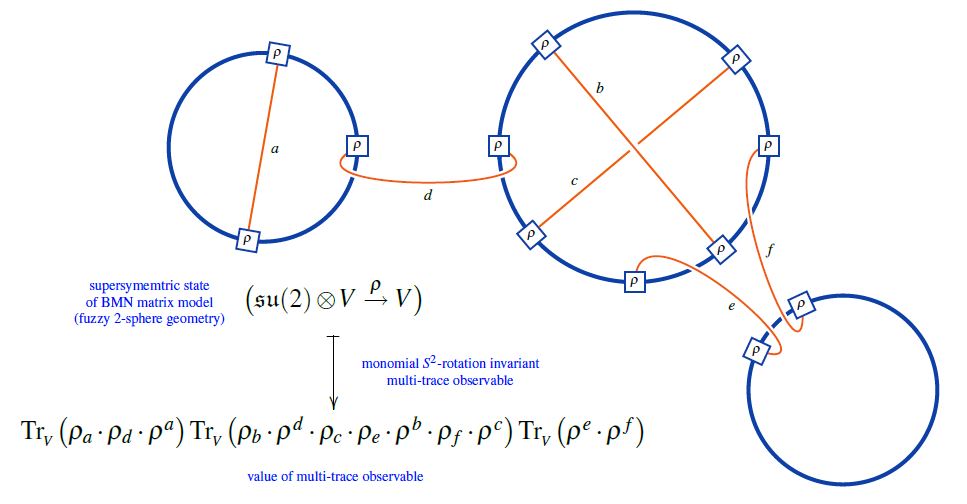
(from Sati-Schreiber 19c)

Here we are showing the corresponding string diagram/Penrose notation for metric Lie representations, which makes manifest that

1. these multi-trace observables are encoded by Sullivan chord diagrams $D$

2. their value on the supersymmetric states $\mathfrak{su}(2) \otimes V \overset{\rho}{\to}V$ is the evaluation of the corresponding Lie algebra weight system $w_{{}_V}$ on $D$.

Or equivalently, if $\widehat D$ is a horizontal chord diagram whose $\sigma$-permuted closure is $D$ (see here) then the values of the invariant multi-trace observables on the supersymmetric states of the BMN matrix model are the evaluation of $w_{V,\sigma}$ on $\widehat D$, as shown here:

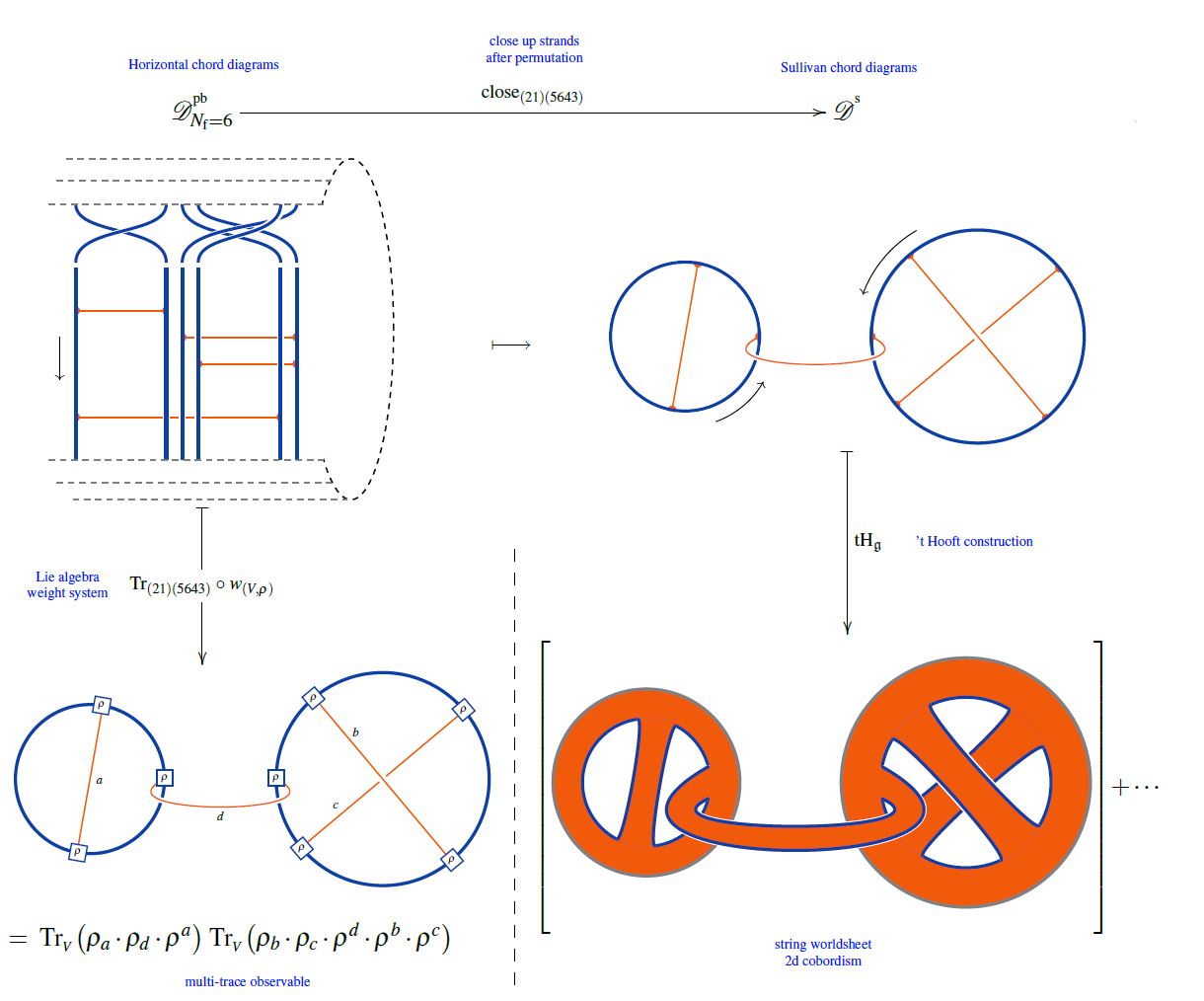
(from Sati-Schreiber 19c)

But since all horizontal weight systems are partitioned Lie algebra weight systems this way, this identifies supersymmetric states of the BMN matrix model as seen by invariant multi-trace observables as horizontal chord diagrams evaluated in Lie algebra weight systems.

References

In string topology:

The definition is due to

• Ralph Cohen, Veronique Godin, A Polarized View of String Topology, In: Graeme Segal, Ulrike Tillmann (eds.) Topology, Geometry and Quantum Field Theory, LMS, Lecture Notes Series 308, 2004 (arXiv:math/0303003, doi:10.1017/CBO9780511526398.008)

following

• Moira Chas, Dennis Sullivan, Closed string operators in topology leading to Lie bialgebras and higher string algebra, In: O.A. Laudal , R. Piene (eds.) The Legacy of Niels Henrik Abel, Springer 2004 (arXiv:math/0212358, doi:10.1007/978-3-642-18908-1_27)

Also:

• Ralph Kaufmann, Def. 1.4 of: Moduli space actions on the Hochschild Co-Chains of a Frobenius algebra I: Cell Operads (arXiv:math/0606064)

Review:

• Ralph Cohen, Alexander Voronov, around Def. 3.2.2 in: Notes on string topology (arXiv:math/0503625)

• Ralph Kaufmann, Section 4.6 of: Graphs, Strings, and Actions, In: Tschinkel Y., Zarhin Y. (eds.) Algebra, Arithmetic, and Geometry, Progress in Mathematics, vol 270. Birkhäuser 2009 (doi:10.1007/978-0-8176-4747-6_5)

Action on Hochschild homology:

• Thomas Tradler, Mahmoud Zeinalian, On the Cyclic Deligne Conjecture, Journal of Pure and Applied Algebra, Volume 204, Issue 2, 1 February 2006, Pages 280-299 (arXiv:math/0404218, doi:10.1016/j.jpaa.2005.04.009)

• Thomas Tradler, Mahmoud Zeinalian, Algebraic String Operations, K-Theory v. 38, n. 1 (November, 2007): 59-82 (arXiv:math/0605770, doi:10.1007/s10977-007-9005-2)