nLab orbit category

Idea

The orbit category of a group $G$ is the category of “all kinds” of orbits of $G$, namely of all suitable coset spaces regarded as G-spaces.

Definition

Definition

Given a topological group $G$ the orbit category $\operatorname{Orb}_G$ (denoted also $\mathcal{O}_G$) is the category whose

• objects are the homogeneous spaces (coset spaces, $G$-orbit types) $G/H$, where $H$ is a closed subgroup of $G$,

• morphisms are the $G$-equivariant continuous functions.

(e.g. tom Dieck 1987, I (10.1))

Remark

Warning: This should not be confused with the situation where a group $G$ acts on a groupoid $\Gamma$ so that one obtains the orbit groupoid.

Remark

For suitable continuous actions of $G$ on a topological space $X$, every orbit of the action is isomorphic to one of the coset spaces $G/H$ (the stabilizer group of any point in the orbit is conjugate to $H$). This is the sense in which def. gives “the category of all $G$-orbits”.

Remark

Def. yields a small topologically enriched category (though of course if $G$ is a discrete group, the enrichment of $\operatorname{Orb}_G$ is likewise discrete).

Of course, like any category, it has a skeleton, but as usually defined it is not itself skeletal, since there can exist distinct subgroups $H$ and $K$ such that $G/H \cong G/K$.

Remark

($G$-sets are the free coproduct completion of $G$-orbits)
Let $G \,\in\, Grp(Set)$ be a discrete group. Since every G-set $X$ decomposes as a disjoint union of transitive actions, namely of orbits of elements of $X$, the defining inclusion of the orbit category into $G Set$ exhibits the latter as its free coproduct completion (see also this Prop.).

Remark

(families of subgroups)
More generally, given a family $\mathcal{F}$ of subgroups of $G$ which is closed under conjugation and taking subgroups one looks at the full subcategory $\mathrm{Orb}_F\,G \subset \operatorname{Orb}_G$ whose objects are those $G/H$ for which $H\in F$. For such families, many of the considerations of results such as Elmendorf's theorem will still hold.

Equivariant Postnikov tower

Given a topological G-space, there is (following tom Dieck 1987, Sec. I.10) a sequence of variants (enhancements) of the $G$-orbit category which mixes transitions between the fixed loci with n-truncations of their homotopy types.

Equivariant set of connected components

(…)

tom Dieck 1987, Sec. I.10

(…)

Equivariant fundamental groupoid

Definition

For $G \,\in\, Grp(Set)$ a discrete group and $G \curvearrowright X \,\in\, G Act(TopSp)$ a topological $G$-space, its fundamental category (tom Dieck 1987 (10.7), Lück 1989, 8.15) or equivariant fundamental groupoid (Pronk & Scull 2021, Def. 3.1)

is the small category whose

• objects are pairs consisting of a subgroup $H \subset G$ and a $G$-equivariant function $\; x_X \,\colon\, G/H \to X$, hence, equivalently, a point in the fixed locus $X^H$;

• morphisms$x_H \xrightarrow{ (\phi,[\gamma]) } x'_{H'}$ are pairs consisting of a $G$-equivariant function $G/H \xrightarrow{ \phi } G/H'$ and a relative $G$-homotopy class $[\gamma]$ of a continuous path $\gamma \,\colon\, G/H \times [0,1] \xrightarrow{\;} X$ from $\gamma(0) = x_H$ to $\gamma_1 = \phi^\ast x'_X'$.

Example

For $G \curvearrowright X \,=\, G \curvearrowright \ast$ the point, its fundamental category (equivariant fundamental groupoid) according to Def. is the plain orbit category $G Orbts$ (Def. ).

Proposition

(equivariant fundamental groupoid under Grothendieck construction)
If we write

$$\tau_1 \esh \big( X^{(-)}\big) \;\in\; Sh\big( G Orbt, Grpd_1 \big)$$

for the fundamental groupoid of $X$ in its incarnation as a presheaf of fixed loci over the orbit category, hence for the (2,1)-functor

(1)$$\array{ G Orbt^{op} &\xrightarrow{ \tau_1 \esh \big( X^{(-)}\big) }& Grpd_1 \\ G/H &\mapsto& \tau_1 \esh (X^H) \mathrlap{\,,} }$$

which sends $G/H$ to the ordinary fundamental groupoid of the fixed locus $X^H$, then the equivariant fundamental groupoid of $G \curvearrowright X$ (Def. ) is equivalently the Grothendieck construction

(2)$$\underset {G/H \in G Orbt} {\int} \, \tau_1 \, \esh (X^{H}) \;\;\; \in \; Grpd_1$$

on (1).

This follows by direct unwinding of the definitions; see also Pronk & Scull 2021, below Def. 3.1.

Equivariant universal cover

Definition

(equivariant universal covering)
For $G \in Grp(Set)$ a discrete group and $G \curvearrowright X \,\in\, G Act(TopSp)$ a well-behaved topological $G$-space, its equivariant universal cover (tom Dieck 1987 (10.13)) “is” the functor from the fundamental equivariant groupoid (2) of $G \curvearrowright X$ to TopSp

$$\array{ \underset {G/H \in G Orbt} {\int} \, \tau_1 \, \esh (X^{H}) &\xrightarrow{\;}& TopSp &\xrightarrow{\esh}& Grpd_{\infty} \\ x_H &\mapsto& \widehat{X^H_x} }$$

which sends $x_H \,\in\, X^H$ to the universal covering $\widehat{X_x}$ of the connected component of $x_H \,\in\, X$ given by relative-homotopy-equivalences classes of paths based at $x_H$.

Write

(3)$$G Grpd_\infty \;\coloneqq\; Sh\big( G Orbt, \, Grpd_\infty \big)$$

for the $\infty$-category of $\infty$-presheaves on the $G$-orbit category, hence for the proper $G$-equivariant homotopy theory.

For $G \curvearrowright X \,\in\, G Act(TopSp)$ a topological $G$-space, its equivariant homotopy type is

$$\esh \big(X^{(-)}\big) \;\; \in \; G Grpd_\infty \,.$$

Proposition

For $G \curvearrowright X \,\in\, G Act(TopSp)$ a topological $G$-space, its equivariant universal covering according to Def. is, under Prop. and the (infinity,1)-Grothendieck construction equivalent to the 1-truncation unit

$$\array{ \esh \big( X^{(-)}\big) \\ \big\downarrow {}^{\mathrlap{ \eta^{\tau_1} }} \\ \tau_1 \, \esh \big( X^{(-)}\big) } \;\;\; \in \; \big( G Grpd_\infty\big)_{/ \tau_1 \, \esh \big( X^{(-)}\big)} \,,$$

in that

$$\array{ \underset{G/H \in G Orbt}{\int} \esh \big( X^{H}\big) &\xrightarrow{\;}& \widehat{Grpd}_\infty \\ \big\downarrow &\swArrow& \big\downarrow \\ \underset{G/H \in G Orbt}{\int} \tau_1 \, \esh \big( X^{H}\big) & \xrightarrow{ \widehat{ X^{(-)}_{(-)} } } & Grpd_\infty \,. }$$

bottom right corner not quite right, will fix…

Examples

Example

(orbit category of Z/2Z)

For equivariance group the cyclic group of order 2:

$$G \;\coloneqq\; \mathbb{Z}_2 \;\coloneqq\; \mathbb{Z}/2\mathbb{Z} \,.$$

the orbit category looks like this:

(4)$$\mathbb{Z}_2 Orbits \;=\; \left\{ \array{ \mathbb{Z}_2/1 & \overset{ \phantom{AAAAA} }{ \longrightarrow } & \mathbb{Z}_2/\mathbb{Z}_2 \\ Aut = \mathbb{Z}_2 && Aut = 1 } \right\}$$

i.e.:

$$\begin{aligned} \mathbb{Z}_2 Orbits \big( \mathbb{Z}_2/\mathbb{Z}_2 \,,\, \mathbb{Z}_2/\mathbb{Z}_2 \big) \;\simeq\; 1 \\ \mathbb{Z}_2 Orbits \big( \mathbb{Z}_2/1 \,,\, \mathbb{Z}_2/\mathbb{Z}_2 \big) \;\simeq\; \ast \\ \mathbb{Z}_2 Orbits \big( \mathbb{Z}_2/\mathbb{Z}_2 \,,\, \mathbb{Z}_2/1 \big) \;\simeq\; \varnothing \\ \mathbb{Z}_2 Orbits \big( \mathbb{Z}_2/1 \,,\, \mathbb{Z}_2/1 \big) \;\simeq\; \mathbb{Z}_2 \end{aligned}$$

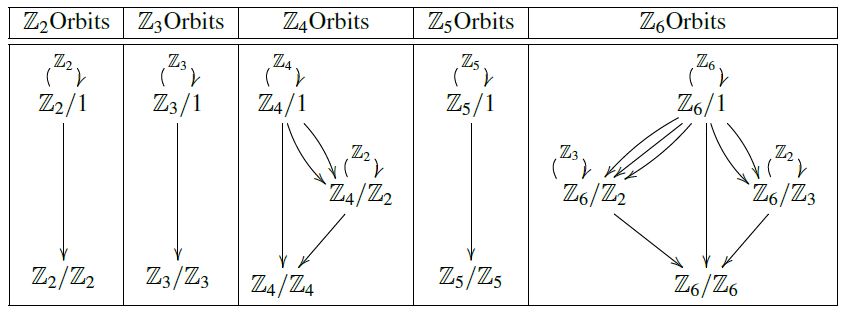
Properties

General properties

• Orbit categories as well as fundamental categories of $G$-spaces are EI-categories.

Relation to $G$-spaces and Elmendorf’s theorem

Elmendorf's theorem (see there for details) states that the (∞,1)-category of (∞,1)-presheaves on the orbit category $Orb_G$ are equivalent to the localization of topological spaces with $G$-action at the weak homotopy equivalences on fixed point spaces.

$$L_{we} G Top \simeq PSh_\infty(Orb_G) \,.$$

Relation to global equivariant homotopy theory

The $G$-orbit category is the slice (∞,1)-category of the global orbit category $Orb$ (the version with faithful functors as morphisms) over the delooping $\mathbf{B}G$:

$$Orb_G \simeq Orb_{/\mathbf{B}G} \,.$$

This means that in the general context of global equivariant homotopy theory, the orbit category appears as follows.

For more on this see also at cohesion of global- over G-equivariant homotopy theory the section the adjunction of sites.

Rezk-global equivariant homotopy theory:

cohesive (∞,1)-topos	its (∞,1)-site	base (∞,1)-topos	its (∞,1)-site
global equivariant homotopy theory $PSh_\infty(Glo)$	global equivariant indexing category $Glo$	∞Grpd $\simeq PSh_\infty(\ast)$	point
… sliced over terminal orbispace: $PSh_\infty(Glo)_{/\mathcal{N}}$	$Glo_{/\mathcal{N}}$	orbispaces $PSh_\infty(Orb)$	global orbit category
… sliced over $\mathbf{B}G$: $PSh_\infty(Glo)_{/\mathbf{B}G}$	$Glo_{/\mathbf{B}G}$	$G$-equivariant homotopy theory of G-spaces $L_{we} G Top \simeq PSh_\infty(Orb_G)$	$G$-orbit category $Orb_{/\mathbf{B}G} = Orb_G$

Relation to Mackey functors

Orbit categories are used often in the treatment of Mackey functors from the theory of locally compact groups and in the definition of Bredon cohomology.

Relation to Bredon equivariant cohomology

It appears in equivariant stable homotopy theory, where the $H$-fixed homotopy groups of a space form a presheaf on the homotopy category of the orbit category (e.g. page 8, 9 here).

Base change of equivariance groups

Example

(left base change along covering of equivariance group)
Let $\widehat{G} \overset{p}{\twoheadrightarrow} G$ be a surjective homomorphism of discrete groups. For $H \subset G$ a subgroup, write $\widehat{H} \subset \widehat{G}$ for its pullback

Then there is a reflective subcategory-inclusion of orbit categories

where

• $R(G/H) \,=\, \widehat{G}/\widehat{H}$

• $L(\widehat{G}/K) \,=\, G/p(K)$.

A transparent way to see this is to identify (as above) $G$-orbits with the 0-truncated objects in the $B G$-slice of $Singlrt \,\coloneqq\, Grpd_1^{cn}$:

$$G Orbt \;\simeq\; \left( (Grpd_1^{cn})_{/ B G} \right)_0 \,.$$

Under this identification, the adjunction is the canonical left base change on slices composed with the 0-truncation reflection (here):

That the right adjoint $R$ is fully faithful is most readily seen by direct inspection: A map between $\widehat{G}$-sets on both of which $\widehat{G}$ acts only through $G$ is evidently $\widehat{G}$-equivariant if and only if it is $G$-equivariant.

Related concepts

• orbit, orbit type

• equivariant homotopy theory

• global orbit category, global equivariant stable homotopy theory

• Bredon cohomology, equivariant cohomology

• topological G-space

• vector G-space

• equivariant dgc-algebra

• equivariant rational homotopy theory

References

The notion of the orbit category (for use in equivariant cohomology/Bredon cohomology) is due to

• Glen Bredon, Section I.3. of Equivariant cohomology theories, Springer Lecture Notes in Mathematics Vol. 34. 1967 (doi:10.1007/BFb0082690)

announced in

• Glen Bredon, Equivariant cohomology theories, Bull. Amer. Math. Soc. Volume 73, Number 2 (1967), 266-268. (educlid:1183528794)

and there considered specifically for finite groups.

Discussion for any topological group (and further generalization) is considered (together with the model category theoretic proof of Elmendorf's theorem) in:

• William Dwyer, Daniel Kan, Sec. 2.1 and Thm. 3.1 of: Singular functors and realization functors, Indagationes Mathematicae (Proceedings) Volume 87, Issue 2, 1984, Pages 147-153 (doi:10.1016/1385-7258(84)90016-7)

Textbook accounts:

• Tammo tom Dieck, Section I.10 of: Transformation Groups, de Gruyter 1987 (doi:10.1515/9783110858372)

• Wolfgang Lück, (8.16) in Transformation Groups and Algebraic K-Theory, Lecture Notes in Mathematics 1408 (Springer 1989) (doi:10.1007/BFb0083681)

• Peter May, Section I.4 of: Equivariant homotopy and cohomology theory CBMS Regional Conference Series in Mathematics, vol. 91, Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1996 (ISBN:978-0-8218-0319-6, pdf, pdf)

Lecture notes:

• Tammo tom Dieck, Section 1.3 of: Representation theory, 2009 (pdf)

For more in relation to global equivariant homotopy theory see

• Charles Rezk, Global Homotopy Theory and Cohesion

The notion of fundamental category of a $G$-space is due to

• tom Dieck 1987

• Lück 1989, 8.15

with further discussion in

• Dorette Pronk, Laura Scull, The Equivariant Fundamental Groupoid as an Orbifold Invariant, Homology, Homotopy and Applications 23 1 (2021) (arXiv:1908.01201, doi:10.4310/HHA.2021.v23.n1.a3)